A Gentle Introduction to Machine Learning with Pythonand Scikit-learn
一篇基于pthon和scikt-learn的关于机器学习的介绍
GuillermoMoncecchi, Diego Garat, Raúl Garreta
本文主要展现使用scikit-learn机器学习方法基本的使用。主要包括分类、回归和聚类,分类和聚类的数据集是使用1936年由Sir Ronald Fisher 引入的莺尾花数据,回归使用的是Boston 房屋数据。
设置环境
In [161]:
%pylab inline
Populating the interactive namespace from numpy and matplotlib
Import scikit-learn, numpy, scipy andpyplotIn [162]:
importnumpyasnp
importscipyassp
importmatplotlib.pyplotasplt
importsklearn
importIPython
importplatform
print ('Python version:', platform.python_version())
print ('IPython version:', IPython.__version__)
print ('numpy version:', np.__version__)
print ('scikit-learn version:', sklearn.__version__)
print ('matplotlib version:', matplotlib.__version__)
Python version: 3.3.5
IPython version: 3.2.0
numpy version: 1.9.2
scikit-learn version: 0.16.1
matplotlib version: 1.4.3数据集
每个sklearn的方法都对应有数据集,它引入一些大家耳熟能详的数据集合,比如莺尾花数据集合,包含了150组数据,三中类型,每组数据包含萼片的长度和宽度,花瓣的长度和宽度。
In [163]:
fromsklearnimport datasets
iris= datasets.load_iris()
X_iris= iris.data
y_iris= iris.target这份数据集合150*4,对于每组数据,我们有一个对应的分类。
In [164]:
print (X_iris.shape, y_iris.shape)
print ('Feature names:{0}'.format(iris.feature_names))
print ('Target classes:{0}'.format(iris.target_names))
print ('First instance features:{0}'.format(X_iris[0]))
(150, 4) (150,)
Feature names:['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
Target classes:['setosa' 'versicolor' 'virginica']
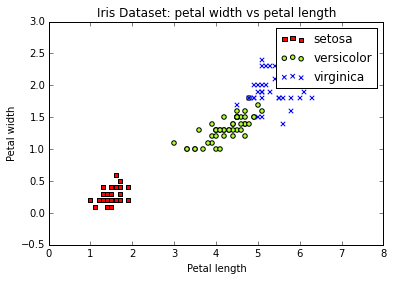
First instance features:[ 5.1 3.5 1.4 0.2]然后我们将数据打印出来,显示萼片,然后是花瓣数据。
In [212]:
plt.figure('sepal')
colormarkers= [ ['red','s'], ['greenyellow','o'], ['blue','x']]
for i inrange(len(colormarkers)):
px = X_iris[:, 0][y_iris== i]
py = X_iris[:, 1][y_iris== i]
plt.scatter(px, py, c=colormarkers[i][0], marker=colormarkers[i][1])
plt.title('Iris Dataset: Sepal width vs sepal length')
plt.legend(iris.target_names)
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.figure('petal')
for i inrange(len(colormarkers)):
px = X_iris[:, 2][y_iris== i]
py = X_iris[:, 3][y_iris== i]
plt.scatter(px, py, c=colormarkers[i][0], marker=colormarkers[i][1])
plt.title('Iris Dataset: petal width vs petal length')
plt.legend(iris.target_names)
plt.xlabel('Petal length')
plt.ylabel('Petal width')
plt.show()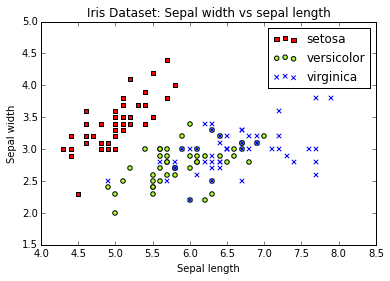
SupervisedLearning: Classification
1936年,Ronald Fisher引入莺尾花数据,使用他训练一条线性分类模型。构建一条特征的线性组合,即构造一条直线。
我们的任务是预测给定一份莺尾花萼片和花瓣长宽数据预测其类型。然后我们尝试只使用两个特征即萼片的长和宽。
常规的分类处理只要包括如下几步:
(1)特征选择
(2)基于可行数据构建模型
(3)对于测试数据评估模型效果
所以,在构建模型之前,我们应该将数据分为训练集和测试集,训练集将用于构建模型,测试集评估模型效果。.
Separatetraining and testing sets分离训练和测试数据集
我们第一步要做的就是分离数据集,75%为训练集,剩余的25%为测试集。同时,我们要做数据规范化,计算特征均值,每个特征和均值做差值,将结果除以标准差。规范化之后每维特征的均值为0.
In [213]:
fromsklearn.cross_validationimport train_test_split
fromsklearnimport preprocessing
# Create dataset with only the first two attributes
X, y = X_iris[:, [0,1]], y_iris# Test set will be the 25% taken randomly
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=33)
# Standarize the features
scaler= preprocessing.StandardScaler().fit(X_train)
X_train= scaler.transform(X_train)
X_test= scaler.transform(X_test)
Check that, after scaling, the mean is 0and the standard deviation is 1 (this should be exact in the training set, butonly approximated in the testing set, because we used the training set mediaand standard deviation):
In [214]:
print ('Training set mean:{:.2f} and standard deviation:{:.2f}'.format(np.average(X_train),np.std(X_train)))
print ('Testing set mean:{:.2f} and standard deviation:{:.2f}'.format(np.average(X_test),np.std(X_test)))
Training set mean:0.00 and standard deviation:1.00
Testing set mean:0.13 and standard deviation:0.71
Display the training data, after scaling.
In [215]:
colormarkers= [ ['red','s'], ['greenyellow','o'], ['blue','x']]
plt.figure('Training Data')
for i inrange(len(colormarkers)):
xs = X_train[:, 0][y_train== i]
ys = X_train[:, 1][y_train== i]
plt.scatter(xs, ys, c=colormarkers[i][0], marker=colormarkers[i][1])
plt.title('Training instances, after scaling')
plt.legend(iris.target_names)
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.show()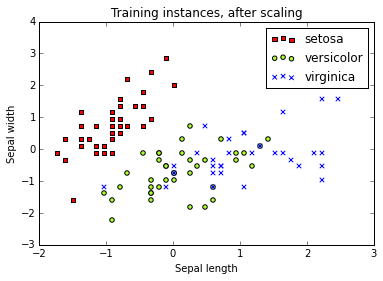
Alinear, binary classifier
首先,我们将问题转化成二分类问题,知识区别是否是setosa类型的花,只需要将非setosa类型的话的类型标识成一样的。
In [169]:
importcopy
y_train_setosa= copy.copy(y_train)
# Every 1 and 2 classes in the training set will became just 1
y_train_setosa[y_train_setosa>0]=1
y_test_setosa= copy.copy(y_test)
y_test_setosa[y_test_setosa>0]=1
print ('New training target classes:\n{0}'.format(y_train_setosa))
New training target classes:
[1 0 1 1 1 0 0 1 0 1 0 0 1 1 0 1 1 1 1 1 0 0 1 0 0 1 1 1 1 1 1 1 0 0 1 1 0
1 1 1 1 0 1 0 1 0 1 1 0 1 1 0 0 1 0 0 0 1 1 0 1 0 1 0 1 1 1 1 1 0 1 0 1 1
0 0 0 0 1 1 0 1 1 1 1 0 0 1 1 1 0 1 1 0 1 1 1 1 1 0 1 0 0 0 1 1 1 1 1 1 1
0]当前问题的分类是一个二分类,一条直线可以分隔开。
线性分类模型已有有了多年的研究,并且包含很多不同的方法来构建分类超平面。这里我们使用SGDClassifier的方法来构建线性模型,同时包好规范化。SGDClassifier分类模型如其名字使用了随机梯度下降的方法,一种计算函数局部最小值非常有效的方法。
梯度下降方法由Louis Cauchy在1847年提出,用来解线性方程组。这个思想基于多变量函数总是在它的负梯度方向下降最快。如果我们想得到它的最小值,我们可以在它的负梯度方向移动。
sklearn中的每个分类方法都使用的相同的模式,我们通过可配置参数调用一种分类方法,在这个例子中,我们使用 linear_model.SGDClassifier,来告诉sklearn使用对数损失函数。
In [170]:
fromsklearnimport linear_model
clf= linear_model.SGDClassifier(loss='log', random_state=42)
print (clf)
SGDClassifier(alpha=0.0001, average=False, class_weight=None, epsilon=0.1,
eta0=0.0, fit_intercept=True, l1_ratio=0.15,
learning_rate='optimal', loss='log', n_iter=5, n_jobs=1,
penalty='l2', power_t=0.5, random_state=42, shuffle=True, verbose=0,
warm_start=False)可以看出训练器包含几个变量。通常sklearn参数都有默认值。但是我们需要知道只使用默认参数不一定得到一个好的训练结果。
然后我们调用fit方法来训练分类器。
In [171]:
clf.fit(X_train, y_train_setosa)
Out[171]:
SGDClassifier(alpha=0.0001, average=False, class_weight=None, epsilon=0.1,
eta0=0.0, fit_intercept=True, l1_ratio=0.15,
learning_rate='optimal', loss='log', n_iter=5, n_jobs=1,
penalty='l2', power_t=0.5, random_state=42, shuffle=True, verbose=0,
warm_start=False)我们可以将分类器的系数打印出来。
In [172]:
print (clf.coef_,clf.intercept_)
[[ 30.97129662 -17.82969037]] [ 17.34844577]我们也可以把分类边界展现出来
In [173]:
x_min, x_max = X_train[:, 0].min()-.5, X_train[:, 0].max()+.5
y_min, y_max = X_train[:, 1].min()-.5, X_train[:, 1].max()+.5
xs= np.arange(x_min, x_max, 0.5)
fig,axes= plt.subplots()
axes.set_aspect('equal')
axes.set_title('Setosa classification')
axes.set_xlabel('Sepal length')
axes.set_ylabel('Sepal width')
axes.set_xlim(x_min, x_max)
axes.set_ylim(y_min, y_max)
plt.sca(axes)
plt.scatter(X_train[:,0][y_train==0], X_train[:, 1][y_train==0], c='red', marker='s')
plt.scatter(X_train[:,0][y_train==1], X_train[:, 1][y_train==1], c='black', marker='x')
ys= (-clf.intercept_[0]- xs * clf.coef_[0,0])/ clf.coef_[0,1]
plt.plot(xs, ys, hold=True)
plt.show()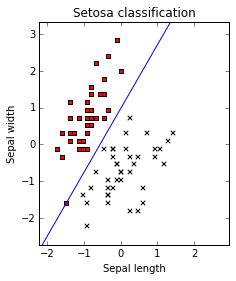
The blue line is our decision boundary. Every time 30.97×sepal_length−17.82×sepal_width−17.3430.97×sepal_length−17.82×sepal_width−17.34 isgreater than zero we will have an iris setosa (class 0).
Prediction预测
当我们有一个新的花,我们只需要知道它的花瓣的长和宽,然后调用predict方法来预测。我们所有机器学习的模型的预测都是直接调用predict,不管是任何分类方法或者任何方式构建的。
In [174]:
print ('If the flower has 4.7 petal width and 3.1 petal length is a {}'.format(
iris.target_names[clf.predict(scaler.transform([[4.7,3.1]]))]))If the flower has 4.7 petal width and 3.1 petal length is a [‘setosa’]
Note that we first scaled the newinstance, then applyied the predict method, and used the resultto lookup into the iris target names arrays.
Backto the original three-class problem回到三种类型的方法上
Now, do the training using the threeoriginal classes. Using scikit-learn this is simple: we do exactly the sameprocedure, using the original three target classes:
In [175]:
clf2= linear_model.SGDClassifier(loss='log', random_state=33)
clf2.fit(X_train, y_train)
print (len(clf2.coef_))三分类中sklearn将问题分解成三份二分类的子问题,如类型0可以线性分离出来,此时类型2和3是混在一起的。
In [176]:
x_min, x_max = X_train[:, 0].min()-.5, X_train[:, 0].max()+.5
y_min, y_max = X_train[:, 1].min()-.5, X_train[:, 1].max()+.5
xs= np.arange(x_min,x_max,0.5)
fig, axes = plt.subplots(1,3)
fig.set_size_inches(10,6)
for i in [0,1,2]:
axes[i].set_aspect('equal')
axes[i].set_title('Class '+ iris.target_names[i]+' versus the rest')
axes[i].set_xlabel('Sepal length')
axes[i].set_ylabel('Sepal width')
axes[i].set_xlim(x_min, x_max)
axes[i].set_ylim(y_min, y_max)
plt.sca(axes[i])
ys=(-clf2.intercept_[i]-xs*clf2.coef_[i,0])/clf2.coef_[i,1]
plt.plot(xs,ys,hold=True)
for j in [0,1,2]:
px = X_train[:, 0][y_train== j]
py = X_train[:, 1][y_train== j]
color = colormarkers[j][0]if j==ielse'black'
marker ='o'if j==ielse'x'
plt.scatter(px, py, c=color, marker=marker)
plt.show()Let us evaluate on the previous instanceto find the three-class prediction. Scikit-learn tries the three classifiers.
In [177]:
scaler.transform([[4.7,3.1]])
print(clf2.decision_function(scaler.transform([[4.7,3.1]])))
clf2.predict(scaler.transform([[4.7,3.1]]))
[[ 15.45793755 -1.60852842 -37.65225636]]
array([0])分类方法中可以得出分类模型的打分值。在例子中,第一个分类类型得出花朵是setosa,那么它就不回是另外两种花。如果得出的结果中有两个类型的都是整数,那么最大的scores值离分类线最远,那么我们选取最大的值作为预测类型。
Evaluatingthe classifier评估模型
评估模型用来评估分类算法的好坏,最常用的方法是准确率,给定一个分类器和一组类型数据,他将给出分类器预测值正确的比例。
In [178]:
fromsklearnimport metrics
y_train_pred= clf2.predict(X_train)
print ('Accuracy on the training set:{:.2f}'.format(metrics.accuracy_score(y_train, y_train_pred)))
Accuracy on the training set:0.83This means that our classifier correctlypredicts 83\% of the instances in the training set. But this is actually a badidea. The problem with the evaluating on the training set is that you havebuilt your model using this data, and it is possible that your model adjustsactually very well to them, but performs poorly in previously unseen data(which is its ultimate purpose). This phenomenon is called overfitting, and youwill see it once and again while you read this book. If you measure on yourtraining data, you will never detect overfitting. So, neverever measure on yourtraining data.
Remember we separated a portion of thetraining set? Now it is time to use it: since it was not used for training, weexpect it to give us and idead of how well our classifier performs onpreviously unseen data.
In [179]:
y_pred= clf2.predict(X_test)
print ('Accuracy on the training set:{:.2f}'.format(metrics.accuracy_score(y_test, y_pred)))
Accuracy on the training set:0.68一般情况下,测试集合上的准确率要低于训练集合,因为模型是基于训练集合训练的。
使用准确率的一个问题是不能反应模型在不同目标类型的效果。比如,我们知道我们的分类模型在setosa类型的花朵上效果很好,但是在分类其它两种类型是很有可能是失败的。所以如果我们同时衡量这些,对于我们提升效果、改变训练方法或者特征都很有效。
评估多分类中一种有效的方法是混淆矩阵。混淆矩阵中第i行的第j列的值是类型i被预测为类型j的示例数量。有了原始类型和预测类型,我们能很容易的打印混淆矩阵。
In [180]:
print (metrics.confusion_matrix(y_test, y_pred))
[[ 8 0 0]
[ 0 3 8]
[ 0 4 15]]通过打印出的矩阵,我们可以看出2行3列的数据8标识类型为1的花被预测为类型2,我们的分类器预测类型0的花朵效果很好,但是它在类型1和2上效果很差。混淆矩阵可以得到分类错误的很多有用信息。
Accuracy on the test set is a goodperformance measure when the number of instances of each class is similar,i.e., we have a uniform distribution of classes. However, consider that 99percent of your instances belong to just one class (you have a skewed): aclassifier that always predicts this majority class will have an excellentperformance in terms of accuracy, despite the fact that it is an extremelynaive method (and that it will surely fail in the “difficult” 1% cases).
Within scikit-learn, there are severalevaluation functions; we will show three popular ones: precision, recall, andF1-score (or f-measure).
In [181]:
print (metrics.classification_report(y_test, y_pred, target_names=iris.target_names))
precision recall f1-score support
setosa 1.00 1.00 1.00 8
versicolor 0.43 0.27 0.33 11
virginica 0.65 0.79 0.71 19
avg / total 0.66 0.68 0.66 38· Precision computes theproportion of instances predicted as positives that were correctly evaluated(it measures how right is our classifier when it says that an instance ispositive).准确率,样本中被预测为正样本的概率
· Recall counts the proportionof positive instances that were correctly evaluated (measuring how right ourclassifier is when faced with a positive instance).召回率:被预测为正样本的数据占全部正样本的概率。
· F1-score is the harmonic meanof precision and recall, and tries to combine both in a single number.F1值是准确率和召回率的调和均值,组合为一个单独的数值F1。
Usingthe four flower attributes使用莺尾花的4维数据
我们使用四维数据重复整个过程,检测它的效果是否有提升。
In [182]:
# Test set will be the 25% taken randomly
X_train4, X_test4, y_train4, y_test4 = train_test_split(X_iris, y_iris, test_size=0.25, random_state=33)
# Standarize the features
scaler= preprocessing.StandardScaler().fit(X_train4)
X_train4= scaler.transform(X_train4)
X_test4= scaler.transform(X_test4)
# Build the classifier
clf3= linear_model.SGDClassifier(loss='log', random_state=33)
clf3.fit(X_train4, y_train4)
# Evaluate the classifier on the evaluation set
y_pred4= clf3.predict(X_test4)
print (metrics.classification_report(y_test4, y_pred4, target_names=iris.target_names))
precision recall f1-score support
setosa 1.00 1.00 1.00 8
versicolor 0.78 0.64 0.70 11
virginica 0.81 0.89 0.85 19
avg / total 0.84 0.84 0.84 38
UnsupervisedLearning: Clustering
在有些情况下只得到没有标签的数据集,需要去探寻数据中隐藏的结构或者模式,前提是没有给定的目标分类或者评估模型,我们称这种机器学习任务是非监督的。聚类方法将数据集分组分成子集,在同一子集中的元素是相似的,和其它子集中的元素有差别。
K-means是最常用的距离算法,因为它简单且容易构建,并且在不同的任务上效果都很好。它属于分类算法将不同数据分类到不同组,即簇。
In [183]:
fromsklearnimport cluster
clf_sepal= cluster.KMeans(init='k-means++', n_clusters=3, random_state=33)
clf_sepal.fit(X_train4[:,0:2])
Out[183]:
KMeans(copy_x=True, init='k-means++', max_iter=300, n_clusters=3, n_init=10,
n_jobs=1, precompute_distances='auto', random_state=33, tol=0.0001,
verbose=0)
We can show the label assigned for eachinstance (note that this label is a cluster name, it has nothing to do with ouroriginal target classes... actually, when you are doing clustering you have notarget class!).
In [184]:
print (clf_sepal.labels_)
[1 0 1 1 1 0 0 1 0 2 0 0 1 2 0 2 1 2 1 0 0 1 1 0 0 2 0 1 2 2 1 1 0 0 2 1 0
1 1 2 1 0 2 0 1 0 2 2 0 2 1 0 0 1 0 0 0 2 1 0 1 0 1 0 1 2 1 1 1 0 1 0 2 1
0 0 0 0 2 2 0 1 1 2 1 0 0 1 1 1 0 1 1 0 2 1 2 1 2 0 2 0 0 0 1 1 2 1 1 1 2
0]Using NumPy’s indexing capabilities, wecan display the actual target classes for each cluster, just to compare thebuilt clusters with our flower type classes…
In [185]:
print (y_train4[clf_sepal.labels_==0])
[0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0]In [186]:
print (y_train4[clf_sepal.labels_==1])
[1 1 1 1 1 1 2 1 0 2 1 2 2 1 1 2 2 1 2 2 2 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1
2 1 2 1 1 2 1]
In [187]:
print (y_train4[clf_sepal.labels_==2])
[2 2 1 2 2 2 2 1 1 2 2 1 2 2 1 1 2 2 2 2 2 2 1 2 2]
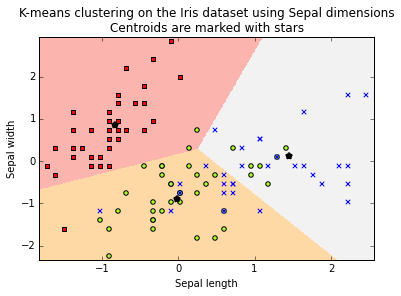
As usually, is a good idea to display ourinstances and the clusters they belong to, to have a first approximation to howwell our algorithm is behaving on our data:
In [188]:
colormarkers= [ ['red','s'], ['greenyellow','o'], ['blue','x']]
step=.01
margin=.1
sl_min, sl_max = X_train4[:, 0].min()-margin, X_train4[:, 0].max()+ margin
sw_min, sw_max = X_train4[:, 1].min()-margin, X_train4[:, 1].max()+ margin
sl, sw = np.meshgrid(
np.arange(sl_min, sl_max, step),
np.arange(sw_min, sw_max, step)
)
Zs= clf_sepal.predict(np.c_[sl.ravel(), sw.ravel()]).reshape(sl.shape)
centroids_s= clf_sepal.cluster_centers_
Display the data points and thecalculated regions
In [189]:
plt.figure(1)
plt.clf()
plt.imshow(Zs, interpolation='nearest', extent=(sl.min(), sl.max(), sw.min(), sw.max()), cmap= plt.cm.Pastel1, aspect='auto', origin='lower')
for j in [0,1,2]:
px = X_train4[:, 0][y_train== j]
py = X_train4[:, 1][y_train== j]
plt.scatter(px, py, c=colormarkers[j][0], marker= colormarkers[j][1])
plt.scatter(centroids_s[:,0], centroids_s[:, 1],marker='*',linewidths=3, color='black', zorder=10)
plt.title('K-means clustering on the Iris dataset using Sepal dimensions\nCentroids are marked with stars')
plt.xlim(sl_min, sl_max)
plt.ylim(sw_min, sw_max)
plt.xlabel("Sepal length")
plt.ylabel("Sepal width")
plt.show()
**Repeat the experiment, using petaldimensions**
In [190]:
clf_petal= cluster.KMeans(init='k-means++', n_clusters=3, random_state=33)
clf_petal.fit(X_train4[:,2:4])
Out[190]:
KMeans(copy_x=True, init='k-means++', max_iter=300, n_clusters=3, n_init=10,
n_jobs=1, precompute_distances='auto', random_state=33, tol=0.0001,
verbose=0)
In [191]:
print (y_train4[clf_petal.labels_==0])
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0]
In [192]:
print (y_train4[clf_petal.labels_==1])
[1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1
1]
In [193]:
print (y_train4[clf_petal.labels_==2])
[2 2 2 2 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 2 2 2 1 2 2 2 2]画出每一簇。
In [196]:
colormarkers= [ ['red','s'], ['greenyellow','o'], ['blue','x']]
step=.01
margin=.1
sl_min, sl_max = X_train4[:, 2].min()-margin, X_train4[:, 2].max()+ margin
sw_min, sw_max = X_train4[:, 3].min()-margin, X_train4[:, 3].max()+ margin
sl, sw = np.meshgrid(
np.arange(sl_min, sl_max, step),
np.arange(sw_min, sw_max, step),
)
Zs= clf_petal.predict(np.c_[sl.ravel(), sw.ravel()]).reshape(sl.shape)
centroids_s= clf_petal.cluster_centers_
plt.figure(1)
plt.clf()
plt.imshow(Zs, interpolation='nearest', extent=(sl.min(), sl.max(), sw.min(), sw.max()), cmap= plt.cm.Pastel1, aspect='auto', origin='lower')
for j in [0,1,2]:
px = X_train4[:, 2][y_train4== j]
py = X_train4[:, 3][y_train4== j]
plt.scatter(px, py, c=colormarkers[j][0], marker= colormarkers[j][1])
plt.scatter(centroids_s[:,0], centroids_s[:, 1],marker='*',linewidths=3, color='black', zorder=10)
plt.title('K-means clustering on the Iris dataset using Petal dimensions\nCentroids are marked with stars')
plt.xlim(sl_min, sl_max)
plt.ylim(sw_min, sw_max)
plt.xlabel("Petal length")
plt.ylabel("Petal width")
plt.show()
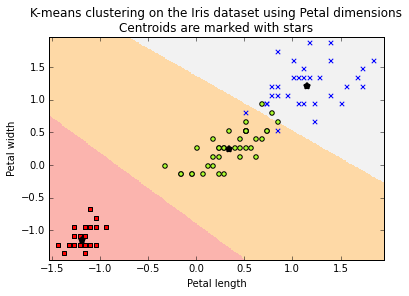
计算每一个簇
In [197]:
clf= cluster.KMeans(init='k-means++', n_clusters=3, random_state=33)
clf.fit(X_train4)
Out[197]:
KMeans(copy_x=True, init='k-means++', max_iter=300, n_clusters=3, n_init=10,
n_jobs=1, precompute_distances='auto', random_state=33, tol=0.0001,
verbose=0)In [198]:
print (y_train[clf.labels_==0])
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0]In [199]:
print (y_train[clf.labels_==1])
[1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 2 1 1 2 1]In [200]:
print (y_train[clf.labels_==2])
[2 2 1 2 2 1 2 2 1 2 2 2 1 2 1 2 2 2 1 2 2 2 2 2 1 1 2 2 2 2 2 2 2 1 2 2]Measure precision & recall in thetesting set, using all attributes, and using only petal measures
In [201]:
y_pred=clf.predict(X_test4)
print (metrics.classification_report(y_test, y_pred, target_names=['setosa','versicolor','virginica']))
precision recall f1-score support
setosa 1.00 1.00 1.00 8
versicolor 0.64 0.64 0.64 11
virginica 0.79 0.79 0.79 19
avg / total 0.79 0.79 0.79 38In [202]:
y_pred_petal=clf_petal.predict(X_test4[:,2:4])
print (metrics.classification_report(y_test, y_pred_petal, target_names=['setosa','versicolor','virginica']))
precision recall f1-score support
setosa 1.00 1.00 1.00 8
versicolor 0.85 1.00 0.92 11
virginica 1.00 0.89 0.94 19
avg / total 0.96 0.95 0.95 38Wait, every performance measure is betterusing just two attributes. It is possible that less features give betterresults? Although at a first glance this seems contradictory, we will see infuture notebooks that selecting the right subset of features, a process calledfeature selection, could actually improve the performance of our algorithms.
SupervisedLearning: Regression监督学习:回归
在上面的例子中我们可以看出我们的目标是预测非连续空间的类型。对于分类,集合是目标类,聚类中用于训练的数据集包含不同的计算集合。如果我们想得到一条线上的一个准确的数据,那么这就是一个回归问题。
我们使用经典的房屋价格的例子。
fromsklearn.datasetsimport load_boston
boston= load_boston()
print ('Boston dataset shape:{}'.format(boston.data.shape))
Boston dataset shape:(506, 13)
In [204]:
print (boston.feature_names)
['CRIM' 'ZN' 'INDUS' 'CHAS' 'NOX' 'RM' 'AGE' 'DIS' 'RAD' 'TAX' 'PTRATIO'
'B' 'LSTAT']
Create training and testing sets, andscale values, as usual
In [206]:
X_train_boston=boston.data
y_train_boston=boston.target
X_train_boston= preprocessing.StandardScaler().fit_transform(X_train_boston)
y_train_boston= preprocessing.StandardScaler().fit_transform(y_train_boston)创建一个训练和评估模型,这次评估中我们使用交叉验证。
交叉验证包含如下几步:
(1)将数据集分成k个不同的子集
(2)创建k个不同的模型,其中k-1个自己是训练集合,1个是测试集合
(3)计算k个模型的效果并使用均值作为结果。
In [207]:
deftrain_and_evaluate(clf, X_train, y_train, folds):
clf.fit(X_train, y_train)
print ('Score on training set: {:.2f}'.format(clf.score(X_train, y_train)))
#create a k-fold cross validation iterator of k=5 folds
cv = sklearn.cross_validation.KFold(X_train.shape[0], folds, shuffle=True, random_state=33)
scores = sklearn.cross_validation.cross_val_score(clf, X_train, y_train, cv=cv)
print ('Average score using {}-fold crossvalidation:{:.2f}'.format(folds,np.mean(scores)))交叉验证的主要优势是降低评估特征的方差,所以已有一份训练和测试集合,最终结果的将取决于构建这两份集合的方式。在机器学习中,普遍认为训练集和测试集的数据分类是均匀相似的,如果不均匀,则最终得到的结果是不准确的。交叉验证使我们降低这种风险,因为我们在k份不同的数据集上分别建立k个模型,然后取平均,这样我们会得到一个低方差且更加可信的模型。
sklearn有一个线性模型叫 linear_model.SGDRegressor ,它使用随机梯度下降来降低平方损失。
In [208]:
fromsklearnimport linear_model
clf_sgd= linear_model.SGDRegressor(loss='squared_loss', penalty=None, random_state=33)
train_and_evaluate(clf_sgd, X_train_boston, y_train_boston,5)
Score on training set: 0.73
Average score using 5-fold crossvalidation:0.70在分类中常使用准确率衡量模型效果,在回归中,我们预测真实值。在sklearn中默认的score方法为判定系数,用来衡量模型预测输出变量的概率。R2R2方法的结果从0到1,如果模型预测到所有的目标值则结果是最大值1.
In [209]:
print(clf_sgd.coef_)
[-0.06777406 0.06767528 -0.04290825 0.08828856 -0.11797833 0.3394894
-0.01969258 -0.23195707 0.09594823 -0.05271866 -0.19913907 0.10355794
-0.36852382]在上面的线性模型中我们调用penalty的参数为None,clf_sgd= linear_model.SGDRegressor(loss=’squared_loss’, penalty=None, random_state=33),则引入惩罚系数来避免过拟合,通过惩罚那些系统太大的超平面实现。这个参数默认是L2 或者L1,下面我们示例使用L2.
In [210]:
clf_sgd1= linear_model.SGDRegressor(loss='squared_loss', penalty='l2', random_state=33)
train_and_evaluate(clf_sgd1, X_train_boston, y_train_boston,folds=5)
Score on training set: 0.73
Average score using 5-fold crossvalidation:0.70Summary总结
结束这篇介绍,我们将总结sklearn中应用监督学习模型的主要通用步骤:
(1)数据集,选择你要训练的数据特征,并构造成二维数据,每行代表一个学习示例,每列标识一唯特征。每个特征由一个实数表示,但是数据原始可能不是这个样子。在真实环境中,这些预处理可能会花费一些时间。
(2)创建一个估计实例(分类器或者回归器)。在sklearn中,由fit和predict来建立实例,这个实例需要估计参数的模型,可以手动设置这些参数,也可以使用工具。
(3)分离训练和测试数据。
(4)使用fit(X,y)构建模型,其中x是训练数据,y是对应的分类。
(5)在测试集上评估模型效果,predict(T), T是测试集合
(6)和真实的目标分类比对。
这些步骤是一个复习,sklearn基于不同的机器学习操作还提供很多方法(比如降维、聚类、半监督学习),以及一些数据转换方法。

























 251
251











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








