卡尔曼滤波

系列文章目录

前言

一、线性高斯系统

二、卡尔曼滤波算法

1.卡尔曼滤波算法的应用

2.卡尔曼滤波的数学推导

1、预测部分的推导

2、观测部分的推导

---

前言

最近在阅读概率机器人这本书，读到了卡尔曼滤波的相关内容，想要记录下来以供以后的复习。对书中的内容进行了翻译并加入了自己的理解。在看之前大家可以先了解一下贝叶斯滤波算法的基本思想和基本的数学公式的推导。

---

一、线性高斯系统

卡尔曼滤波的使用场景是在线性系统中用于连续状态的预测的滤波算法。在某一时刻t，卡尔曼滤波的可信度是由两个参数来表示，分别是均值和协方差。满足一下三个性质以及贝叶斯滤波中的马尔可夫性质即满足卡尔曼滤波后验，可以进行状态的预测。

1、在添加加性高斯噪声之后状态转移概率函数必须是一个线性函数，其数学表达式如下：

其中和都是n维的状态向量(列向量)，是状态转移矩阵，是控制矩阵，是高斯噪声其均值是0，协方差矩阵是。把这个公式带入到高斯分布的概率密度函数中去可以得到以下公式：

2、在添加加性高斯噪声之后，其观测概率密度函数也必须是线性函数，其数学表达式如下：

 

同样带入高斯分布的概率密度函数中去可以得到

 

 下面这个图是卡尔曼滤波状态量和协方差矩阵的更新流程。

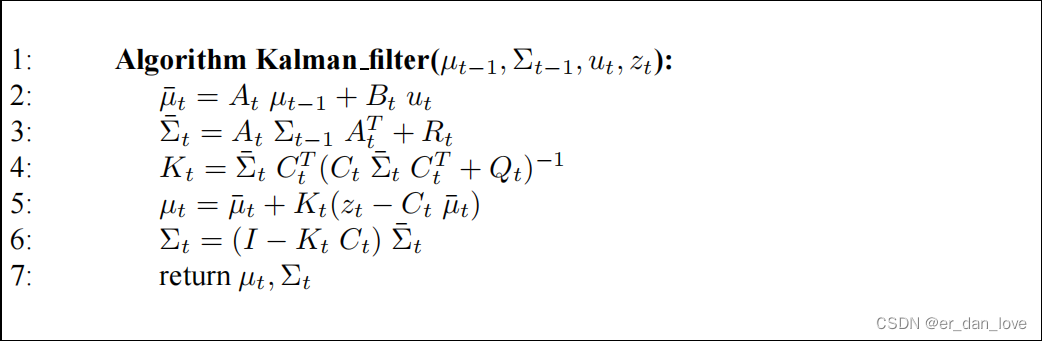
3、 初始的必须是正态分布(normal distributed)。其数学表示为：

 满足以上这三个性质，就能够确保是一个高斯分布。

二、卡尔曼滤波算法

1.卡尔曼滤波算法的应用

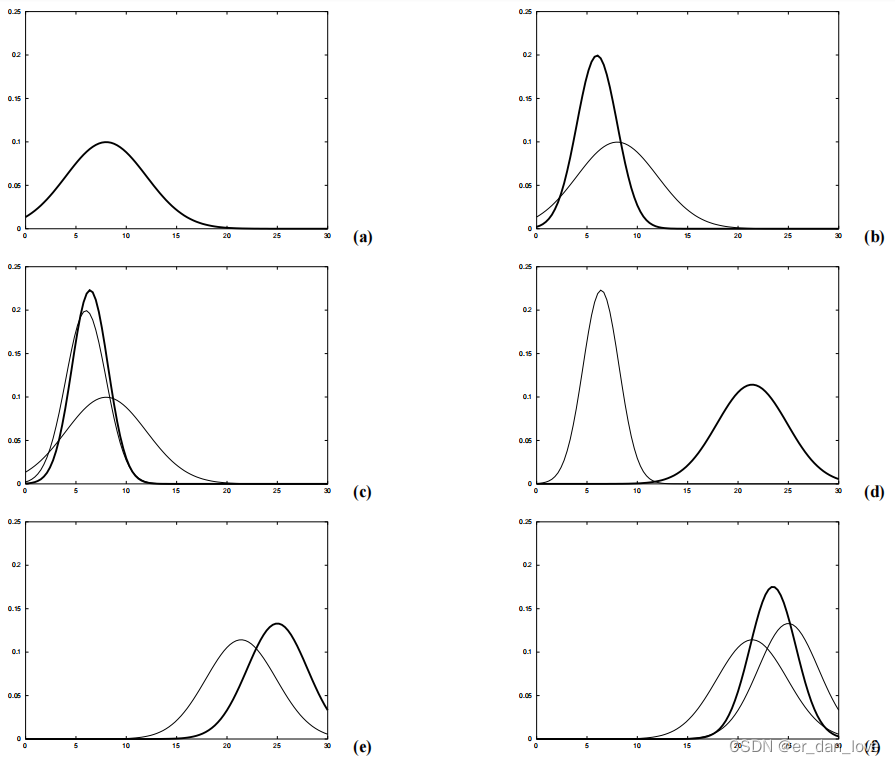
下图是一个卡尔曼滤波算法在一维上的简单的定位的应用。假设机器人沿着横轴移动。机器人的先验定位由高斯分布给出如图 (a)。通过机器人安装的传感器来返回一个它的位置信息如图(b)中的黑体线的峰值。其峰值是由传感器预测得到的，曲线的宽度表明了观测的不确定度，再结合先验的测量，如图(c)的粗体线是由先验以及传感器的测量得到的。可以看出来它的均值位于两条曲线的均值之间，且不确定度比之前两条曲线的不确定度都要小。

下一时刻，假设机器人向右移动，由于下一个状态的不确定性是随机的，它的不确定性会变大，所以会比较宽。如图(d)中的黑体曲线，然后在该时刻接受传感器的观测如图(e)中的黑体线。结合先验和测量信息可以得到如图(f)中的黑体线，同样可以看出该曲线的均值在两条曲线之间，且不确定性也减小。

 

2.卡尔曼滤波的数学推导

1、预测部分的推导

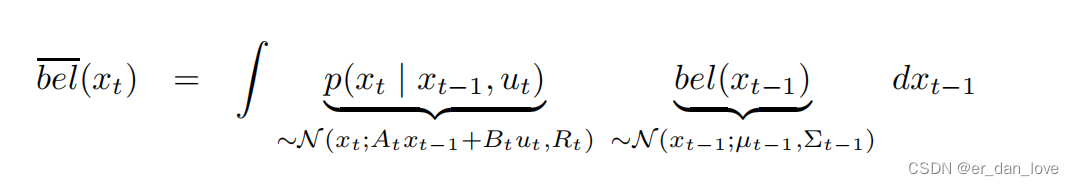
 的均值和方差分别是和，把这两个变量带入上面的公式可以得到下面这个公式：

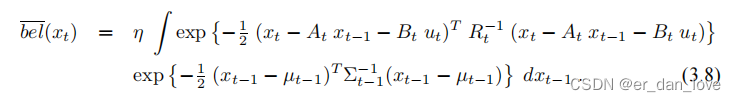
 为了看起来简单一些，记为

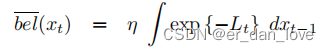
其中

 

 

现在把分解成两部分函数和，如下

 把这个变量全部集中在中，这样就可以把含有变量的项移出积分的外部，所以可以得到下面这个公式：

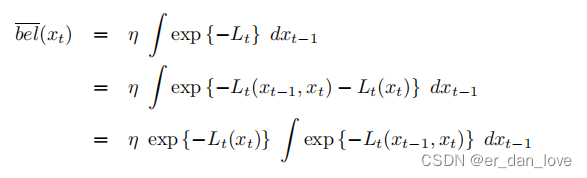
上式积分的值与无关，经过积分之后就可以得到：

 我们需要找到一个,关于的二次函数(这个二次函数中也会有,但是并不影响我们的求解)，为了确定这个函数，对求两次导数分别得到：

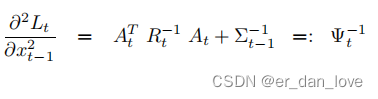
是函数的曲率，令一阶导数为0可以得到一个均值(注意我们是在求解),

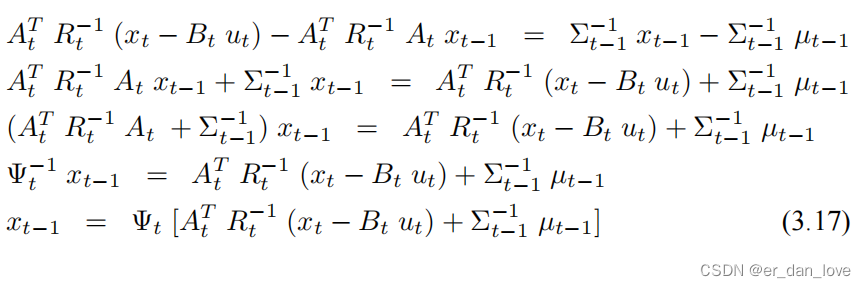 我们就可以得到一个二次函数如下所示：

 这个函数不是唯一的，事实上

是关于变量的高斯分布的密度函数，由概率密度函数的定义可得:

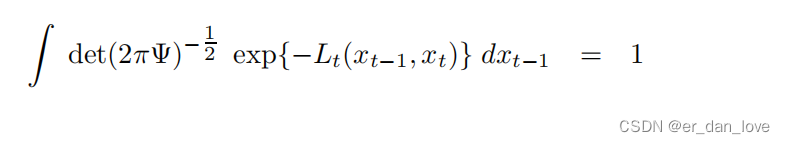
所以有：

由于积分的值和无关所以，可以得到如下的公式： 

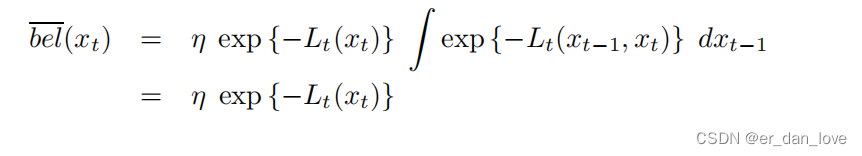
注意到等式两边的是不一样的，但是没有加以区分，在原书中有说明。接下来我们继续求解函数，注意到它和是不一样的，由之前的定义可以得到：

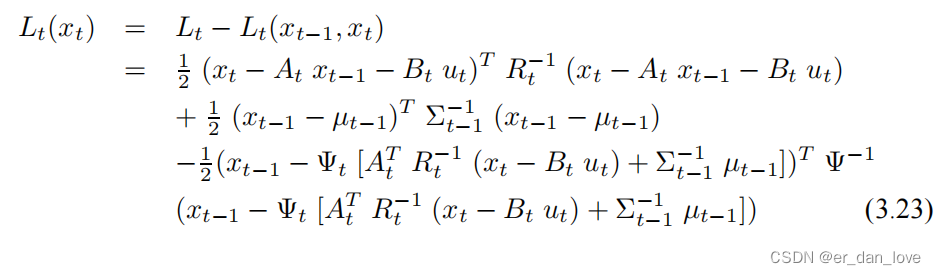
 将回带可以解得：

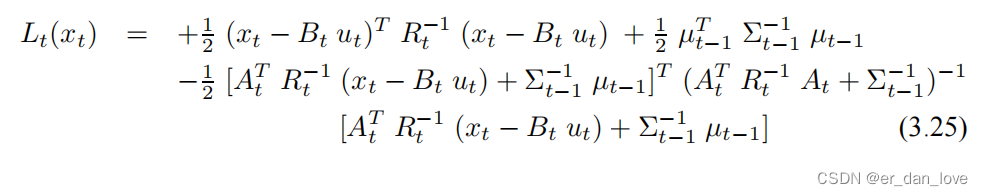
从上式中可以看出来与无关，且是关于的一个二次函数。也可以证明服从正态分布，对该函数分别求一阶导数和二阶导数可以得到均值和协方差。

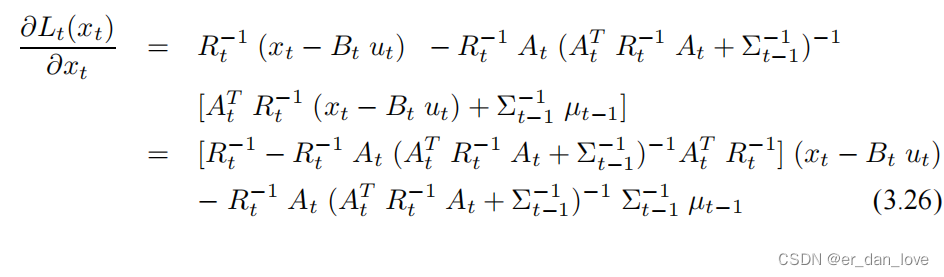
由 inversion lemma 定理可得：

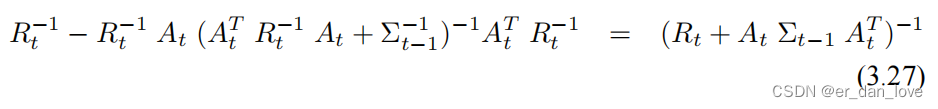
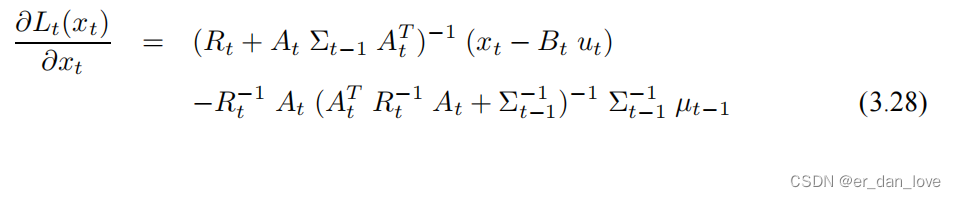
 令其一阶导数为零可以得到

 对其求二阶导数：

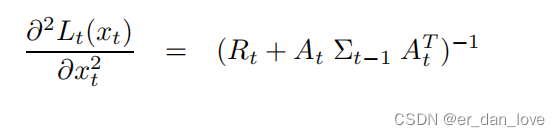
曲率的逆就是协方差矩阵。

2、观测部分的推导 

同样的从贝叶斯滤波出发有如下式子：

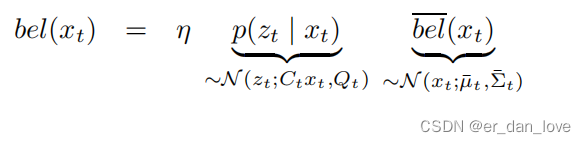
其中也服从正态分布，均值是，协方差是。故上式也可以表达为：

 其中

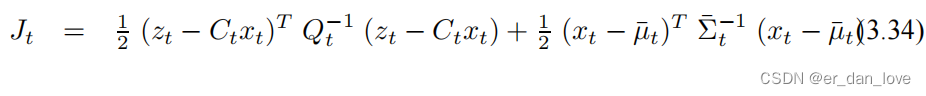
同样分别求一阶导数和二阶导数：

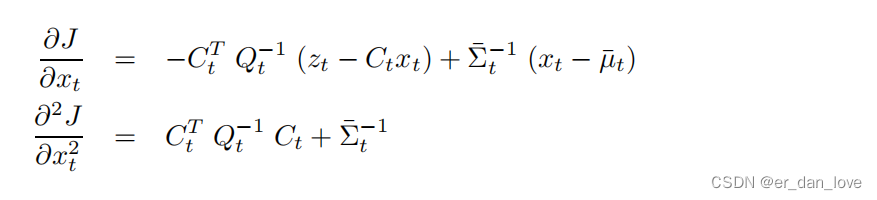
 对二阶导数取逆可以得到其协方差矩阵：

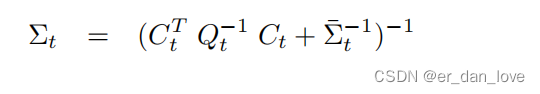
令一阶导数为0可以得到：

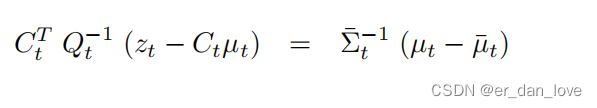
 上式的左侧可以写为：

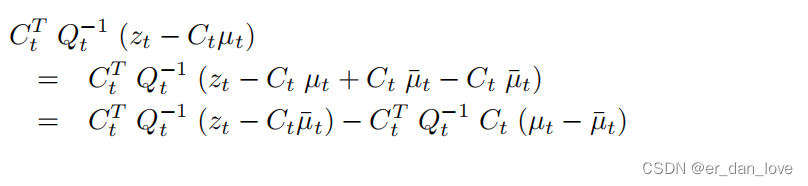
把上式带入上上式可以得到： 

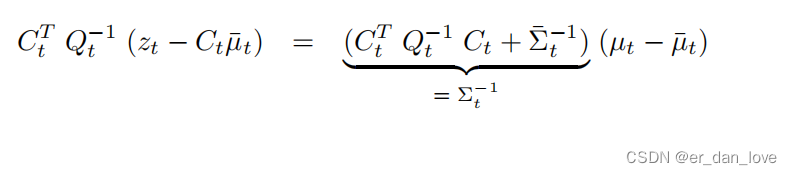 接下来就会得到一系列式子：

 定义K：

 

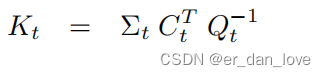
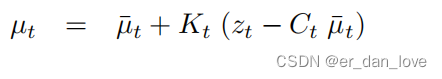
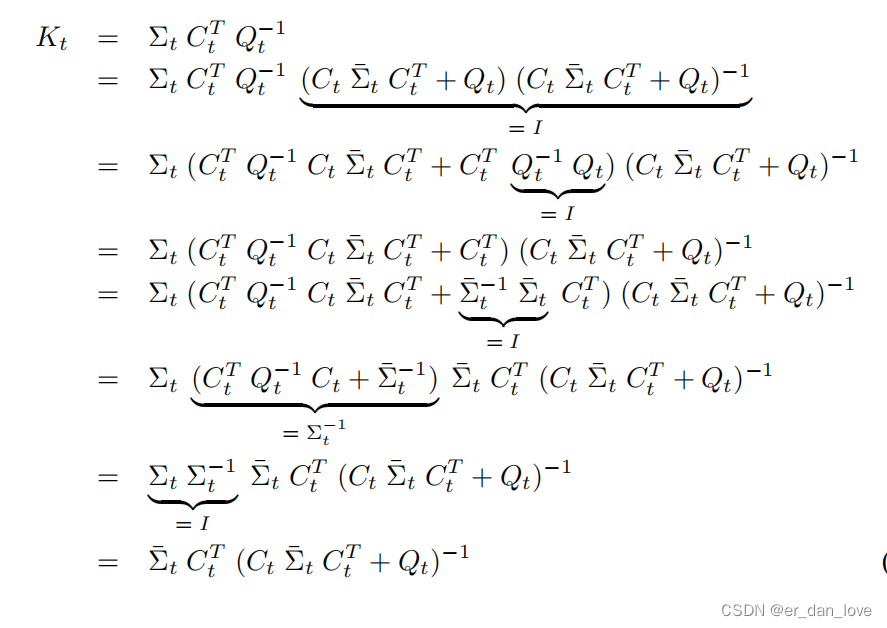
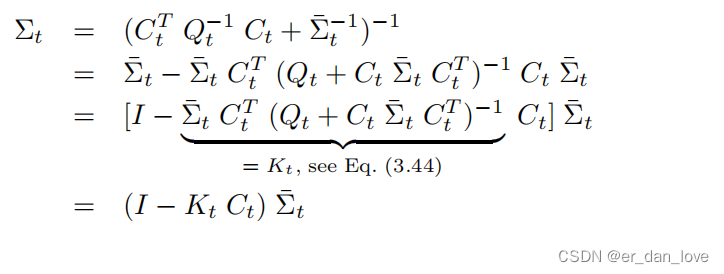
 到这里数学公式的推导就结束了。因为是第一次看所以肯定有不对的地方，大家可以一起讨论。图片来自概率机器人书籍。

---