smart3d的Omega，phi，kappa与旋转矩阵R及映射

smart3d的Omega，phi，kappa与旋转矩阵R及映射

Omega，phi，kappa

Smart3d的角元素与摄影测量书上的角元素有两点不同
1． 摄影测量中Phi角是顺时针的
2． Smart3D的z轴是朝下的，而摄影测量书上的z轴是朝上的（影响到phi，omega的大小（+或-PI）以及kappa角的正负）

omega相当于绕x轴逆时针旋转omega角
phi相当于绕y轴逆时针旋转phi角
kappa相当于绕z轴逆时针旋转kappa角

注意：角元素的单位一定要注意，到底是角度还是弧度一定要注意

经验证，在CGCS2000坐标系下的smart3d的坐标系的初始指向如图：

黑色坐标系为投影坐标系，即物方坐标系，蓝色为smart3d初始各轴的指向。

Ps：
逆时针：右手拇指与某个轴的指向相同，握拳的方向就是逆时针，绕某个轴逆时针转动可以想象成右手握住该轴，拇指指向与该轴相同并握拳。

旋转矩阵R

既然摄影测量书上的phi，omerga和kappa与smart3d上的角元素不同，那么就不能直接套用书上的公式了，下面就介绍怎么根据smart3d的导出的角元素计算旋转矩阵。

已经过验证：
这里以smart3D输出的phi，omerga和kappa为标准，旋转矩阵求法：

1. R是行优先，即：
   
2. R的计算：
   
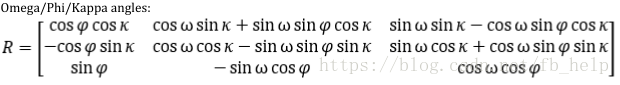
3. R的意义
   这里的R是由物方算到像方的，如果是像方算到物方需要R取逆，即转置。R和T定义了坐标系之间的转换（尺度一至）即，任意两笛卡尔坐标系可以通过R和T进行变换，这里的R是物方到像方的R即物方坐标系到像方坐标系的映射旋转矩阵。如果再已知T，就可以计算物方点的坐标，在像方坐标系（像空间坐标系）下的坐标。

小插曲

不同角度影像在物方某平面的投影：
omega = 0，phi =0，kappa=0

omega = 30°，phi =0，kappa=0

omega = 0，phi = 30°，kappa=0

omega = 30°，phi =30°，kappa=0

omega = 45°，phi =45°，kappa=0

产生如此图形的原因是，像片的一角超出了摄影中心所在的xy平面，导致有一角发生了“反投“，因为投影到地面上一平面，当有的点超出摄影时所在的平面S时，就会反投。
对比omega = 30°，phi =30°，kappa=0，前三个角都在平面S下，所有正常，只有一个角在S平面上，发生了反投。

物方到像方的映射

物方到像方的映射怎么算

由于普通相机拍摄时，是以x轴向右，y轴向上，z轴向上的方式进行摄像的，小孔成像的原理就是将现实世界投向屏幕，成倒立等大的像，它的坐标系的定义：一般x轴指向相片的右侧，y轴指向相片的上测，由右手系推知z轴指向相片的上面（指向摄影中心），但我们存储二维影像时是以x轴向上，y轴向下，的方式存储的。成像和存储之间必然不同，存在转换关系。

Smart3D的计算公式

详细介绍见smart3d用户手册camera model
Smart3d在像片平面，始终遵循x向左，y向下的标准，都是以此方式为基准。这种方式也是像片像素在内存中的存储的排列方式。后面称此坐标系为标准坐标系。

变换公式：

x = x0 + f*(mat.a1*(X - Xs) + mat.a2*(Y - Ys) + mat.a3*(Z - Zs)) / (mat.c1*(X - Xs) + mat.c2*(Y - Ys) + mat.c3*(Z - Zs));
y = y0 + f*(mat.b1*(X - Xs) + mat.b2*(Y - Ys) + mat.b3*(Z - Zs)) / (mat.c1*(X - Xs) + mat.c2*(Y - Ys) + mat.c3*(Z - Zs));

mat即为上面计算的旋转矩阵R；X，Y，Z是物方坐标，Xs，Ys，Zs是相机中心坐标；注意，这里的x0，y0指的是以标准坐标系下的x0，y0；
这样计算出来的x，y也是在标准坐标系下的x，y，可以直接存入影像。

另外C是相机在世界坐标系下的坐标。
世界点坐标转相机坐标：XCamera = R(Xworld-C)
而在计算机视觉中
世界点坐标转相机坐标：XCamera = RXworld+t
因此C！=t。
t=-RC，t是相机原点在世界坐标系下的坐标。