MATLAB仿真光的衍射（四）

圆孔衍射和艾里斑

显然整个成像系统（小孔，光源）都是圆对称的，在观察屏上的图样也应当是圆对称的。

圆孔衍射的推导在基础教育阶段不要求，可以直接带入已知公式

为了进一步了解艾里斑的图形，我们画出贝塞尔函数的图像

在matlab中内嵌有这个函数，可以直接调用。

clear
close all
upsilon = 0:0.01:15;
J1 = besselj(1,upsilon);
J2 = (2*besselj(1,upsilon)./upsilon).^2;
plot(upsilon,J1,upsilon,J2);
grid on
legend('J_1(\upsilon)','[2J_1(\upsilon)/\upsilon]^2')

结果：

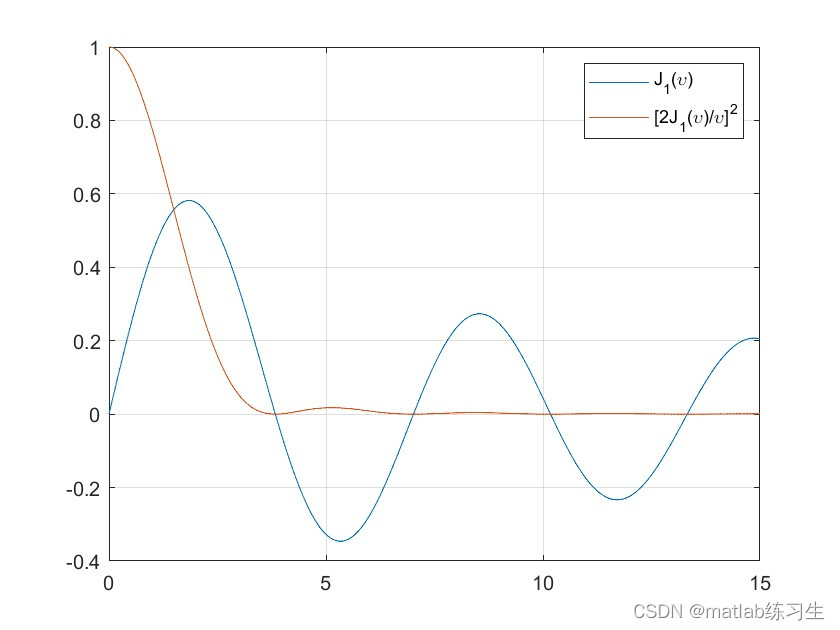
可以看出，对于贝塞尔函数，可以简单理解为带阻尼的正弦函数。 

同时，小孔衍射的结果，主要的光能量应当聚集在中央的亮条纹处。

利用求根函数可以求出上述函数的零点（精确）：

a = fzero(@(x)besselj(1,x),4)

得到艾里斑的暗条纹位置。
具体的小孔衍射程序代码如下：

lambda = 500e-9;
a1 = 0.5e-3;%小孔半径
a2 = 0.25e-3;
f = 0.2;%透镜焦距
H = 1e-3;%观察屏的尺寸
ScreenX = 500;
ScreenY = 500;

k = 2*pi/lambda;
y = linspace(-H/2,H/2,ScreenY);
x = linspace(-H/2,H/2,ScreenX);
[X Y] = meshgrid(x,y);
r =sqrt(X.^2+Y.^2);
theta = atan(r/f);
upsilon1 = 2*pi/lambda*a1*sin(theta);
upsilon2 = 2*pi/lambda*a2*sin(theta);
I1 = (2*besselj(1,upsilon1)./(upsilon1)).^2;
I2 = (2*besselj(1,upsilon2)./(upsilon2)).^2;

figure
subplot(1,2,1)
imshow(I1)
title(['a=' num2str(a1*1e3) 'mm']);
subplot(1,2,2)
imshow(I2)
title(['a=' num2str(a2*1e3) 'mm']);

结果：

可以看出，小孔的半径越小，艾里斑越大。
中央是明亮的，小孔衍射的能量主要集中在中央（零级衍射斑）。
 

思考以下问题，当两个艾里斑相互接近会发生什么呢？

当两个艾里斑相近时，可以用叠加原理计算共同的光强分布。

可以想象的是，两个点光源应当分别形成一个艾里斑，两个艾里斑相互靠近。

在相互靠近的过程中肉眼能看到的应当从两个光点逐渐合并成一个光点。

也就是说，在超越某个极限的时候，两个光点不能用肉眼区分，这就是我们说的分辨率的概念。
这里用代码仿真两个点光源的情况：

clear
close all
lambda = 500e-9;
a = 2e-3;%小孔半径
f = 2%观察屏距离
Hx = 3e-3;%观察屏的尺寸
Hy = 1e-3;%观察屏的尺寸
d = 1.22*lambda/(2*a)*f%两个艾里斑间距
ScreenX = 1500;
ScreenY = 500;
k = 2*pi/lambda;
y = linspace(-Hy/2,Hy/2,ScreenY);
x = linspace(-Hx/2,Hx/2,ScreenX);
[X Y] = meshgrid(x,y);
r1 =sqrt(X.^2+Y.^2);
r2 =sqrt((X-d).^2+Y.^2);
theta1 = atan(r1/f);
theta2 = atan(r2/f);
upsilon1 = 2*pi/lambda*a*sin(theta1);
upsilon2 = 2*pi/lambda*a*sin(theta2);
I1 = (2*besselj(1,upsilon1)./(upsilon1)).^2;
I2 = (2*besselj(1,upsilon2)./(upsilon2)).^2;

figure
subplot(2,1,1)
imshow(I1+I2)
subplot(2,1,2)
plot(x,I1(ScreenY/2,:)+I2(ScreenY/2,:));
hold on 
plot(x,I1(ScreenY/2,:),'k--',x,I2(ScreenY/2,:),'k--');
xlabel('x/m');
ylabel('相对光强')

结果：

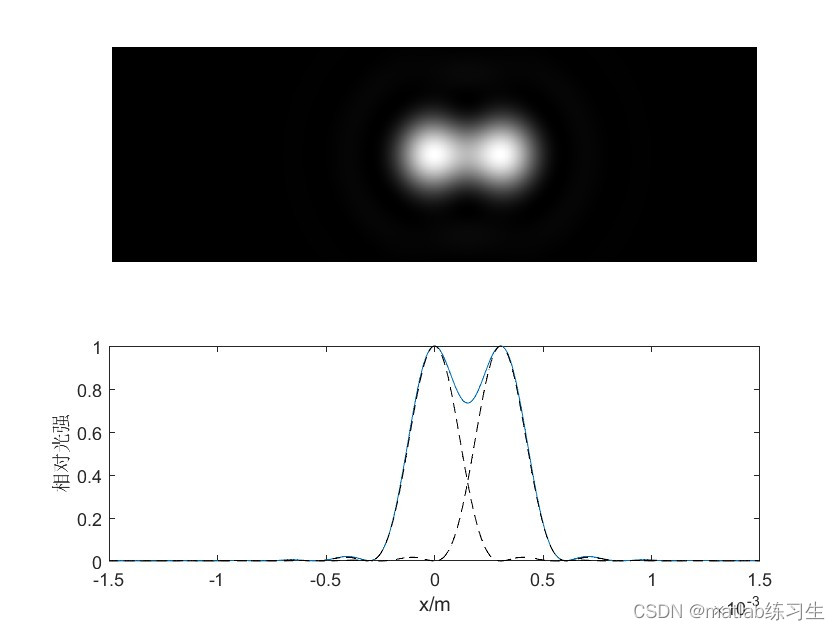
怎么理解这个代码呢？

我们使用X与（X-d）来区别两个相距d的点光源。

r1是相对（0,0）的距离，r2是相对（d,0）的距离。

在两个位置都有一个贝塞尔函数的函数（也就是艾里斑的分布函数）存在。

从中央位置的相对光强图可以看出光强的叠加形式。

当两个艾里斑靠近时，中央部分会变得模糊。
我们可以通过改变上述代码中间距的值来体现这一过程。
 

d2 = 1.0*lambda/(2*a)*f%两个艾里斑间距
d3 = 1.5*lambda/(2*a)*f%两个艾里斑间距

 

r2 =sqrt((X-d2).^2+Y.^2);
theta2 = atan(r2/f);
upsilon2 = 2*pi/lambda*a*sin(theta2);
I2 = (2*besselj(1,upsilon2)./(upsilon2)).^2;

figure
subplot(2,1,1)
imshow(I1+I2)
subplot(2,1,2)
plot(x,I1(ScreenY/2,:)+I2(ScreenY/2,:));
hold on 
plot(x,I1(ScreenY/2,:),'k--',x,I2(ScreenY/2,:),'k--');
xlabel('x/m');
ylabel('相对光强')

r2 =sqrt((X-d3).^2+Y.^2);
theta2 = atan(r2/f);
upsilon2 = 2*pi/lambda*a*sin(theta2);
I2 = (2*besselj(1,upsilon2)./(upsilon2)).^2;

figure
subplot(2,1,1)
imshow(I1+I2)
subplot(2,1,2)
plot(x,I1(ScreenY/2,:)+I2(ScreenY/2,:));
hold on 
plot(x,I1(ScreenY/2,:),'k--',x,I2(ScreenY/2,:),'k--');
xlabel('x/m');
ylabel('相对光强')

结果：

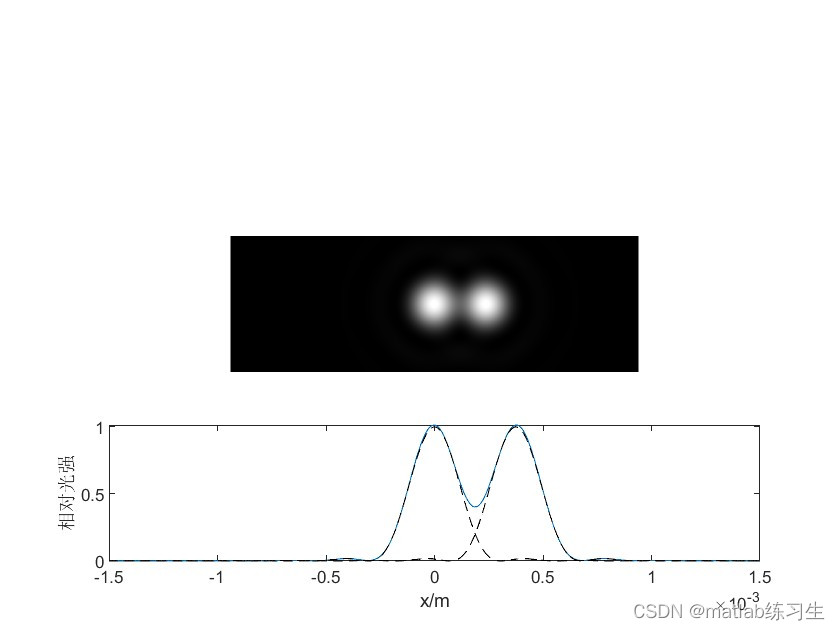
来源《高等光学仿真——光波导、激光》