【机器学习】ARIMA 在电商销售数据的分析应用

最新推荐文章于 2025-01-03 16:52:26 发布

风度78

最新推荐文章于 2025-01-03 16:52:26 发布

阅读量296

点赞数

原文链接：https://mp.weixin.qq.com/s?__biz=MzIwODI2NDkxNQ==&mid=2247522016&idx=2&sn=d0b9d927870401387844c0ffa141b642&chksm=960ba5921edcfff93adad031296450241e5cd99e2781f2c6035947011688807e0524f3c898e3&scene=126&sessionid=0

版权

一、引言

在带有时间序列性质的销售数据，可以帮助我们从历史销售数据中挖掘出潜在的模式和趋势，从而进行有效的预测。我们将介绍自回归积分滑动平均模型（ARIMA）在销售数据分析中的应用。

二、ARIMA 模型原理

自回归（AR）部分：ARIMA 模型中的自回归部分表示当前值与过去若干个值之间的线性关系。例如，一个阶自回归模型可以表示为，其中是时间的观测值，是常数项，是自回归系数，是过去个时间点的观测值，是误差项。
差分（I）部分：对于非平稳的时间序列数据，需要进行差分处理使其变为平稳序列。差分的次数决定了将原始数据进行几次差分才能达到平稳状态。例如，一阶差分表示。
滑动平均（MA）部分：滑动平均部分表示当前值与过去若干个误差项之间的线性关系。一个阶滑动平均模型可以表示为，其中是滑动平均系数，是过去个时间点的误差项。

三、分析过程

数据准备：收集历史销售数据，并进行数据清洗和预处理，包括处理缺失值、异常值等。
平稳性检验：使用单位根检验（如 ADF 检验）来判断时间序列数据是否平稳。如果数据不平稳，则需要进行差分处理，直到数据变为平稳序列。
模型定阶：通过观察自相关函数（ACF）和偏自相关函数（PACF）图，确定 ARIMA 模型的阶数、和。
模型拟合：使用确定的阶数对 ARIMA 模型进行拟合，得到模型参数。
模型诊断：检查模型的残差是否为白噪声，以确保模型的有效性。可以通过绘制残差的 ACF 和 PACF 图，以及进行Ljung-Box 检验来进行诊断。
预测：使用拟合好的模型对未来的销售数据进行预测。

四、案例应用

以某电商企业的月度销售数据为例，进行 ARIMA 模型的应用分析。

数据准备：收集了该企业过去两年的月度销售数据，共计 24 个观测值。经过数据清洗和预处理后，得到一个时间序列数据集。
平稳性检验：对原始销售数据进行 ADF 检验，结果显示数据不平稳。对数据进行一阶差分后，再次进行 ADF 检验，此时数据变为平稳序列。
模型定阶：观察一阶差分后数据的 ACF 和 PACF 图，初步确定 ARIMA 模型的阶数为，，。
模型拟合：使用确定的阶数对 ARIMA 模型进行拟合，得到模型参数如下：

常数项
自回归系数，
滑动平均系数

模型诊断：绘制模型残差的 ACF 和 PACF 图，发现残差在所有滞后阶数上都接近零，且 Ljung-Box 检验的值大于，表明残差为白噪声，模型有效。

预测：使用拟合好的模型对未来三个月的销售数据进行预测.

五、代码实现

!pip install statsmodels
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.tsa.arima_model import ARIMA

# 读取数据
data = pd.read_csv('/home/mw/project/sales_data.csv', index_col='date', parse_dates=True)

# 平稳性检验
from statsmodels.tsa.stattools import adfuller
result = adfuller(data['sales'])
print('ADF Statistic:', result[0])
print('p-value:', result[1])

# 差分处理
diff_data = data['sales'].diff().dropna()

# 模型定阶
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
plot_acf(diff_data)
plot_pacf(diff_data)
plt.show()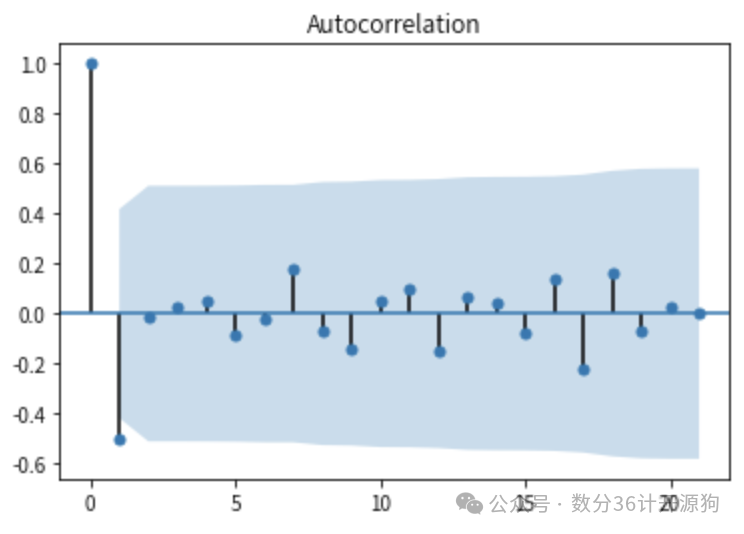

# 模型拟合
model = ARIMA(data['sales'], order=(2, 1, 1))
results = model.fit()

# 模型诊断
residuals = results.resid
plot_acf(residuals)
plot_pacf(residuals)
plt.show()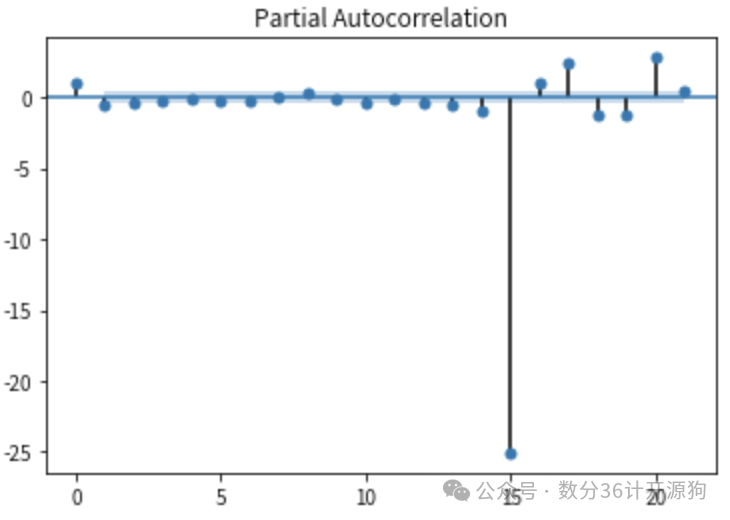

from statsmodels.stats.diagnostic import acorr_ljungbox
lb_test = acorr_ljungbox(residuals, lags=[10])
print('Ljung-Box test p-values:', lb_test[1])

# 预测
forecast = results.forecast(steps=3)
print('预测值:', forecast)

六、趋势分析

原始数据：绘制原始销售数据的时间序列图，观察数据的趋势和季节性特征。

plt.plot(data['sales'])
plt.title('原始销售数据')
plt.xlabel('时间')
plt.ylabel('销售额')
plt.show()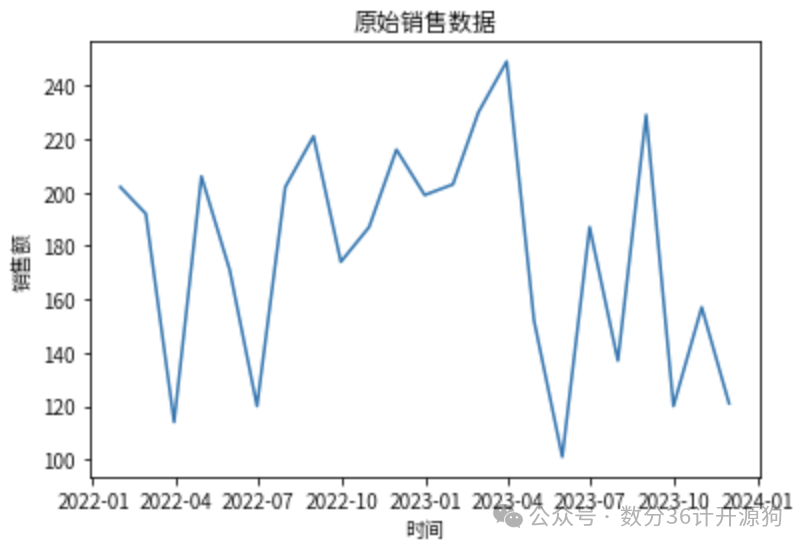

差分后数据：绘制一阶差分后数据的时间序列图，确认数据是否变为平稳序列。

plt.plot(diff_data)
plt.title('一阶差分后销售数据')
plt.xlabel('时间')
plt.ylabel('销售额差分')
plt.show()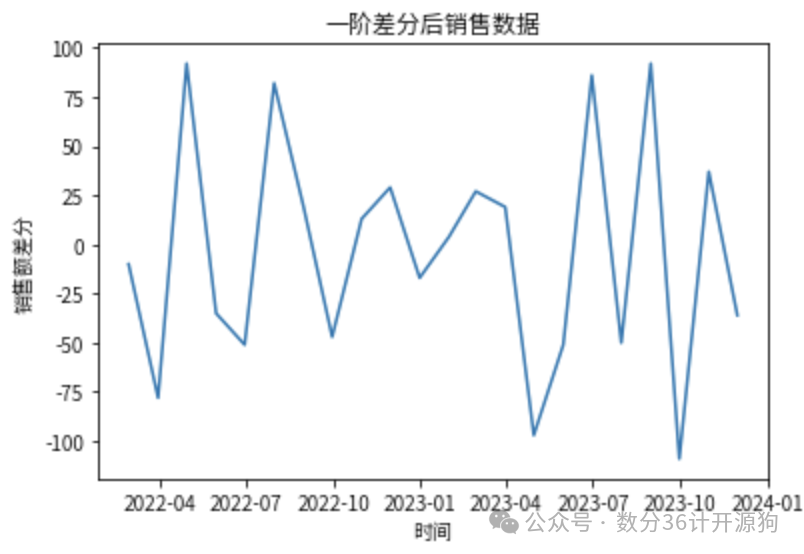

预测结果：将原始销售数据和预测值绘制在同一图中，直观展示预测效果。

# plt.plot(data['sales'], label='实际值')
plt.plot(pd.date_range(start=data.index[-1], periods=3, freq='M'), forecast[0], label='预测值')
plt.title('销售数据预测')
plt.xlabel('时间')
plt.ylabel('销售额')
plt.legend()
# plt.show()

七、结论

ARIMA 模型在销售数据分析中能够有效地捕捉时间序列数据中的趋势和季节性特征，进行准确的预测。

作者介绍：数分36计OpenDogs

往期精彩回顾




适合初学者入门人工智能的路线及资料下载(图文+视频)机器学习入门系列下载机器学习及深度学习笔记等资料打印《统计学习方法》的代码复现专辑

```
交流群
```

请备注：”昵称-学校/公司-研究方向“，例如：”张小明-浙大-CV“加群。

（也可以加入机器学习交流qq群772479961）