清华计算几何大作业（十）：CG2017 PA5-2 FruitNinja（水果忍者）· 上

1. 前置知识

1. 计算几何算法：1）Map Overlay，详见教材 2.3 计算子区域划分的叠合(2.3 Computing the Overlay of Two Subdivisions) 和 4.2 半平面求交 (4.2 Half-Plane Intersection) - 本章节主要讨论算法；2）4 线性规划：铸模制造 (Linear ProgrammingManufacturing with Molds) - 最优算法
2. DCEL
3. Duality，详见教材 8 排列与对偶：光线跟踪超采样(8 Arrangements and Duality Supersampling in Ray Tracing)
4. Segment Intersection，既 CG2017 PA1-2 Crossroad (十字路口) 所涉及的算法

这里给到必要观看的视频课程章节，这些内容对理解和实现 Half-Plane Intersection 算法至关重要，标记有绿色√为必看章节：

※ 视频课程仅介绍了Halfplane Intersetion，对于Linear Programming和Duality并在没有做过多讲解，大家可以参见教材。

2. 思路分析

问题描述：CG2017 PA5-2 FruitNinja（水果忍者）

2.1 解题思路

本题的突破口是题目提示的：

使用对偶（Duality）的方法，尝试将题目转换到对偶空间（Dual Plane）进行计算。

那么我们需要思考怎样进行对偶空间转换，才能求解题目的问题呢？首先，我们需要明确对偶空间转换的特点：

• 主平面（Primary Plane）中的点，在对偶平面中为直线；
• 主平面中的直线，在对偶平面中为点；

题目给到的输入数据是用端点表示的线段，那么我们现在有两种对偶转换的思路可供选择：

1. 将线段表示的直线转换成对偶空间中的点；
2. 将线段的两个端点转换成对偶空间中的直线；

我们先来看看第一种思路可行否？很遗憾这个思路不好使哦，因为在一般的对偶空间定义中，垂直线是没有定义的，对此感到疑惑的小伙伴可以看看下面直线在对偶空间中的定义：

l : y = mx + b - Primary Plane
l* := ( m, −b ) - Dual Plane

既然第一种方案不行，我们就来试试第二种方案吧！现在，线段的两个端点进行对偶空间转换后，我们会在对偶空间中得到两条直线：

而且我们知道在线段上的任意一点p3(x1, y3)，进行对偶空间转换后，会处于h1 和 h2的中间位置。假设我们将线段上所有的点都进行对偶空间转换，那么我们会得到一个平面空间区域（下图中的阴影区域）：

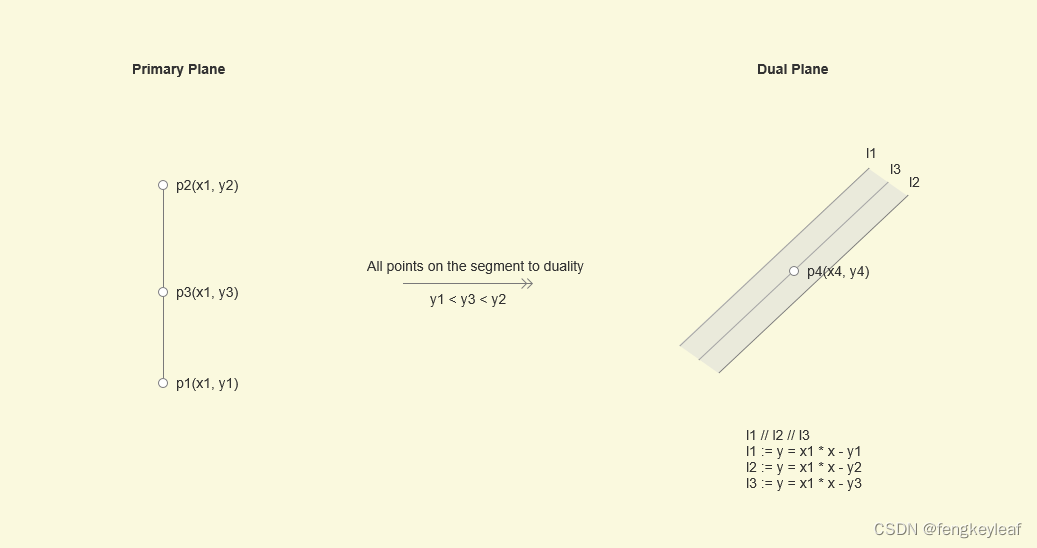
那么在对偶空间中，由两条边界直线所界定的平面区域中的任意一点p4(x4, y4)又有什么性质呢？根据笔者的观察，p4在转换到主平面之后，所形成的直线一定与线段有交点。我们线假设这个观察一定成立，那么可以得到这么一条有用的推论：

在对主平面中的垂直线段进行对偶空间转换*后，在对偶空间中得到的半平面会所界定出一个平面区域，如果该平面区域存在，则区域中任意一点转换到主平面的直线必然和每条垂直线段有交。

* 这里的对偶空间转换是指：两个线段端点所求得的半平面，而且这两个半平面相交的区域表示了在对偶空间的该线段。

到这里其实我们就得到了本题解题思路：先进性对偶空间转换，然后求得半平面相交的区域。但是！这一切都基于我们的观察假设，在进行具体的思路讲解之前，我们得先证明这个思路的正确性，即在对偶空间半平面相交区域中的任意一点，转换到主平面后的直线，一定和所有线段都有交点。

2.2 正确性证明（Correctness）

这里，笔者就用数学归纳法对之前的结论进行简要的证明。

首先，我们给到主平面线段在对偶空间的定义：
$$\begin{gathered} 线段s_1有两个端点p_1(x1,y1)和p_2(x1,y2)，y_1<y_2， \\ 他们所定义的对偶直线为l_1^{\ast }:=y=x_{1}x-y_1和l_2^{\ast }:=y=x_{1}x-y_2。s_1在对偶空间由两个半平面相交的区域表示： \\ R(x)=\{\begin{array}{ll}y-x_{1}x\le -y_1,& h1\\ y-x_{1}x\ge -y_2,& h2\end{array} \end{gathered}$$

给出定义以后，我们还需要简单证明一下半平面R(x)一定表示对偶空间中的线段s1：
$$\begin{gathered} 假设s_1上任意一点p_3(x1,y3),y1\le y2且y1\le y3\le y2，l_3^{\ast }:=y=x_{1}x-y_3 \\ 由y1\le y3\le y2可得：-y2\le -y3\le -y1，所以h2\le -y3\le h1=>h2\le y-x_{1}x\le h1 \\ 因此R(x)表示对偶空间中的s_1 \end{gathered}$$
接着我们就是使用数学归纳法进行证明，首先证明 n = 1 的情况：
当 n = 1 时，即线段集 S : = { s 1 } ，并且定义对应的对偶空间中的半平面集 H : = { h 1 , h 2 } , 以及 H 所定义的相交区域 R : = { h i ∩ h j ∣ h i ≠ h j , h i , h j ∈ H } 。 证明： ∀ p k ∗ : = ( x k , y k ) ∈ R ，这个点所对应的主平面直线 l k : = y = x k x − y k 与 S 中的所有线段有交点 我们先求 l k 与 s 1 所在直线 l 1 : = x = x 1 的交点： 联立两个直线方程，我们求得交点 p i : = ( x 1 , x k x 1 − y k ) ，并且由 p k ∗ ∈ R 可得： { x 1 x k − y k ≥ y 1 x 1 x k − y k ≤ y 2 所以 y 1 ≤ x 1 x k − y k ≤ y 2 ，即 p i ∈ s 1 ，证明完毕。 当 n = 1时，即线段集S := \{ s1 \}，并且定义对应的对偶空间中的半平面集H := \{ h1, h2 \}, 以及H所定义的相交区域R := \{ h_{i} \cap h_{j} | h_{i} \ne h_{j}, h_{i}, h_{j} \in H \}。 \\ 证明：{\forall} p_{k}^{*} := (x_{k}, y_{k}) \in R，这个点所对应的主平面直线 l_{k} := y = x_{k}x - y_{k}与S中的所有线段有交点 \\ 我们先求l_{k}与s1所在直线l_{1}:= x = x1的交点：\\ 联立两个直线方程，我们求得交点p_{i} := ( x_{1}, x_{k}x_{1} - y_{k})，并且由p_{k}^{*} \in R可得：\\ \begin{cases} x_{1}x_{k} - y_{k} \ge y_{1} \\ x_{1}x_{k} - y_{k} \le y_{2} \\ \end{cases} \\ 所以 y_{1} \le x_{1}x_{k} - y_{k} \le y_{2}，即 p_{i} \in s_{1}，证明完毕。 当n=1时，即线段集S:={s1}，并且定义对应的对偶空间中的半平面集H:={h1,h2},以及H所定义的相交区域R:={hi​∩hj​∣hi​=hj​,hi​,hj​∈H}。证明：∀pk∗​:=(xk​,yk​)∈R，这个点所对应的主平面直线lk​:=y=xk​x−yk​与S中的所有线段有交点我们先求lk​与s1所在直线l1​:=x=x1的交点：联立两个直线方程，我们求得交点pi​:=(x1​,xk​x1​−yk​)，并且由pk∗​∈R可得：{x1​xk​−yk​≥y1​x1​xk​−yk​≤y2​​所以y1​≤x1​xk​−yk​≤y2​，即pi​∈s1​，证明完毕。

接下来我们假设 n = k 时成立，证明 n = k + 1 时也成立：
假设 n = k 时成立，即 S : = { s 1 , . . . . , s k } , H : = { h 1 , h 2 , . . . , h 2 k + 1 , k 2 k + 2 } , R : = { h i ∩ h j ∣ h i ≠ h j , h i , h j ∈ H } 。 并且 ∀ p m ∗ : = ( x m , y m ) ∈ R ，这个点所对应的主平面直线 l m : = y = x m x − y m 与 S 中的所有线段有交点 证明：当 n = k + 1 时也成立，即 S ′ : = S ∪ s k + 1 ， H ′ : = H ∪ { h 2 k + 3 , h 2 k + 4 } ， R ′ : = R ∩ { h 2 k + 3 ∩ h 2 k + 4 } ， ∀ p n ∗ : = ( x n , y n ) ∈ R ′ ，这个点所对应的主平面直线 l n : = y = x n x − y n 与 S ′ 中的所有线段有交点 我们知道 R ′ ∈ R ，所以 l n 与 S 中的所有线段相交，现在仅需证明 l n 与 s k + 1 相交即可 而且该证明过程和 n = 1 时一模一样，这里不再赘述，证明完毕。 假设 n = k 时成立，即 S := \{ s_{1}, ...., s_{k} \}, H := \{ h_{1}, h_{2}, ..., h_{2k+1}, k_{2k+2}\}, R := \{ h_{i} \cap h_{j} | h_{i} \ne h_{j}, h_{i}, h_{j} \in H \}。\\ 并且{\forall} p_{m}^{*} := (x_{m}, y_{m}) \in R，这个点所对应的主平面直线 l_{m} := y = x_{m}x - y_{m}与S中的所有线段有交点 \\ 证明：当 n = k + 1 时也成立，即 S' := S \cup s_{k+1}，H':= H \cup \{ h_{2k+3}, h_{2k+4} \}，R' := R \cap \{ h_{2k+3} \cap h_{2k+4} \}，\\ {\forall} p_{n}^{*} := (x_{n}, y_{n}) \in R'，这个点所对应的主平面直线 l_{n} := y = x_{n}x - y_{n}与S'中的所有线段有交点 \\ 我们知道 R' \in R，所以 l_{n} 与 S 中的所有线段相交，现在仅需证明l_{n}与s_{k+1}相交即可 \\ 而且该证明过程和 n = 1 时 一模一样，这里不再赘述，证明完毕。 假设n=k时成立，即S:={s1​,....,sk​},H:={h1​,h2​,...,h2k+1​,k2k+2​},R:={hi​∩hj​∣hi​=hj​,hi​,hj​∈H}。并且∀pm∗​:=(xm​,ym​)∈R，这个点所对应的主平面直线lm​:=y=xm​x−ym​与S中的所有线段有交点证明：当n=k+1时也成立，即S′:=S∪sk+1​，H′:=H∪{h2k+3​,h2k+4​}，R′:=R∩{h2k+3​∩h2k+4​}，∀pn∗​:=(xn​,yn​)∈R′，这个点所对应的主平面直线ln​:=y=xn​x−yn​与S′中的所有线段有交点我们知道R′∈R，所以ln​与S中的所有线段相交，现在仅需证明ln​与sk+1​相交即可而且该证明过程和n=1时一模一样，这里不再赘述，证明完毕。
到此我们完成了解题思路的证明，接下来我们就把重点放在具体的实现思路上面。

---

上一节：CG2017 PA2-2 Find Dancing Partners (寻找舞伴) · 下

下一节：CG2017 PA5-2 FruitNinja（水果忍者）· 下

系列汇总：清华计算几何大作业思路分析和代码实现

3. 参考资料

1. Computational Geometry: Algorithms and Applications
2. 计算几何 ⎯⎯ 算法与应用, 邓俊辉译，清华大学出版社
3. 计算几何 | Computational Geometry

4. 免责声明

※ 本文之中如有错误和不准确的地方，欢迎大家指正哒~
※ 此项目仅用于学习交流，请不要用于任何形式的商用用途，谢谢呢；

---