清华计算几何大作业（十）：CG2017 PA5-2 FruitNinja（水果忍者）· 下

2. 思路分析

2.3 Linear Programming

根据上一节的思路，我们只需要在对偶空间里面求解Half-plane Intersection即可，但是我们需要注意一下题目所需要求解的问题：题目需要我们求解是否有解，而不是整个空间解集。也就说我们可以把求解整个空间解集转换成求其中一个解，只要有一个解，我们就能回答题目有没有的问题，也能简化求解的复杂度。

因为原先我们是求解空间平面，现在我们只是求解一个点，大大降低算法难度。依据这个思路，我们直接使用教材上面的Linear Programming（LP）就可以解决问题。这个方法非常的直接，这里使用教材上面的图例¹简要说明一下，大家就能看图理解啦哒：

但是这个方法有较高的数学浓度！Linear Programming具体有两种求解方法：1）有界LP 或 2）无界LP；前者需要根据实际问题确定角点，后者需要先判断一个矢量→d，判别方法教材中有涉及，但笔者数学功力不太行，实在无法理解，所以也无法实现这个解法。但是这个方法是本题的最优解，根据教材上面的定理：

〖定理4.10〗¹
即使是在最坏情况下，使用不超过线性规模的空间，也可以在O(n)的随机期望运行时间内，对包含n 个约束条件的任何二维线性规划问题进行求解。

我们可以得到这个方法的时间和空间复杂度都为O( 2n )，因为最多有2n个端点，也即有线性数量的半平面，所以这个解法为理论上的最快算法。因为没有实现，所以这里笔者把实现细节的分享放在后一种方法，直接求解整个解集空间：Half-plane Intersection。如有童鞋成功实现这个方法，请务必联系我拜膜一下哇~

2.4 Half-plane Intersection

2.4.1 整体思路

Half-plane Intersection算法是基于 Map Overlay，所以在阅读下面内容之前，大家需要理解Map Overla算法。Half-plane Intersection算法非常的直接，使用的是Divide-and-Conquer（分治）进行计算，每次递归返回时，我们需要使用MapOverlay来计算半平面的交集（这个交集必为Covexll），但这个交集和之前的MapOverlay不太一样，这里的交集结果可能是平面，线段，或者是点。

而且实现起来最为棘手的问题是，半平面理论上是一个无限大的平面，而MapOverlay处理的是有限的平面。笔者尝试直接使用半平面来求解，但实在是太复杂，最后遂放弃。之后只能祭出计算几何里面的一个”大杀器“：无限化有限，即我们最开始用一个Bounding box把所有半平面转换成有限的平面，然后再用MapOverlay进行求解即可：

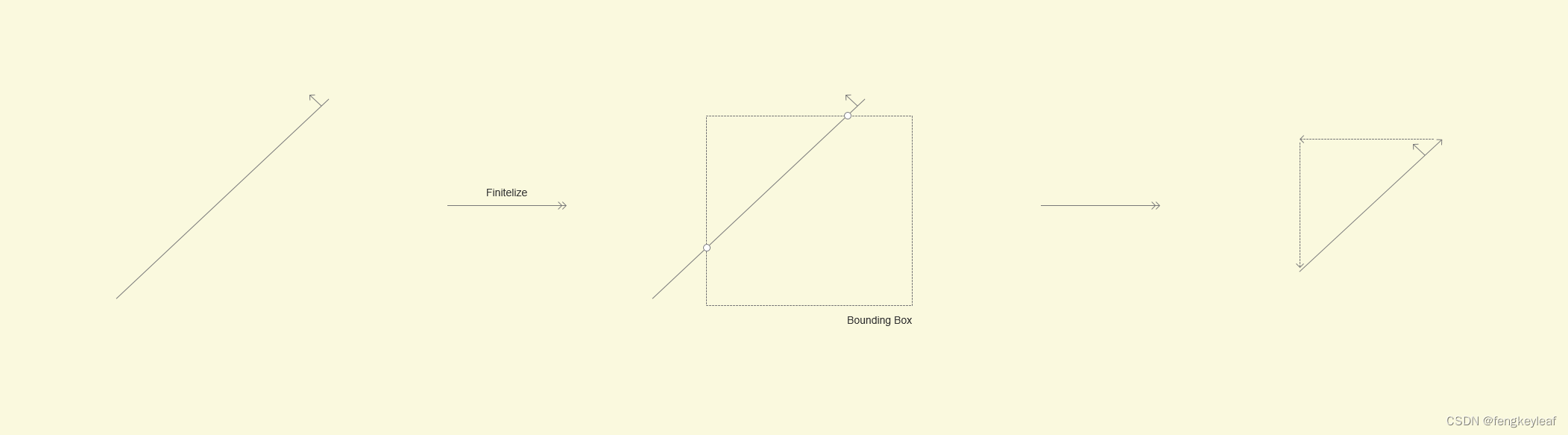
和CG2017 PA1-2 Crossroad (十字路口)处理思路类似，但是这样也会遇到一个相同的问题：我们怎么选定一个足够大的 Bounding Box 能覆盖所有的半平面的相交区域呢？笔者想了半天只能先找出所有半平面的交点，然后用一个能覆盖所有交点的 Box 来进行计算，但是这样又会有一个问题：我们如何在O( nlogn )时间内求得相当于n条直线的交点呢？而且这个方法还不能覆盖没有交点的情况，即所有半平面所在的直线都是平行的。所以这个问题也是一个实际实现之中遇到的难度，最后的解决方法是用一个数值很大的 Box 来进行求解，虽然能满足题目上面的数据集，但在理论上还是有缺陷。如果大家对此有比较好的思路，欢迎讨论哒~

解决了半平面的无限化问题，接下来就是如何进行求交计算了。总的来说，笔者总结了Haff-plane Intersection之中所涉及的相交情况，因为相交结果只有四种：有限平面，线段，点，空集。那么我们需要考虑的相交情况，就是上述四种结果的排列组合。这里我们简要说明一下每种情况的求解方法：

1. 点 & 点：只需要判断两个点是否重合，重合则有解，且解为点；如果不重合，则解为空；
2. 点 & 线段：只需判断点是否在线段上面，在则解为点；如果不在，则解为空；
3. 点 & 面：只需判断点是否在面之中（或边界上），在则解为点；如果不在，则解为空；
4. 线段 & 线段：线段稍微复杂一些，解可能为点，线段；
5. 线段 & 面：同样解可能为点，线段；
6. 面 & 面：使用MapOverlay求解即可，再查看两个平面是否有相交的面，有则输出该面，如果相交于一点，则解为点，如果相交为线段，则解为线段；
7. 空集 & ( 点 | 线段 | 面 | 空集 ) ：只要有一个为空，结果必为空集；

有限平面相交，笔者在MapOverlay里面已经进行过详细介绍，这里就不再赘述，所以我们把重点放在4）和 5）上面，而且两者有相似的地方。

2.4.2 线段和面的相交

首先，我们先来看看线段 & 线段求交结果的所有情况：（注意这里不是一般的线段求交，解可能为线段）

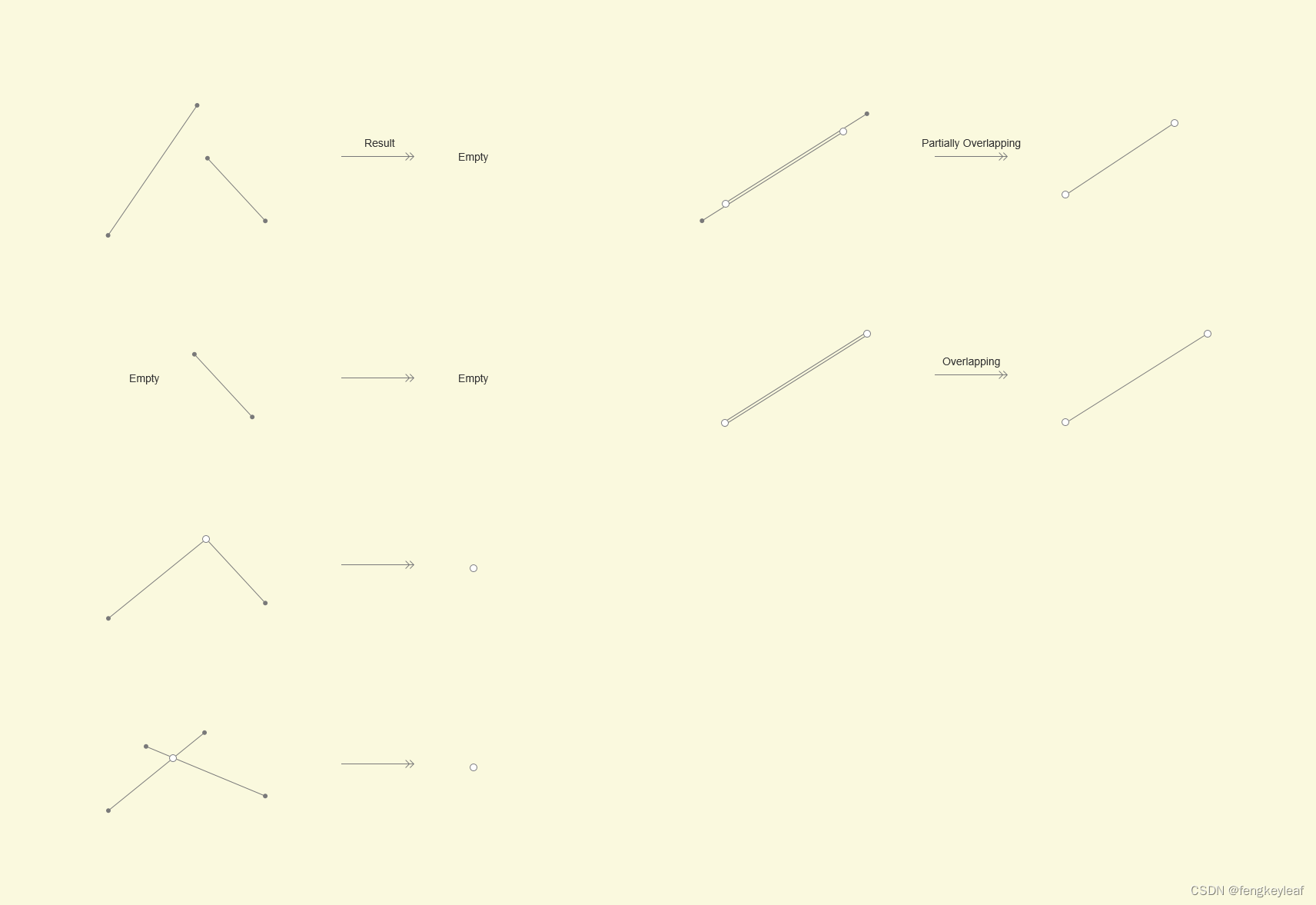
我们可以观察到，两条线段1）如果没有交点，则解为空；2）如果有一个交点，则解为交点；3）如果有两个交点，则解为两个交点组成的线段。通过这个观察，我们可以使用Segment Intersection算法进行求解，根据交点的数目来求得具体的解。但是，这里用到的Segment Intersection算法需要报告重合线段的交点，但之前一般意义上来说，这种不算相交，但这里需要报告出来，需要大家注意。

接下来，我们来看看线段和面相交的所有情况：

和线段 & 线段类似，我们还是先通过交点的数目来进行判断，但情况会复杂很多：

1. 如果没有交点，且两个端点都不在平面内，则解为空；但如果两个端点都在平面内，则解为线段；
2. 如果有一个交点，且有一端端点在平面内部，则解为交点后在平面内部端点所组成的线段；如果没有端点落在平面内，则解为交点；
3. 如果有两个交点，则解为两个交点组成的线段；

所以我们可以先把平面转换成线段（组成平面的线段），然后与给定线段进行Segment Intersection算法求点交，之后再根据上述情况分情况进行讨论即可，但要注意平面线段自己的交点不需要报告。并且图例中我们使用的三角形，但任意凸多边形都有相似的性质。并且根据教材上面的定理：

〖推论4.4〗¹
给定平面上的一组共n 张半平面，可以使用线性的空间，在O(nlogn)时间内计算出其公共的交集。

我们可知，这个解法的时间复杂度为O( nlogn )，但说实话，这个解法实现难度超高，因为需要另外两个算法（Segment Intersection & MapOverlay ）作为基础算法，才能进行实现，所以不太推荐Half-plane Intersection去解决本题。大家可以看看 2.5 其他解法 中的其他思路。

到此我们讲解完Half-plane Intersection的实现细节，同时在这里我们也全部实现和讲解了 清华计算几何 10个大作业，不知道大家一路看下来，觉得难度如何？是不是既折磨又享受哒？哈哈，也感谢大家一路以来的支持咯，能看到这里真是辛苦了呢~~之后应该会把重心转向找工和个人网站的搭建上面了，再像现在这样无忧无虑的搞研究的机会可能不多了呢。

最后在这里感叹一句哒：这个过程真的是，很开心哦~ 那么，暂时拜拜咯ヾ(•ω•`)o

2.5 其他解法

根据 @IIIustrious 的思路，本题可以利用凸包算法来解决，具体思路如下：

数据点筛选：

​ 数据点存在以下问题，需要经过处理才能使用。

1. 有的线段横坐标相同
2. 给定线段的纵坐标顺序混乱
3. 线段的两个端点同时存储在一个三元组里。

​ 针对以上问题，需要特殊处理数据：

1. 同一横坐标有多条直线的，只保留一对端点，下端点取所有下端点中最高的，上端点取所有上端点中最小的
2. 在输入时判断两个纵坐标大小，看情况swap一下
3. 上点和下点分开存储，放在数组里

求半凸包：

​ 需要求上下端点的半凸包，这里封装了Andrew算法求半凸包：先横坐标排序再Graham Scan。

线性扫描求交：

​ 需要判断上下半凸包是否有交，有交一般来说就是没有直线能通过。有交但是能通过一条直线时需要特殊判断。

​ 对于上下半凸包的点序列，讲其中一个视为点序列，另一个视为线段序列。判断点序列是否一直在线段序列的上方（或下方）。如果不是就说明有交。这个判断需要做两次，分别把上下半凸包视为点序列。

3. 伪代码

※ Map Overlay 的伪代码请参考 MapOverlay & Boolean Operations 实现讲解（PS/Photoshop布尔运算底层算法）

3.1 Half-plane Intersection

Algorithm INTERSECTHALFPLANES(H)
算法 INTERSECTHALFPLANES(H)
Input. A set H of n half-planes in the plane.
输入：由平面上n 张半平面组成的一个集合H
Output. The convex polygonal region C := ∩ h∈H h.
输出：凸多边形区域 C := ∩ h∈Hh
1. if card(H) = 1
1. if (card(H) == 1)
    2. then C <- the unique half-plane h ∈ H
    2. then C <- H 中唯一的那张半平面h
    3. else Split H into sets H1 and H2 of size ceilling(n/2) and floor(n/2).
    3. else 将H 分成两个子集H1 和H2，大小分别为ceilling(n/2)和floor(n/2)
        4. C1 <- INTERSECTHALFPLANES(H1)
        4. C1 <- INTERSECTHALFPLANES(H1)
        5. C2 <- INTERSECTHALFPLANES(H2)
        5. C2 <- INTERSECTHALFPLANES(H2)
        6. C <- INTERSECTCONVEXREGIONS(C1,C2)
        6. C <- INTERSECTCONVEXREGIONS(C1,C2)

3.2 Linear Programming

※ 有界Linear Programming 算法中，数学浓度最高部分为“1. 令v0 为C0 的角点”，这个角点判断还需结合实际生产情况来决定

// 有界Linear Programming
Algorithm 2DRANDOMIZEDBOUNDEDLP(H, →c, m1, m2)
算法 2DRANDOMIZEDBOUNDEDLP(H, →c, m1, m2)
Input. A linear program (H ∪ {m1,m2}, →c), where H is a set of n half-planes, c ∈ R2, and m1, m2 bound the solution.
输入：一个线性规划问题(H∪{m1, m2}, →c) (* 其中H 为由n 张半平面组成的一个集合，→c ∈ R2，m1 和m2 为解设定了边界 *)
Output. If (H ∪ {m1,m2}, →c) is infeasible, then this fact is reported. Otherwise, the lexicographically smallest point p that maximizes f→c(p) is reported.
输出：若(H∪{m1, m2}, →c)是不可行的，则报告这一情况否则，报告出使f→c(p)达到最大的（依字典序的）最小点
1. Let v0 be the corner of C0.
2. 令v0 为C0 的角点
3. Compute a random permutation h1, . . . ,hn of the half-planes by calling RANDOMPERMUTATION(H[1· · ·n]).
4. 调用RANDOMPERMUTATION(H[1…n])，生成这些半平面的一个随机排列：h1, h2, …, hn
5. for i <- 1 to n
6. for i <- 1 to n
   4. do if vi−1 ∈ hi
   4. do if vi−1 ∈ hi
      5. then vi <- vi−1
      6. then vi <- vi−1
      7. else vi <- the point p on li that maximizes fc(p), subject to the constraints in Hi−1.
      8. else vi <- 点p (* p来自li 上，它满足Hi-1 中的所有约束条件，而且使f→c (p)达到最大 *)
         7. if p does not exist
         7. if (点p 不存在)
            8. then Report that the linear program is infeasible and quit.
            8. then 报告“该线性规划问题不可行”，然后退出
7. return vn
8. return vn

※ 无界Linear Programming 算法中，数学浓度最高部分为“1. 判断是否存在某个方向矢量→d，满足→d·→c > 0，并且对所有的h ∈ H 都有→d·→η (h) ≥ 0”，教材上有关于这个矢量d的判断方法，但是笔者数学功力实在不够，没法理解实现哦

// 无界Linear Programming
Algorithm 2DRANDOMIZEDLP(H, →c)
算法 2DRANDOMIZEDLP(H, →c)
Input. A linear program (H, →c), where H is a set of n half-planes and→c ∈ R2.
输入：线性规划问题(H, →c)，其中H 为由n 张半平面组成的一个集合，→c ∈ R2。
Output. If (H, →c) is unbounded, a ray is reported. If it is infeasible, then two or three certificate half-planes are reported. Otherwise, the lexicographically smallest point p that maximizes fc(p) is reported.
输出：若(H, →c)是无界的，则返回一条射线若不可行，则返回两到三张作为凭证的半平面否则，在使函数f→c达到最大的那些点中，返回字典序最小者。
1. Determine whether there is a direction vector →d such that →d · →c > 0 and →d · η(h) >= 0 for all h ∈ H.
1. 判断是否存在某个方向矢量→d，满足→d·→c > 0，并且对所有的h ∈ H 都有→d·→η (h) ≥ 0
2. if →d exists
2. if (这样的 →d存在)
    3. then compute H' and determine whether H' is feasible.
    3. then 计算出H'，并判断H'是否可行
        4. if H' is feasible
        4. if (H'是可行的)
            5. then Report a ray proving that (H, →c) is unbounded and quit.
            5. then 报告一条可以证明(H, →c)无界的射线，然后退出算法
            6. else Report that (H, →c) is infeasible and quit.
            6. else 报告“(H, →c)是不可行的”，然后退出算法
7. Let h1,h2 ∈ H be certificates proving that (H, →c) is bounded and has a unique lexicographically smallest solution.
7. 令h1, h2 ∈ H 为所谓的“凭证”半平面 (* 它们确保了(H, →c)的有界性，同时说明按照字典序，该问题存在唯一的最小解 *)
8. Let v2 be the intersection of l1 and l2.
8. 令v2 为l1 和l2 的交点
9. Let h3,h4, . . . ,hn be a random permutation of the remaining half-planes in H.
9. 设h3, h4, …, hn 为H 中其余半平面的一个随机排列
10. for i <- 3 to n
10. for i <- 3 to n
    11. do if vi−1 ∈ hi
    11. do if vi−1 ∈ hi
        12. then vi <- vi−1
        12. then vi <- vi−1
        13. else vi <- the point p on li that maximizes fc(p), subject to the constraints in Hi−1.
        13. else vi <- p (* p来自li 上，它满足Hi-1 中所有约束条件，并使函数f→c达到最大 *)
            14. if p does not exist
            14. if (p 不存在)
                15. then Let hj,hk (with j,k < i) be the certificates (possibly hj = hk) with hj ∩ hk ∩ li = ∅.
                15. then 令hj 和hk 为满足hj ∩ hk ∩ li = ∅的两张凭证半平面 (* j, k < i，但是有可能hj = hk *)
                16. Report that the linear program is infeasible, with hi,hj,hk as certificates, and quit.
                16. 报告“该线性规划问题是不可行的”提供凭证半平面hi、hj 和hk 退出算法
17. return vn
17. return vn

4. 可视化结果示例

这里给到题目网页上的一个实例的可视化结果，左边的结果是线段在对偶平面求得的半平面相交区域，右边的结果是可视化解集中的其中一个解（一条满足题意的直线）

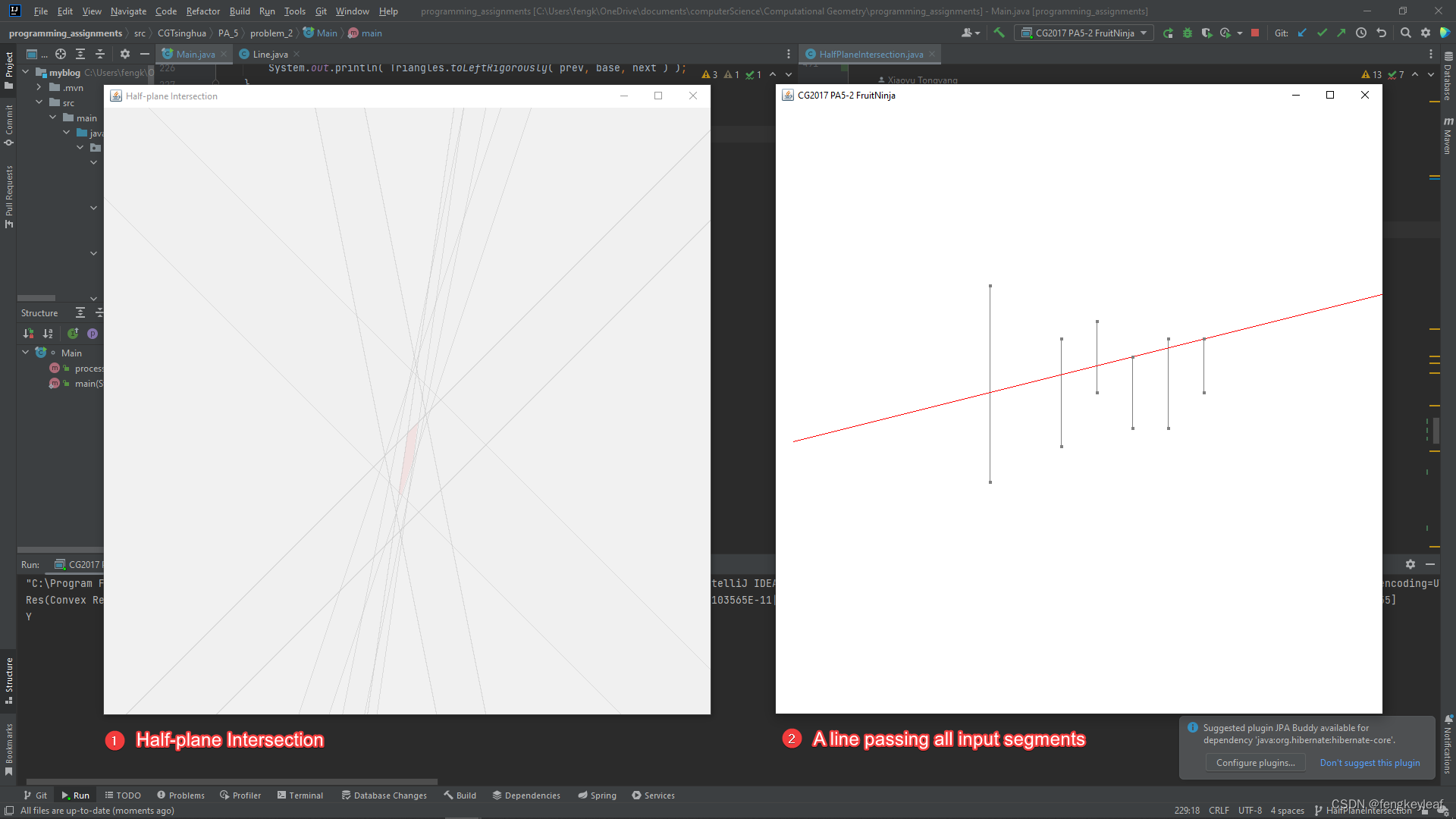
5. 项目代码

个人作业项目代码：Algorithm

1.1.10 MapOverlay & Boolean Operations

Description	Entry method\File
Computing the overlay of two subdivisions	Face compute( Face s1, Face s2 )
Compute the intersection of two subdivisions, P1 ∩ P2.	List<Face> intersection( Face s1, Face s2 )
Compute the union of two subdivisions, P1 ∪ P2,	List<Face> union( Face s1, Face s2 )
Compute the difference of two subdivisions, P1 \ P2.	List<Face> difference( Face s1, Face s2 )

1.1.11 Half-plane Intersection

Description	Entry method\File
Compute half-plane intersection.	void intersect( List<HalfPlane> H )
Get current result type.	Type getResultType()
Program ( including visualization )	CG2017 PA5-2 FruitNinja

1.1.12 Duality

Description	Entry method\File
Transform this point in the primary plane into the dual plane, point to line.	Line toDuality()
Transform this point in the dual plane into the primary plane, point to line.	Line fromDuality()
Transform this line in the primary plane into the dual plane, line to point.	Vector toDuality()

6. 拓展（Follow-ups）

• 使用 Linear Programming 对本题进行求解，以达到最优时间复杂度O( n )；
• 是否有方法可以不使用 Bounding Box 来进行 Half-plane 有限化，也能正确求得Half-plane Intersection；

7. 参考资料

1. Computational Geometry: Algorithms and Applications
2. 计算几何 ⎯⎯ 算法与应用, 邓俊辉译，清华大学出版社
3. 计算几何 | Computational Geometry

8. 免责声明

※ 本文之中如有错误和不准确的地方，欢迎大家指正哒~
※ 此项目仅用于学习交流，请不要用于任何形式的商用用途，谢谢呢；

---

---

1. 计算几何 ⎯⎯ 算法与应用, 邓俊辉译，清华大学出版社 ↩︎ ↩︎ ↩︎