Voronoi图（一）：塞尔达背后的计算几何

fengkeyleaf

已于 2023-05-10 22:34:22 修改

阅读量1.4k

点赞数 8

分类专栏：计算几何算法文章标签：算法计算几何 Voronoi图

于 2022-03-22 12:15:33 首次发布

本文链接：https://blog.csdn.net/fengkeyleaf/article/details/123657278

版权

算法同时被 2 个专栏收录

74 篇文章

订阅专栏

计算几何

34 篇文章

订阅专栏

Voronoi图（一）：塞尔达背后的计算几何

1. 林克的难题
2. 巧用Voronoi图
3. 个人项目招募
4. 参考资料
5. 免责声明

1. 林克的难题

玩过塞尔达传说：荒野之息的朋友，应该都会赞叹海拉鲁风景的美丽。我们的林克时不时一人独自在战后废墟中探索一座座神庙，有时武器库告急，也会偶尔探望一下亲爱的人马们。现在林克一个人游荡在海拉鲁大地上，遇到了一个难题：他突然想回到河畔驿站修整一下，恢复心心，但是他究竟需要传送哪个传送塔，才能离驿站最近呢？下图给出了河畔驿站的位置，以及三个比较近的传送塔：平原之塔，双子山之塔和初始之塔：

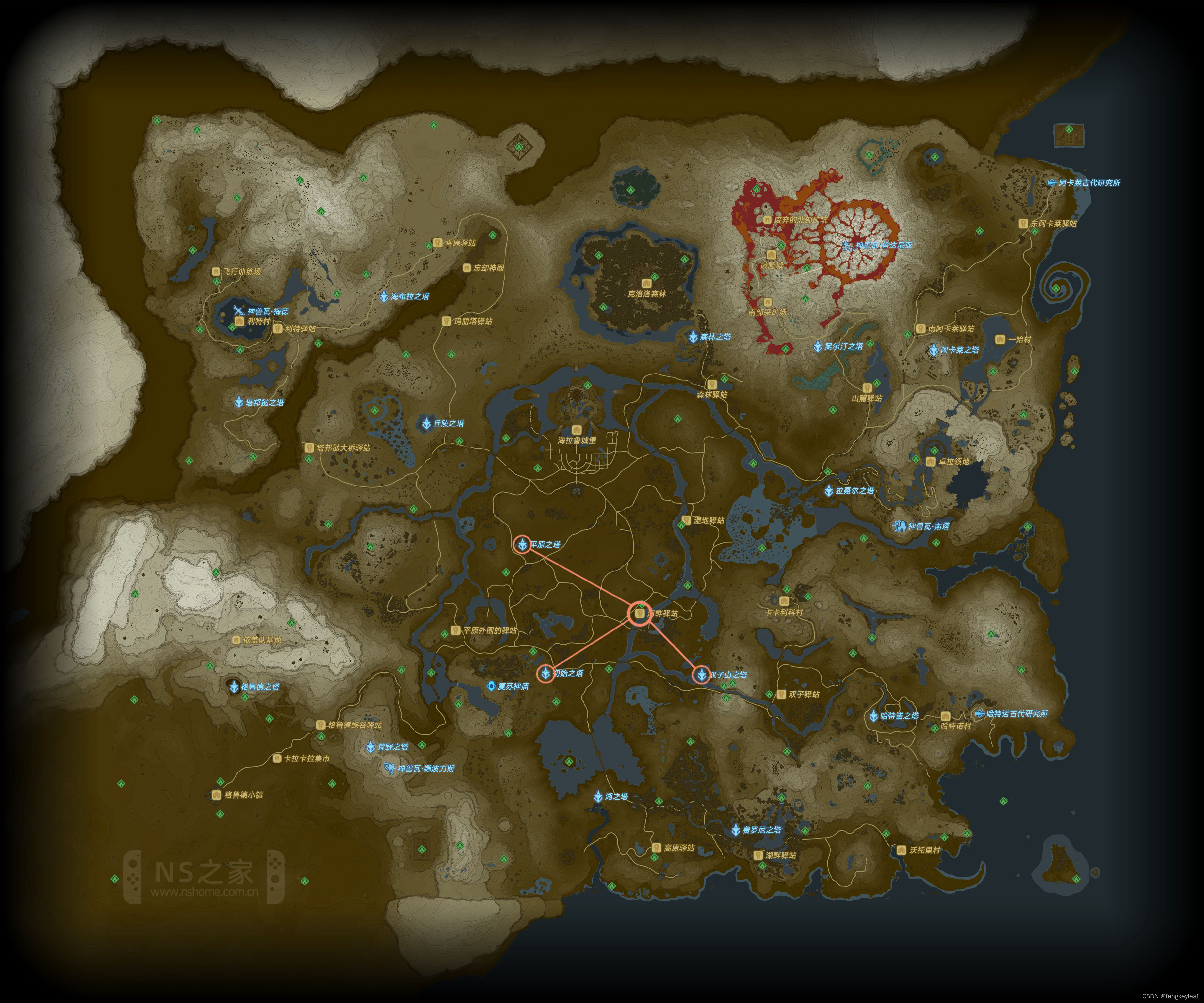
在这里插入图片描述

为了简化问题，这里我们限制传送点只能是传送塔，神庙等的传送点无效；“离驿站最近”是指传送塔距离驿站的直线距离，当然实际赶路可能不能走直线，不过可以用风弹逃课啦哒~

那么，林克究竟应该选择传送到哪个传送塔呢？我们能用什么方法帮助林克解决这个难题呢？其实这个问题可以转换成计算几何中的Voronoi Diagrams（Voronoi图）问题，只要使用传送塔作为输入点，并计算相应的Voronoi图，我们就能得到想要的答案！

2. 巧用Voronoi图

针对这个问题，可能有童鞋会说直接比较驿站到传送点的直线距离，距离最短就是我们想要的结果。通过上面的图例，我们一眼就能知道双子山之塔最近。但是这个方法的效率如何呢？假设我们有n个传送点，那计算所有距离我们需要O(n)的时间，接近线性时间，似乎好像还挺不错的嘛。注意这里是查询一次的效率，假设我们查询了k次，那么总的时间为：O( n ) * k；如果k = n，那么总的时间为：O( n ^ 2 )，查询效率将会大大地降低。

那有没有更加高效的查询方法呢？或者说，我们是否能先建立一个高效的查询数据结构，让我们每次查询效率更高，即使查询次数够多，也能保证查询的整体效率。其实这就是Offline Algorithm 和 Online Algorithm 的区别，这点我们在线段树（二）：RMQ 也提到过呢。

这里我们会把传送塔看成输入点，对点集计算对应的Voronoi图，然后结合点定位算法，就能高效进行空间点的查询。接下来，我们就来看看如何巧用Voronoi图的性质来解决林克的难题吧。

首先，我们用传送塔作为输入点，计算相应的Voronoi图：
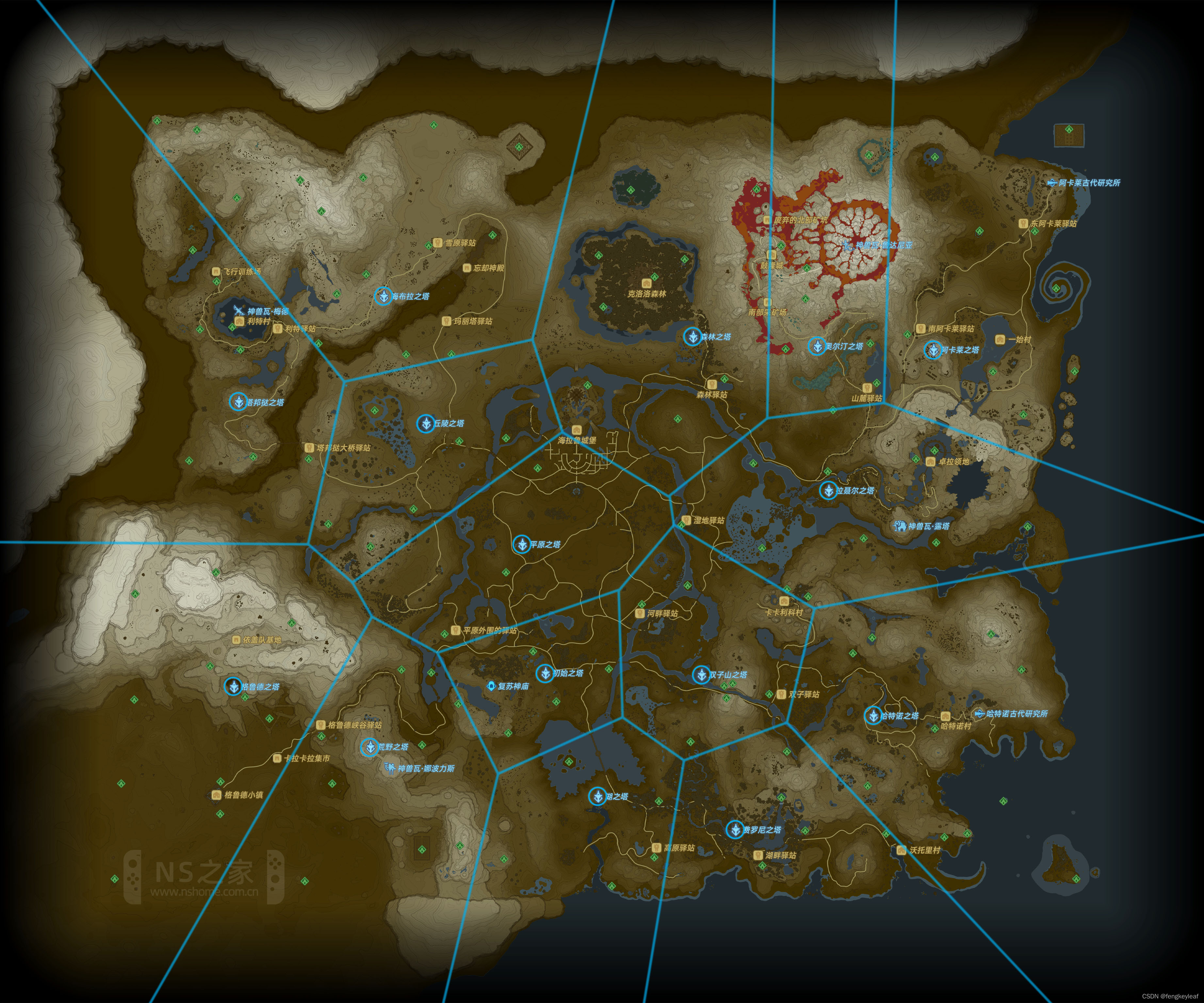
在这里插入图片描述
大家可以看到，被蓝线围成的一块块区域，就是Voronoi Cell，每个Cell都会包含一个输入点（传送点），我们也称输入点为SIte。在得到Voronoi图之后，我们也得到了一个非常有用的性质：

每个Cell里面的任一点，到这个Cell包含的SIte的直线距离是最短的。

运用这个性质，我们来看看之前三个候选的传送塔所在的Cell，以及湖畔驿站所在的Cell：
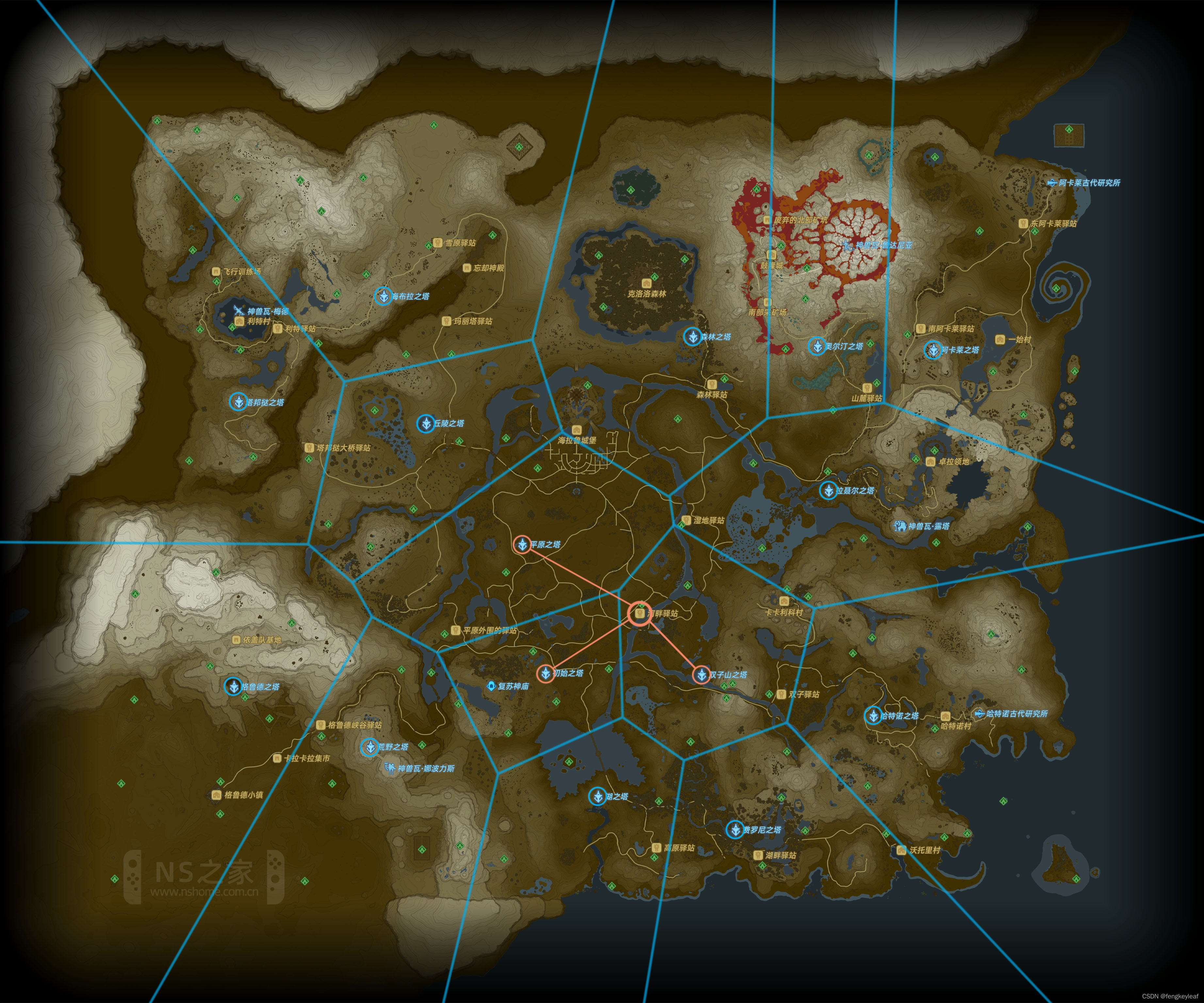
在这里插入图片描述
我们可以看到，只有双子山之塔和河畔驿站处在同一个Cell里面，平原之塔和初始之塔分别在两个不同的Cell里面，所以我们应该让林克传送到双子山之塔，距离河畔驿站最近：

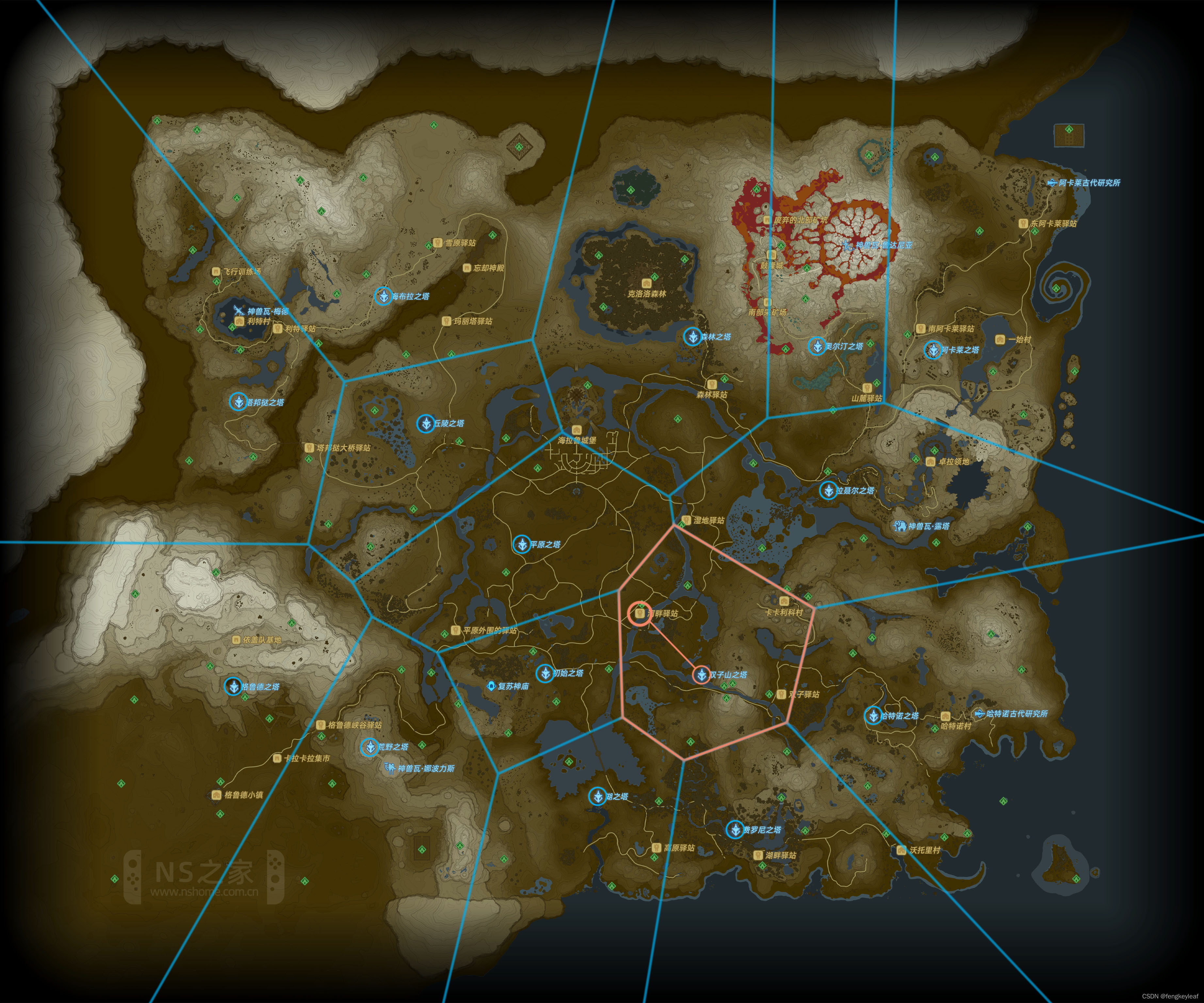
有了Voronoi图，我们无论进行多少次查询，每次查询的时间都是：O( logn )。建立Voronoi图和与之对应的梯形图（Trapezoidal Map）需要O( nlogn )，假如一共查询了k（k = n）次，整体的时间复杂度为：

2 * O( n logn ) + k * O( logn ) = 2 * O( n logn ) + n * O( logn ) = O( n logn )；

现在时间复杂度比之前的O( n ^ 2 )好了不少，从这里大家也能感受到Voronoi图对空间查询效率的提升。好啦，我们帮助林克解决了难度，他也能继续在海拉鲁的冒险，最后拯救塞尔达公主！那接下来我们就来看看Voronoi图一些重要的性质，以及讲解搭建Voronoi图的算法。

3. 个人项目招募

号外哒，号外哒~ 现在想做一个以Voronoi图算法的塞尔达野炊网页项目哒。想法就是用上面提到的算法去做一个演示网站：比如用户随意输入一个目标点，网页能呈现Voronoi图和相应最近的传送点（包括神庙，神兽等等）。具体的效果交互还没有想好哒，正在构思中，也在倒腾个人网站的搭建~ 如果你对该项目有兴趣，长期招募下面的小伙伴哒：