原帖地址:http://blog.csdn.net/maverick1990/article/details/12564973
牛顿方法
本次课程大纲:
1、 牛顿方法:对Logistic模型进行拟合
2、 指数分布族
3、 广义线性模型(GLM):联系Logistic回归和最小二乘模型
复习:
Logistic回归:分类算法
假设给定x以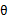
求对数似然性:
对其求偏导数,应用梯度上升方法,求得:
本次课程介绍的牛顿方法是一种比梯度上升快很多的方法,用于拟合Logistic回归
1、 牛顿方法
假设有函数

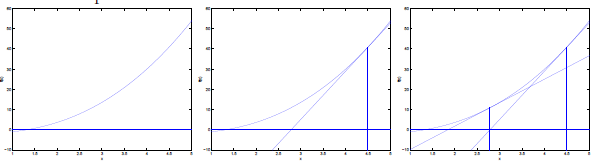
步骤:
1) 给出一个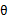
2) 对
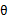

3) 重复步骤2
因为该点的导数值即为切线斜率,而斜率=该点y轴的值/该点x轴的变化值,所以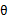
*使用这个方法需要f满足一定条件,适用于Logistic回归和广义线性模型
* 一般初始化为0
应用于Logistic回归:
求对数似然的最大值,即求
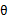
牛顿方法的收敛速度:二次收敛
每次迭代使解的有效数字的数目加倍:假设当前误差是0.01,一次迭代后,误差为0.001,再一次迭代,误差为0.0000001。该性质当解距离最优质的足够近才会发现。
牛顿方法的一般化:
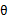
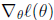
上述公式的意义就是,用一个一阶导数的向量乘以一个二阶导数矩阵的逆
优点:若特征数和样本数合理,牛顿方法的迭代次数比梯度上升要少得多
缺点:每次迭代都要重新计算Hessian矩阵,如果特征很多,则H矩阵计算代价很大
2、 指数分布族
回顾学过的两种算法:
对于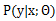
若y属于实数,满足高斯分布,得到基于最小二乘法的线性回归;
若y取{0,1},满足伯努利分布,得到Logistic回归。
问题:如Logistic回归中,为何选择sigmoid函数?sigmoid函数是最自然的默认选择。
接下来,会以这两个算法为例,说明它们都是广义线性模型的特例。
考虑上述两个分布,伯努利分布和高斯分布:
1) 伯努利分布
设有一组只能取0或1的数据,用伯努利随机变量对其建模:
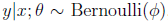

2) 高斯分布

上述这些分布都是一类分布的特例,这类分布称为指数分布族。
指数分布族的定义:
若一类概率分布可以写成如下形式,那么它就属于指数分布族:
η - 自然参数,通常是一个实数
T(y) – 充分统计量,通常,T(y)=y,实际上是一个概率分布的充分统计量(统计学知识)
对于给定的a,b,T三个函数,上式定义了一个以η为参数的概率分布集合,即改变η可以得到不同的概率分布。
证明伯努利分布是指数分布族:
可知:
由上式可见,η=log(φ/(1-φ)),可解出:φ=1/(1+exp(-η)),发现得到logistic函数(之后讨论其原因),则:
证明高斯分布是指数分布族:

这种情况下高斯密度函数为:
可得:
*指数分布族包括:
高斯分布(正态分布),多元正态分布;
伯努利分布(01问题建模),多项式分布(对k个结果的事件建模);
泊松分布(对计数过程建模);
伽马分布,指数分布(对实数的间隔问题建模);
β分布,Dirichlet分布(对小数建模);
Wishart分布(协方差矩阵的分布)…
3、 广义线性模型GLM
选定了一个指数分布族后,怎样来推导出一个GLM呢?
假设:
(1)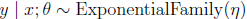
例:若要统计网站点击量y,用泊松分布建模
(2) 给定x,目标是求出以x为条件的T(y)的期望E[T(y)|x],即让学习算法输出h(x) = E[T(y)|x]
(3)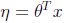
推导伯努利分布的GLM:
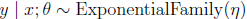
对给定的x,θ,学习算法进行一次预测的输出:
得到logistic回归算法。
正则响应函数:g(η) = E[y;η],将自然参数η和y的期望联系起来
正则关联函数:g-1
推导多项式分布的GLM:
多项式分布是在k个可能取值上的分布,即y∈{1,…,k},如将收到的邮件分成k类,诊断某病人为k种病中的一种等问题。
(1)将多项式分布写成指数分布族的形式:
设多项式分布的参数:
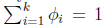
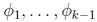
多项式分布是少数几个T(y)!=y的分布,T(1)~T(k)都定义成一个k-1维的列向量,表示为:
这样定义T(y)是为了将多项式分布写成指数分布族形式。
*定义符号:指示函数,1{.}
1{True} = 1, 1{False} = 0,即大括号内命题为真,值为1,;否则为0。
例:1{2=3} = 0, 1{1+1=2} = 1
用T(y)i表示T(y)的第i个元素,则T(y)i = 1{y=i}
根据参数φ的意义(φi表示第i个取值的概率分布),可推出:
可得:
证明多项式分布式指数分布族。
再用η表示φ:
(2)根据上述假设(3)中自然参数和输入x的线性关系,可求得:
(3)根据上述假设(2)中的输出h(x) = E[T(y)|x],可求得:
称这种回归算法为softmax回归,是logistic回归的推广。
Softmax回归的训练方法和logistic相似,通过极大似然估计找到参数θ,其对数似然性为:
再通过梯度上升或牛顿方法找对数似然性的最大值,即可求出参数θ。








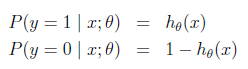

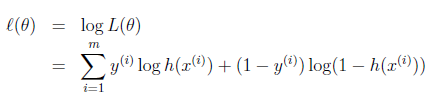
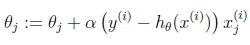
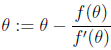
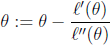
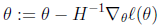
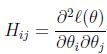
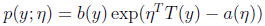
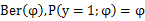
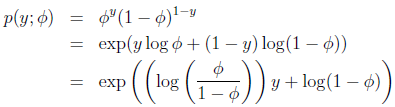
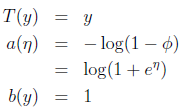
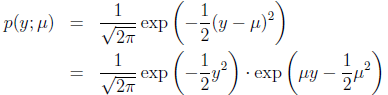
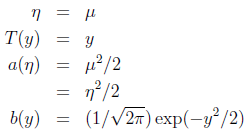
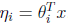
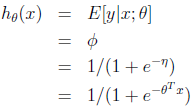
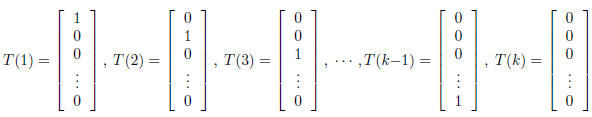
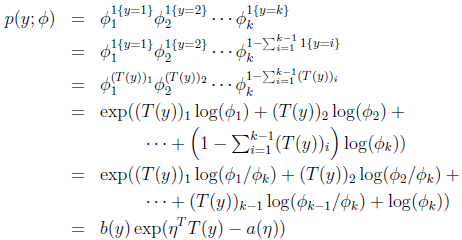
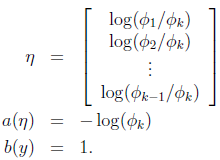
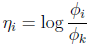
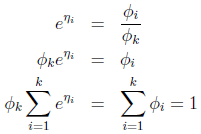
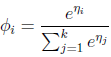
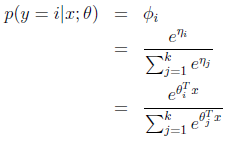

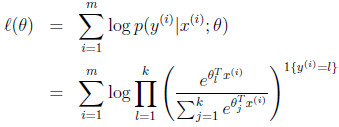














 1624
1624

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








