知乎链接
https://www.zhihu.com/question/36301367
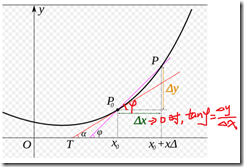
导数:
导数不仅仅表示该点切线的斜率,还反应了函数在该点的变化率。
偏导数:
偏导数仅仅是表示某点在x方向的导数和再y轴方向的导数。
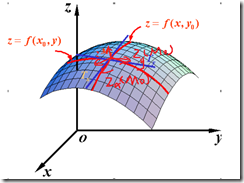
这反应了偏导数的局限性,仅仅是多元函数沿着坐标轴的变化率,但是如上图,在M0点处存在很多方向的偏导数(并不仅仅x和y方向)。这就引出了方向导数。
方向导数:
我们不仅仅要知道函数在坐标轴方向上的变化率(即偏导数)还需要设法求得函数在其他方向上的变化率。而方向导数就是函数在其他特定方向上的变化率。
方向导数的定义和导数定义类似,只不过是在多个维度上。例如在三维空间中:
设三元函数f在点P0(x0,y0,z0)的某邻域内有定义,l为从点P0出发的射线,P(x,y,z)为l上且含于邻域内的任一点,以ρ(rou)表示P和P0两点间的距离。若极限
lim( (f(P)-f(P0)) / ρ )= lim (△l f / ρ)(当ρ→0时)
存在,则称此极限为函数f在点P0沿方向l的方向导数
梯度:
由上面的方向导数可知,方向导数是在各个方向上都有,而且每个方向上的变化一般是不一样的,那到底沿哪个方向最大呢?沿哪个方向最小呢?为了研究方便,就有了梯度的定义。
下图是梯度的定义:
梯度是众多方向导数中最大的那个向量,这个方向就用梯度来表示(grad=ai+bj)这个向量来表示,其中a是函数在x方向上的偏导数,b是函数在y方向上的偏导数,梯度的模就是这个最大方向导数的值。








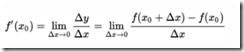















 839
839

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








