李沐深度学习预备知识——微积分

李沐深度学习预备知识——微积分

---

1、拟合模型的任务

• 优化：拟合训练数据
• 泛化：改进模型的泛化性能

2、导数、微分，偏导、梯度，链式法则

• 导数
  
  $D$是微分运算符，等同于d/dx

• 偏导
  
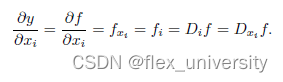
  $D_i$是微分运算符，对i求偏导

• 梯度
  
  多元函数视作是输入向量得到标量的函数，而对所有输入的元的梯度，可以简化写法如上。
  
  加入矩阵变换的微分，n*m矩阵，相当于多个方程求微分，故得到1xm的结果，每列为对应方程微分。
  上图最后一行，对于矩阵求偏导，实际上是对矩阵每个位置分别求偏导再放到原位上构成新的偏导矩阵。

• 链式法则
  对于多元复合函数，上述规则难以求解微分，需要使用链式法则。
  首先考虑单变量函数
  
  再考虑多元复合函数
  

3、自动微分工具（automatic differentiation）

pytorch自动微分：根据设计好的模型，系统会构建一个计算图（computational graph），来跟踪计算是哪些数据通过哪些操作组合起来产生输出。自动微分使系统能够随后反向传播梯度。这里，反向传播（backpropagate）意味着跟踪整个计算图，填充关于每个参数的偏导数。

---

示例1，对列向量函数$y=2x^{T}x$关于列向量求导

import torch
x = torch.arange(4.0)
x

计算y关于x的梯度之前，需要一个地方来存储梯度。重要的是，我们不会在每次对一个参数求导时都分配新的内存。因为我们经常会成千上万次地更新相同的参数，每次都分配新的内存可能很快就会将内存耗尽。这是自动微分的计算图的作用。

x.requires_grad_(True) # 等价于x=torch.arange(4.0,requires_grad=True)
x.grad # grad为一个属性，访问张量对象的梯度。默认值是None
y = 2 * torch.dot(x, x)
y.backward()
x.grad #得到梯度

下面换一个简单的多变量相加的函数试试

# 在默认情况下，PyTorch会累积梯度，我们需要清除之前的值
x.grad.zero_()
y = x.sum() # x1+x2+x3
y.backward()
x.grad

为什么需要清零梯度
batch：在深度学习中，batch（批次）是指一次性输入到神经网络的一组样本。通常情况下，训练过程中的数据集会被分成多个批次进行处理。通过将数据分成批次，可以有效地处理大规模数据集，并且在梯度下降过程中能够更好地进行参数更新。在每个批次中，样本会被送入网络进行前向传播和反向传播，然后使用批次内的样本计算出平均损失值，并利用该损失值来更新网络的参数。批次大小（即每个批次中包含的样本数量）是一个超参数，可以根据数据集的大小和计算资源的限制进行调整。较大的批次大小可以提高计算效率，但可能导致模型的泛化能力下降；较小的批次大小可以提高模型的泛化能力，但可能会增加计算开销。

---

示例2，非标量变量的反向传播：
待更

---

示例3，分离计算

---

示例4，python控制流的梯度计算