激光光栅 学习

光纤光栅

光纤光栅是一种通过一定方法使光纤纤芯的折射率发生轴向周期性调制而形成的衍射光栅，是一种无源滤波器件。由于光栅光纤具有体积小、熔接损耗小、全兼容于光纤、能埋入智能材料等优点，并且其谐振波长对温度、应变、折射率、浓度等外界环境的变化比较敏感，因此在制作光纤激光器、光纤通信和传感领域得到了广泛的应用

光纤光栅主要的制作方法是利用光纤材料的光敏性，通过紫外光曝光的方法将入射光相干场图样写入纤芯，在纤芯内产生沿纤芯轴向的折射率周期性变化，从而形成永久性空间的相位光栅，其作用实质上是在纤芯内形成一个窄带的（透射或反射）滤波器或反射镜。当一束宽光谱光经过光纤光栅时，满足光纤光栅布拉格条件的波长将产生反射，其余的波长透过光纤光栅继续传输。

目前，大部分的衍射光栅产品均由母版复制而成，母版制备工艺主要有精密机械刻划、可离子束增强的全息制版，另外也有一些诸如半导体光刻等新的科技手段。

　　光栅方程

　　一个典型的衍射光栅包括基底（通常为光学材料），其表面通过加工形成的大量平行凹槽，以及表面镀有的铝膜等反射膜构成。凹槽的质量和间距是光栅参数的关键指标。若假定光栅表面与其刻划方向正交的部分是锯齿型，可以导出光栅基本方程。

　　波长为l的光束A和B，与光栅法线(Grating Normal)成角度I入射到相邻凹槽。衍射光线A’和B’与光栅法线成角度D。二者光程差可表示为：

　　a sin I + a sin D

　　当光程差是波长l的任意整数倍时，光束A’和B’的叠加会产生相长干涉：

　　a(sin I + sin D) = mλ

　　其中m为整数，即衍射级数。

　　这是光栅基本方程。若D与I在光栅法线的两边，m取负值。

　　以上为假定只有两凹槽的简化情况，而综合考虑其他所有凹槽，光栅衍射基本方程也不会改变，不过会增大衍射强度相对衍射角D的灵敏度。

　　图1： 锯齿型光栅

　　实际光栅方程

　　平行的单色光光束照射到光栅上，会产生不同级次的衍射，如图2所示。在“光栅衍射级次”章节中将详述。

　　平行的多色光光束照射到光栅上，会产生色散，以使不同波长均满足光栅方程，如图3所示。

　　图2.平行单色光满足的光栅方程

　　图3.经光栅衍射的多色光。图中仅显示负的衍射级次。

　　大部分单色仪中，入射狭缝和准直镜确定了光栅入射光的方向，聚焦镜和出射狭缝确定了出射光的方向。只有符合光栅方程的波长可以透过出射狭缝，其余的光在单色仪内被散射及吸收。虽然旋转光栅会改变入射角I和衍射角D，但它们的差值始终保持恒定，这取决于单色仪的几何构造。

　　单色仪更适用以下形式的光栅方程：

　　mλ = 2 x a x cos φ x sin θ

　　其中：φ =入射光衍射光夹角的一半

　　θ =光栅相对零级位置的角度

　　这些参数与入射角I和衍射角D的关系可表为

　　I = θ + φ，D = θ – φ

　　光栅衍射级次

　　衍射级次“m”的正负可由任一形式的光栅方程决定。单色仪中，入射角I和衍射角D取决于光栅的旋转。本文将所有在光栅法线逆时针方向的角度设定为正，顺时针方向的设定为负，如图4所示。半角φ始终为正。

　　如果D和I大小相同方向相反，光栅角度和级次均为0，光束全部被反射。当光栅角度为正时级次为正（m=1），反之级次为负（m=-1）。

　　当|m|>1时，光栅方程在高级次下亦成立，如m = ±2时λ2=λ1/2，m = ±3时λ3 = λ1/3等。λ2 和λ3即属于二级和三级对应的波长，定义由图3给出。

　　实际应用通常只需要一级衍射，其他高级次下的波长需要被滤除。入射光谱范围和探测器的灵敏度决定了是否需要使用选通或截止滤光片。

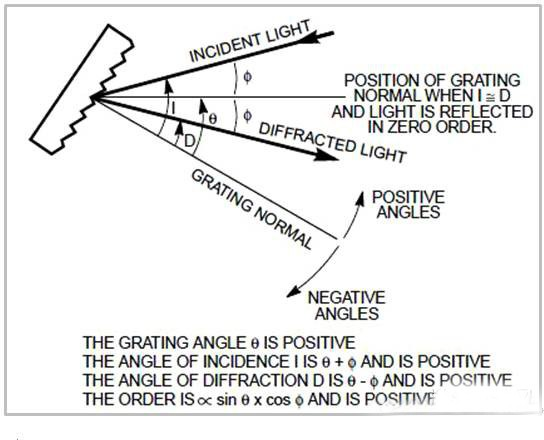
　　图4.对入射角I、衍射角D和光栅角q的正负的定义。