【数学】数列极限（宇哥笔记）

定义

数列

按照一定顺序排列的“有开头无结尾”的数叫（无穷）数列。

$$\begin{gathered} x_1,x_2,\dots ,x_n,\dots \\ 首项通项 \end{gathered}$$
数列极限
∀ ϵ &gt; 0 , ∃ N &gt; 0 , n &gt; N 时 ， ∣ x n − A ∣ &lt; ϵ &ThickSpace; ⟺ &ThickSpace; lim ⁡ n → ∞ x n = A &ThickSpace; ⟺ &ThickSpace; { x n } 收 敛 于 A [ 注 ] 1. n 为 正 整 数 ； 2. lim ⁡ n → ∞ x n + 1 = A 也 常 用 \forall\epsilon&gt;0,\exists N&gt;0,n&gt;N时，\mid x_n-A\mid&lt;\epsilon\iff\lim_{n\to\infty}x_n=A\iff \lbrace x_n\rbrace收敛于A\\ \color{grey}[注]1.n为正整数；2.\lim_{n\to\infty}x_{n+1}=A也常用 ∀ϵ>0,∃N>0,n>N时，∣xn​−A∣<ϵ⟺n→∞lim​xn​=A⟺{xn​}收敛于A[注]1.n为正整数；2.n→∞lim​xn+1​=A也常用

性质

$$\begin{gathered} 1.唯一性\underset{n\to \infty }{\lim }{x}_n=A⟹A唯一 \\ 2.有界性\underset{n\to \infty }{\lim }{x}_n=A⟹\mid x_n\mid \le M \\ 3.保号性若x_n\ge 0,\underset{n\to \infty }{\lim }{x}_n=A,则A\ge 0 \end{gathered}$$
考法

1.直接计算法
2.单调有界法则
3.定义法
4.夹逼准则
5.定积分定义

直接计算法

$$\begin{gathered} 两个公式：1.S_n=a+aq+a{q}^2+\dots +a{q}^{n-1}=\frac{a(1-q^n)}{1-q}(q̸=1) \\ 2.\mid q\mid <1,\underset{n\to \infty }{\lim }{S}_n=\underset{n\to \infty }{\lim }\frac{a(1-q^n)}{1-q}=\frac{a}{1-q} \end{gathered}$$
$$[例1]设a_0=0,a_1=1,a_n+a_{n-1}=2a_{n+1},求\underset{n\to \infty }{\lim }{a}_n$$
$$\begin{gathered} [分析]a_{n+1}=\frac{a_n+a_{n-1}}{2}⟹ \\ 做差a_{n+1}-a_n=\frac{a_n+a_{n-1}}{2}-a_n=\frac{a_{n-1}-a_n}{2}=-\frac{1}{2}(a_n-a_{n-1}) \\ =(-\frac{1}{2}{)}^n(a_1-a_0) \\ 即a_{n+1}-a_n=(-\frac{1}{2}{)}^n\therefore a_n=(a_n-a_{n-1})+(a_{n-1}-a_{n-2})+(a_{n-2}-a_{n-3})+\dots +(a_1-a_0)+a_0 \\ =(-\frac{1}{2}{)}^{n-1}+（-\frac{1}{2}{)}^{n-2}+\dots +1=\frac{1\cdot [1-(-\frac{1}{2}{)}^n]}{1-(-\frac{1}{2})} \\ 故\underset{n\to \infty }{\lim }{a}_n=\underset{n\to \infty }{\lim }\frac{1-(-\frac{1}{2}{)}^n}{1-(-\frac{1}{2})}=\frac{2}{3} \end{gathered}$$
$$[变体一]设x_1=1,x_2=2,x_{n+2}=\sqrt{x_{n+1}\cdot x_n},求\underset{n\to \infty }{\lim }{x}_n$$
$$\begin{gathered} [分析]取对数，\ln x_{n+2}=\ln \sqrt{x_{n+1}\cdot x_n}=\frac{1}{2}\ln x_{n+1}+\frac{1}{2}\ln x_n \\ 令y_n=\ln x_n⟹y_{n+2}=\frac{1}{2}(y_{n+1}+y_n) \\ 故y_{n+2}-y_{n+1}=\frac{1}{2}(y_{n+1}+y_n)-y_{n+1}=-\frac{1}{2}(y_{n+1}-y_n)=(-\frac{1}{2}{)}^n(y_2-y_1)=\ln 2(-\frac{1}{2}{)}^n \\ {y}_n=(y_n-y_{n-1})+(y_{n-1}-y_{n-2})+\dots +(y_2-y_1)+y_1=\ln 2[(-\frac{1}{2}{)}^{n-2}+(-\frac{1}{2}{)}^{n-3}+\dots +1] \\ =\ln 2\cdot \frac{1\cdot [1-(-\frac{1}{2}{)}^{n-1}]}{1-(-\frac{1}{2})}⟹\underset{n\to \infty }{\lim }{y}_n=\ln 2\cdot \frac{2}{3}=\underset{n\to \infty }{\lim }\ln x_n⟹\underset{n\to \infty }{\lim }{x}_n=e^{\frac{2}{3}\ln 2}=2^{\frac{2}{3}} \end{gathered}$$
$$\begin{gathered} [变体二]设a_1=1,a_2=2,a_{n+2}=\frac{2a_n{a}_{n+1}}{a_n+a_{n+1}},n=1,2,\dots \\ (Ⅰ)求b_n=\frac{1}{a_{n+1}}-\frac{1}{a_n}的表达式并求\sum _{k=1}^n{b}_k \\ (Ⅱ)求\underset{n\to \infty }{\lim }{a}_n \end{gathered}$$
$$\begin{gathered} [分析](Ⅰ)求倒数\frac{1}{a_{n+2}}=\frac{a_n+a_{n+1}}{2a_n{a}_{n+1}}=\frac{1}{2}(\frac{1}{a_n}+\frac{1}{a_{n+1}}) \\ \therefore \frac{1}{a_{n+2}}-\frac{1}{a_{n+1}}=\frac{1}{2}(\frac{1}{a_n}+\frac{1}{a_{n+1}})-\frac{1}{a_{n+1}} \\ =(-\frac{1}{2})(\frac{1}{a_{n+1}}-\frac{1}{a_n}) \\ =(-\frac{1}{2}{)}^n(\frac{1}{a_2}-\frac{1}{a_1})=(-\frac{1}{2}{)}^{n+1} \\ {b}_n=\frac{1}{a_{n+1}}-\frac{1}{a_n}=(-\frac{1}{2}{)}^n \\ \sum _{k=1}^n{b}_k=(-\frac{1}{2}{)}^1+(-\frac{1}{2}{)}^2+\dots +(-\frac{1}{2}{)}^n=\frac{(-\frac{1}{2})[1-(-\frac{1}{2}{)}^n]}{1-(-\frac{1}{2})} \\ (Ⅱ)\sum _{k=1}^n{b}_k=b_1+b_2+\dots +b_k \\ =(\frac{1}{a_2}-\frac{1}{a_1})+(\frac{1}{a_3}-\frac{1}{a_2})+\dots +(\frac{1}{a_{n+1}}-\frac{1}{a_n}) \\ =\frac{1}{a_{n+1}}-\frac{1}{a_1}⟹a_{n+1}=\frac{1}{{\sum }_{k=1}^n{b}_k+1} \\ 故\underset{n\to \infty }{\lim }{a}_{n+1}=\frac{3}{2} \end{gathered}$$

单调有界准则

定 义 { { x n } ↑ 且 有 上 界 { x n } ↓ 且 有 下 界 &ThickSpace; ⟹ &ThickSpace; lim ⁡ n → ∞ x n 存 在 要 点 { 作 差 x n + 1 − x n 作 商 x n + 1 x n 数 学 归 纳 法 、 不 等 式 、 有 提 示 x n + 1 = f ( x ) , 证 明 lim ⁡ n → ∞ 存 在 并 求 之 \left.定义\begin{cases}\lbrace x_n\rbrace\uparrow且有上界\\\lbrace x_n\rbrace\downarrow且有下界 \end{cases}\right.\implies\lim_{n\to\infty}x_n存在\qquad\quad\\ \left.要点\begin{cases}作差x_{n+1}-x_n\\作商\frac{x_{n+1}}{x_n}\end{cases}\right.数学归纳法、不等式、有提示\\ x_{n+1}=f(x),证明\lim_{n\to\infty}存在并求之\qquad\qquad\qquad 定义{{xn​}↑且有上界{xn​}↓且有下界​⟹n→∞lim​xn​存在要点{作差xn+1​−xn​作商xn​xn+1​​​数学归纳法、不等式、有提示xn+1​=f(x),证明n→∞lim​存在并求之
[ 例 1 ] { a n } ↓ , { b n } ↑ , lim ⁡ n → ∞ ( a n − b n ) = 0 , 证 明 lim ⁡ n → ∞ a n = lim ⁡ n → ∞ b n = 存 在 \color{maroon}[例1]\lbrace a_n\rbrace\downarrow,\lbrace b_n\rbrace\uparrow,\lim_{n\to\infty}(a_n-b_n)=0,证明\lim_{n\to\infty}a_n=\lim_{n\to\infty}b_n=存在\qquad\qquad\\ [例1]{an​}↓,{bn​}↑,n→∞lim​(an​−bn​)=0,证明n→∞lim​an​=n→∞lim​bn​=存在
$$\begin{gathered} [分析]由于\underset{n\to \infty }{\lim }(a_n-b_n)=0\exists ⟹A\le a_n-b_n\le B(极限若存在，数列必有界) \\ \therefore a_n\ge A+b_n\ge A+b下界b_n\le a_n-A\le a_1-A上界 \\ 由于极限存在，\underset{n\to \infty }{\lim }(a_n-b_n)=\underset{n\to \infty }{\lim }{a}_n-\underset{n\to \infty }{\lim }{b}_n=0 \end{gathered}$$
$$[例2]x_1=2,x_n+(x_n-4)x_{n-1}=3,n=2,3\dots ,证明\underset{n\to \infty }{\lim }{x}_n存在并求之$$
[ 分 析 ] { 1. x 1 = 2 , x 2 = 3 + 4 ⋅ 2 1 + 2 = 11 3 &gt; x 1 &gt; 0 2. 设 x k &gt; x k − 1 &gt; 0 3. 证 明 x k + 1 − x k = 3 + a x k 1 + x k − 3 + 4 x k − 1 1 + x k − 1 = x k − x k − 1 ( 1 + x k ) ( 1 + x k + 1 ) &gt; 0 &ThickSpace; ⟹ &ThickSpace; x k + 1 &gt; x k &gt; 0 &ThickSpace; ⟹ &ThickSpace; { x n } ↑ x n = 3 + 4 x n − 1 1 + x n − 1 = 4 + 4 x n − 1 − 1 1 + x n − 1 = 4 − 1 1 + x n − 1 &lt; 4 故 lim ⁡ n → ∞ x n = a &ThickSpace; ⟹ &ThickSpace; A = 3 + 4 A 1 + A &ThickSpace; ⟹ &ThickSpace; A = 3 ± 21 2 由 x n &gt; 0 &ThickSpace; ⟹ &ThickSpace; A ≥ 0 &ThickSpace; ⟹ &ThickSpace; A = 3 + 21 2 [分析]\begin{cases}1.x_1=2,x_2=\frac{3+4\cdot 2}{1+2}=\frac{11}3&gt;x_1&gt;0\\2.设x_k&gt;x_{k-1}&gt;0\\ 3.证明x_{k+1}-x_k=\frac{3+ax_k}{1+x_k}-\frac{3+4x_{k-1}}{1+x_{k-1}}=\frac{x_k-x_{k-1}}{(1+x_k)(1+x_{k+1})}&gt;0\implies x_{k+1}&gt;x_k&gt;0\implies\lbrace x_n\rbrace\uparrow\end{cases} \\x_n=\frac{3+4x_{n-1}}{1+x_{n-1}}=\frac{4+4x_{n-1}-1}{1+x_{n-1}}=4-\frac{1}{1+x_{n-1}}&lt;4\qquad\qquad\qquad\qquad\qquad\qquad\\ 故\lim_{n\to\infty}x_n=a\implies A=\frac{3+4A}{1+A}\implies A=\frac{3\pm\sqrt{21}}{2}\qquad\qquad\qquad\qquad\qquad\qquad\quad\\ 由x_n&gt;0\implies A\geq0\implies A=\frac{3+\sqrt{21}}{2}\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad [分析]⎩⎪⎨⎪⎧​1.x1​=2,x2​=1+23+4⋅2​=311​>x1​>02.设xk​>xk−1​>03.证明xk+1​−xk​=1+xk​3+axk​​−1+xk−1​3+4xk−1​​=(1+xk​)(1+xk+1​)xk​−xk−1​​>0⟹xk+1​>xk​>0⟹{xn​}↑​xn​=1+xn−1​3+4xn−1​​=1+xn−1​4+4xn−1​−1​=4−1+xn−1​1​<4故n→∞lim​xn​=a⟹A=1+A3+4A​⟹A=23±21 ​​由xn​>0⟹A≥0⟹A=23+21 ​​
$$[例3]a>0,x_n=\frac{a_n}{n!},n=1,2,\dots ,证明\underset{n\to \infty }{\lim }{x}_n存在并求之$$
[ 分 析 ] 显 然 x n &gt; 0 , x n + 1 x n = a n + 1 ( n + 1 ) ! ⋅ n ! a n = a n + 1      当 n + 1 &gt; a &gt; 0   即   n &gt; a − 1 时 ， a n + 1 &lt; 1 &ThickSpace; ⟹ &ThickSpace; x n + 1 x n &lt; 1 &ThickSpace; ⟹ &ThickSpace; x n + 1 &lt; x n &ThickSpace; ⟹ &ThickSpace; { x n } ↓ 得 lim ⁡ n → ∞ x n = A 且 x n + 1 = a n + 1 x n &ThickSpace; ⟹ &ThickSpace; A = 0 ⋅ A = 0 [分析]显然x_n&gt;0,\frac{x_{n+1}}{x_n}=\frac{a_{n+1}}{(n+1)!}\cdot\frac{n!}{a_n}=\frac a{n+1}\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\ \ \ \ \\ 当n+1&gt;a&gt;0\ 即\ n&gt;a-1时，\frac{a}{n+1}&lt;1\implies \frac{x_{n+1}}{x_n}&lt;1\implies x_{n+1}&lt;x_n\implies \lbrace x_n\rbrace\downarrow\\ 得\lim_{n\to\infty}x_n=A且x_{n+1}=\frac{a}{n+1}x_n\implies A=0\cdot A=0\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad [分析]显然xn​>0,xn​xn+1​​=(n+1)!an+1​​⋅an​n!​=n+1a​    当n+1>a>0 即 n>a−1时，n+1a​<1⟹xn​xn+1​​<1⟹xn+1​<xn​⟹{xn​}↓得n→∞lim​xn​=A且xn+1​=n+1a​xn​⟹A=0⋅A=0
$$\begin{gathered} [例4]设f(x)在[0,+\infty )上连续，0\le f(x)\le x_1,x\in [0,+\infty ),若a_1\ge 0,a_{n+1}=f(a_n),n=1,2,\dots \\ (Ⅰ)证明\underset{n\to \infty }{\lim }{a}_n存在，记为A，且A=f(A) \\ (Ⅱ)若条件改为0\le f(x)<x,x\in (0,+\infty ),求\underset{n\to \infty }{\lim }{a}_n \end{gathered}$$
[ 分 析 ] ( Ⅰ ) a n + 1 − a n = f ( a n ) − a n ≤ 0 , 显 然 a n + 1 = f ( a n ) ≥ 0 &ThickSpace; ⟹ &ThickSpace; a n + 1 ≤ a n &ThickSpace; ⟹ &ThickSpace; { a n } ↓   &ThickSpace; ⟹ &ThickSpace; lim ⁡ n → ∞ a n     存 在     → A = lim ⁡ n → ∞ f ( a n )     连 续     → f ( lim ⁡ n → ∞ a n ) = f ( A )        ( Ⅱ ) a n ≥ 0 &ThickSpace; ⟹ &ThickSpace; A ≥ 0 , 若 A &gt; 0 , f ( A ) &lt; A , 与 A = f ( A ) 矛 盾 ， 故 A = 0 &ThickSpace; ⟹ &ThickSpace; lim ⁡ n → ∞ a n = 0 [分析](Ⅰ)a_{n+1}-a_n=f(a_n)-a_n\leq0,显然a_{n+1}=f(a_n)\geq0\implies a_{n+1}\leq a_n\implies\lbrace a_n\rbrace\downarrow\qquad\ \\ \implies\lim_{n\to\infty}a_n\underrightarrow{\ \ \ 存在\ \ \ }A=\lim_{n\to\infty}f(a_n)\underrightarrow{\ \ \ 连续\ \ \ }f(\lim_{n\to\infty}a_n)=f(A)\qquad\qquad\qquad\qquad\\ \ \ \ \ \ \ (Ⅱ)a_n\geq0\implies A\geq0,若A&gt;0,f(A)&lt;A,与A=f(A)矛盾，故A=0\implies \lim_{n\to\infty}a_n=0 [分析](Ⅰ)an+1​−an​=f(an​)−an​≤0,显然an+1​=f(an​)≥0⟹an+1​≤an​⟹{an​}↓ ⟹n→∞lim​an​    存在   ​A=n→∞lim​f(an​)    连续   ​f(n→∞lim​an​)=f(A)      (Ⅱ)an​≥0⟹A≥0,若A>0,f(A)<A,与A=f(A)矛盾，故A=0⟹n→∞lim​an​=0

定义法

$$构造\mid x_n-a\mid ⟹x_n-a\to 0,即\underset{n\to \infty }{\lim }{x}_n=a\{\begin{array}{l}放缩法\\ 拉格朗日:f(b)-f(a)=f^{\prime }(\xi )(b-a)\end{array}$$
$$[例1]x_1\ge -12,x_{n+1}=\sqrt{12+x_n},n=1,2,\dots ,求\underset{n\to \infty }{\lim }{x}_n$$
$$\begin{gathered} [分析]若\underset{n\to \infty }{\lim }{x}_n=A,则A=\sqrt{12+A},则A=4 \\ 构造\mid x_n-4\mid =\mid \sqrt{12+x_{n-1}}-4\mid =\frac{\mid x_{n-1}\mid -4}{\sqrt{12+x_{n-1}}+4}\le \frac{1}{4}\mid x_{n-1}-4\mid \\ \le (\frac{1}{4}{)}^2\mid x_{n-2}-4\mid \\ \le (\frac{1}{4}{)}^{n-1}\mid x_1-4\mid \\ \underset{n\to \infty }{\lim }\mid x_n-4\mid =0⟹\underset{n\to \infty }{\lim }{x}_n=4 \end{gathered}$$
$$\begin{gathered} [例2]设f(x)在[a,b]上可导，\mid f^{\prime }(x)\mid \le \frac{1}{2},对x_0\in (a,b)有x_0=f(x_0),\forall x_1\in [a,b],x_{n+1}=f(x_n),n=1,2,\dots , \\ 证明\underset{n\to \infty }{\lim }{x}_n存在且\underset{n\to \infty }{\lim }{x}_n=x_0 \end{gathered}$$
$$\begin{gathered} [分析]\mid x_n-x_0\mid =\mid f(x_{n-1})-f(x_0)\mid =\mid f^{\prime }(\xi )\mid \mid x_{n-1}-x_0\mid \\ \le \frac{1}{2}\mid x_{n-1}-x_0\mid \\ \le (\frac{1}{2}{)}^2\mid x_{n-2}-x_0\mid \\ \le (\frac{1}{2}{)}^{n-1}\mid x_1-x_0\mid \\ ⟹\underset{n\to \infty }{\lim }{x}_n=x_0 \end{gathered}$$

夹逼准则

$$\begin{gathered} 定义\{\begin{array}{l}{y}_n\le x_n\le z_n(不验等号)\\ \downarrow \Downarrow \downarrow \\ A\to A\leftarrow A\end{array} \\ 考法\{\begin{array}{l}1.{\sum }_{i=1}^n{u}_i=u_1+u_2+\dots +u_n,n\to \infty ,则n\cdot u_{min}\le {\sum }_{i=1}^n{u}_i\le n\cdot u_{max}\\ 2.{\sum }_{i=1}^n{u}_i=u_1+u_2+\dots +u_n,n为有限数,u_1\ge 0,则1\cdot u_{max}\le {\sum }_{i=1}^n{u}_i\le n\cdot u_{max}\\ 3.有提示\end{array} \end{gathered}$$
$$[例1]\underset{n\to \infty }{\lim }(\frac{1}{\sqrt{n^2-1}}-\frac{1}{\sqrt{n^2-2}}-\frac{1}{\sqrt{n^2-3}}-\dots -\frac{1}{\sqrt{n^2-n}})$$
$$\begin{gathered} 原式=\underset{n\to \infty }{\lim }[\frac{1}{\sqrt{n^2-1}}-(\frac{1}{\sqrt{n^2-2}}+\frac{1}{\sqrt{n^2-3}}+\dots +\frac{1}{\sqrt{n^2-n}})] \\ \frac{n-1}{\sqrt{n^2-2}}<\sum _{i=2}^n\frac{1}{\sqrt{n^2-i}}<\frac{n-1}{\sqrt{n^2-n}} \\ \downarrow \Downarrow \downarrow \\ 1\to 1\leftarrow 1 \\ 而\underset{n\to \infty }{\lim }\frac{1}{\sqrt{n^2-1}}=0⟹I=0-1=-1 \end{gathered}$$
$$[例2]求f(x)=\underset{n\to \infty }{\lim }\sqrt[n]{1+x^n+(\frac{x^2}{2}{)}^n},x\ge 0$$
$$\begin{gathered} [分析]1.x\in [0,1)⟹1^n最大，\sqrt[n]{1\cdot 1^n}<\sqrt[n]{1+x^n+(\frac{x^2}{2}{)}^n}<\sqrt[n]{3\cdot 1^n} \\ \downarrow \Downarrow \downarrow \\ 1\to 1\leftarrow 1 \\ 2.x\in [1,2)⟹x^n最大 \\ 3.x\in [2,+\infty )⟹(\frac{x^2}{2})最大 \\ f(x)=\{\begin{array}{l}1,x\in [0,1)\\ x,x\in [1,2)\\ \frac{x^2}{2},x\in [2,+\infty )\end{array} \\ [注]\underset{\circ \to \infty }{\lim }\sqrt[n]{{\circ }^n+{\circ }^n+{\circ }^n},{\circ }_i\ge 0,有f(x)=\{\begin{array}{l}{f}_1,x\in I_1\\ f_2,x\in I_2\\ f_3,x\in I_3\end{array} \end{gathered}$$
$$\begin{gathered} [例3](Ⅰ)设f(x)=x^2,f[\varphi (x)]=-x^2+2x+3,且\varphi (x)\ge 0,求\varphi (x)及其定义域与值域 \\ (Ⅱ)求\underset{n\to \infty }{\lim }\frac{2020n}{n+\varphi (x)} \end{gathered}$$
$$\begin{gathered} [分析](Ⅰ)f[\varphi (x)]={\varphi }^2(x)=-x^2+2x+3,\because \varphi (x)\ge 0\therefore \varphi (x)=\sqrt{-x^2+2x+3} \\ \therefore 定义域为x\in [-1,3],值域为[0,2] \\ (Ⅱ)\frac{2020n}{n+2}\le \frac{2020n}{n+\varphi (x)}\le \frac{2020n}{n}=2020 \end{gathered}$$

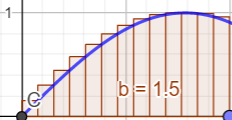
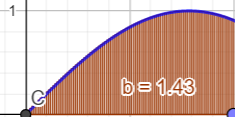
定积分定义法

定义

很早人们就发现了一个矩形的面积是$底\ast 高$，而一个边为曲线的图形呢？

黎曼（1826-1866）发现，将这种图形任意分割成n份，就可以粗略的看到一个个小矩形。

随着分割地越来越多，矩形也就变的越来越细。

一个矩形的面积是可以求得的，那么当这些矩形无限细的时候就可以通过求他们的面积和来得到曲边图形的面积，由于是黎曼最早提出的，定积分也叫做黎曼积分。

$$\begin{gathered} 1.[a,b]n等分，每段长度为\frac{b-a}{n} \\ 2.取右端点的高\to f(a+\frac{b-a}{n}i) \\ \therefore \underset{n\to \infty }{\lim }\sum _{i=1}^{n}f(a+\frac{b-a}{n}i)\frac{b-a}{n}={\int }_a^{b}f(x)dx \\ [小结] \\ 1.\underset{x\to \infty }{\lim }\sum _{i=1}^n=\underset{x\to \infty }{\lim }\sum _{i=0}^{n-1}（区别是前者取右端点，后者取左端点） \\ 2.\underset{x\to \infty }{\lim }\sum _{i=1}^{n}f(a+\frac{b-a}{n}i)\frac{b-a}{n}={\int }_a^{b}f(x)dx \\ 3.\underset{x\to \infty }{\lim }\sum _{i=1}^{n}f(0+\frac{1-0}{n}i)\frac{1-0}{n}={\int }_0^{1}f(x)dx \\ 4.\underset{x\to \infty }{\lim }\sum _{i=1}^{n}f(0+\frac{x-0}{n}i)\frac{x-0}{n}={\int }_0^{x}f(x)dx \end{gathered}$$
例题
$$\begin{gathered} [例1]求\underset{n\to \infty }{\lim }(\frac{1}{n+1}+\frac{1}{n+2}+\dots +\frac{1}{n+n}) \\ [分析]通式=\underset{n\to \infty }{\lim }\sum _{i=1}^n\frac{1}{n+i}=\underset{n\to \infty }{\lim }\sum _{i=1}^n\frac{1}{1+\frac{1}{n}}\cdot \frac{1}{n}={\int }_0^1\frac{1}{1+x}dx=\ln 2 \\ 对比:\underset{n\to \infty }{\lim }(\frac{n}{n^2+1}+\frac{n}{n^2+2}+\dots +\frac{n}{n^2+n}),其通式为\underset{n\to \infty }{\lim }\sum _{i=1}^n\frac{n}{n^2+i}=\underset{n\to \infty }{\lim }\sum _{i=1}^n\frac{n^2}{n^2+i}\cdot \frac{1}{n} \\ 应该用夹逼法则，\frac{n^2}{n^2+n}<\sum _{i=1}^n\frac{n}{n^2+i}<\frac{n^2}{n^2+1} \\ [例2]求\underset{n\to \infty }{\lim }(\frac{n+1}{n^2+1}+\frac{n+2}{n^2+4}+\frac{n+3}{n^2+9}+\dots +\frac{n+n}{n^2+n^2}) \\ [分析]通式=\underset{n\to \infty }{\lim }\sum _{i=1}^n\frac{n+i}{n^2+i^2}=\underset{n\to \infty }{\lim }\sum _{i=1}^n\frac{n^2+ni}{n^2+i^2}\cdot \frac{1}{n}=\underset{n\to \infty }{\lim }\sum _{i=1}^n\frac{1+(\frac{i}{n})}{1+(\frac{1}{n}{)}^2}\cdot \frac{1}{n}={\int }_0^1\frac{1+x}{1-x}dx=\frac{4}{\pi }+\frac{1}{2}\ln 2 \\ [例3]求\underset{n\to \infty }{\lim }(\frac{1}{\sqrt{n^2+n}}+\frac{1}{\sqrt{n^2+2n}}+\dots +\frac{1}{\sqrt{n^2+n^2}}) \\ [分析]通式=\underset{n\to \infty }{\lim }\sum _{i=1}^n\frac{1}{\sqrt{n^2+in}}=\underset{n\to \infty }{\lim }\sum _{i=1}^n\frac{1}{\sqrt{1+\frac{i}{n}}}\cdot \frac{1}{n}={\int }_0^1\frac{1}{\sqrt{1+x}}dx=2\sqrt{2}-2 \\ [例4]已知f(x)=a^{x^3},a>0且a̸=1,计算\underset{n\to \infty }{\lim }\frac{1}{n^4}\ln [f(1)f(2)\dots f(a)] \\ [分析]原式=\underset{n\to \infty }{\lim }\frac{1}{n^4}\ln (a^{1^3}\cdot a^{2^3}\cdot \dots \cdot a^{n^3})=\underset{n\to \infty }{\lim }\frac{1}{n^4}(1^3\ln a+2^3\ln a+\dots +n^3\ln a) \\ =\ln a\underset{n\to \infty }{\lim }\sum _{i=1}^n\frac{i^3}{n^4}=\ln a\underset{n\to \infty }{\lim }\sum _{i=1}^n(\frac{i}{n}{)}^3\cdot \frac{1}{n}=\ln a\cdot {\int }_0^1{x}^{3}dx=\frac{1}{4}\ln a \end{gathered}$$
$$\begin{gathered} [小结] \\ 能直接凑出\frac{i}{n}的基本形\{\begin{array}{l}1.n+i(an+bi)\\ 2.n^2+i^2\\ 3.n^2+ni\\ 4.\frac{i}{n}\end{array} \end{gathered}$$
$$\begin{gathered} [例5]求\underset{n\to \infty }{\lim }(\frac{1}{n+\frac{1}{n}}+\frac{1}{n+\frac{1+1}{n}}+\frac{1}{n+\frac{4+1}{n}}+\dots +\frac{1}{n+\frac{(n-1{)}^2+1}{n}}) \\ [分析]记x_n=\sum _{i=0}^{n-1}\frac{1}{n+\frac{i^2+1}{n}}=\sum _{i=0}^{n-1}\frac{1}{1+\frac{i^2+1}{n^2}}\cdot \frac{1}{n} \\ \because i^2<i^2+1<(i+1{)}^2 \\ \therefore \sum _{i=0}^{n-1}\frac{1}{1+(\frac{i+1}{n}{)}^2}\cdot \frac{1}{n}<x_n<\sum _{i=0}^{n-1}\frac{1}{1+(\frac{i}{n}{)}^2}\cdot \frac{1}{n} \\ \because \sum _{i=0}^{n-1}\frac{1}{1+(\frac{i+1}{n}{)}^2}\cdot \frac{1}{n}=\sum _{i=1}^n\frac{1}{1+(\frac{i}{n}{)}^2}\cdot \frac{1}{n} \\ \therefore 两边放缩，得：{\int }_0^1\frac{1}{1+x^2}dx=\frac{4}{\pi } \\ [小结] \\ 放缩法（凑不出\frac{i}{n}）\{\begin{array}{l}1.夹逼法则，如{\lim }_{n\to \infty }\frac{n}{n^2+1}+\frac{n}{n^2+2}+\dots +\frac{n}{n^2+n}=1\\ 2.放缩后再凑\frac{i}{n}，如上例\end{array} \end{gathered}$$
$$\begin{gathered} [例6]求\underset{n\to \infty }{\lim }(\frac{x}{n+x}+\frac{x}{n+2x}+\dots +\frac{x}{n+nx}),x>0 \\ 解：\underset{n\to \infty }{\lim }\sum _{i=1}^n\frac{x}{n+x\cdot i}=\underset{n\to \infty }{\lim }\sum _{i=1}^n\frac{1}{1+x\cdot \frac{i}{n}}\cdot \frac{x}{n}={\int }_0^x\frac{1}{1+t}dt=\ln (1+x) \\ [例7]求\underset{n\to \infty }{\lim }(sin\frac{x}{n}+sin\frac{2x}{n}+\dots +sinx)\frac{x}{n},x>0 \\ 解：\underset{n\to \infty }{\lim }\sum _{i=1}^{n}sin\frac{xi}{n}\cdot \frac{x}{n}={\int }_0^{x}sintdt=1-cosx \\ [小结] \\ 变量形：\underset{x\to \infty }{\lim }\sum _{i=1}^{n}f(0+\frac{x-0}{n}i)\frac{x-0}{n}={\int }_0^{x}f(x)dx \end{gathered}$$