OpenGL学习脚印: 模型变换(model transformation)

最新推荐文章于 2022-12-02 23:14:57 发布

fu_shuwu

最新推荐文章于 2022-12-02 23:14:57 发布

阅读量1.5k

点赞数

分类专栏： Opengl Android Linux 文章标签： model transformation opengl viewport

Android 同时被 3 个专栏收录

202 篇文章 2 订阅

订阅专栏

Linux

114 篇文章 1 订阅

订阅专栏

Opengl

25 篇文章 0 订阅

订阅专栏

http://blog.csdn.net/wangdingqiaoit/article/details/51531002

写在前面
前面为本节内容准备了向量和矩阵、线性变换等内容，本节开始学习OpenGL中的坐标处理。OpenGL中的坐标处理过程包括模型变换、视变换、投影变换、视口变换等内容，这个主题的内容有些多，因此分节学习，主题将分为5节内容来学习。本节主要学习模型变换。本节示例代码均可在我的github处下载。

通过本节可以了解到

模型变换的作用
模型变换的类型和计算方法

坐标处理的全局过程(了解，另文详述)

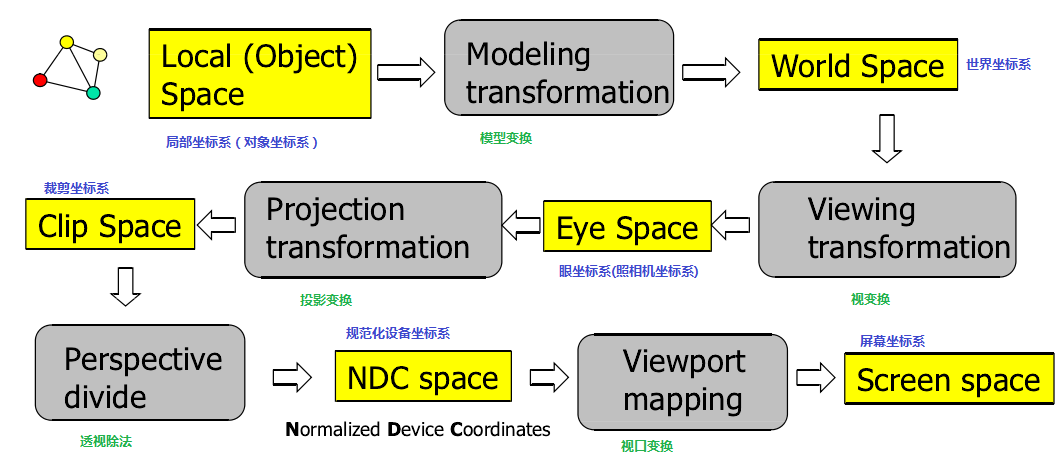
OpenGL中的坐标处理包括模型变换、视变换、投影变换、视口变换等内容，具体过程如下图1所示:

坐标变换
每一个过程处理都有其原因，这些内容计划将会在不同节里分别介绍，最后再整体把握一遍。
今天我们学习第一个阶段——模型变换。

为什么需要模型变换

我们在OpenGL中通过定义一组顶点来定义一个模型，或者通过其他3D建模软件事先建好模型然后导入到OpenGL中。顶点属性定义了模型。如果我们要在一个场景中不同位置显示同一个模型怎么办？如果我们要以不同的比例、不同角度显示同一个模型又怎么办？
如果继续以类似的顶点属性数据定义同一个模型，调整它满足上述需求的话，不仅浪费显卡内存，而且这个调整的工作量也很大，因此效率很低。更好地解决方法是，我们定义的模型根据需要可以执行放大、缩小等操作来不同比例显示，可以通过平移来放在不同位置，可以通过旋转来按不同角度显示。这种方式就是执行模型变换。
模型变换通过对模型执行平移(translation)、缩放(scale)、旋转(rotation)、镜像(reflection)、错切(shear)等操作，来调整模型的过程。通过模型变换，我们可以按照合理方式指定场景中物体的位置等信息。

平移变换

平移就是将物体从一个位置 p=(x,y,z) ，移动到另一个位置 p′=(x′,y′,z′) 的过程，记为 p′=p+d ，其中 d=(x′−x,y′−y,z′−z)=(tx,ty,tz) 。使用齐次坐标系表示为:

p' = T p = ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ 100001000010 t x t y t z 1 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ ⎡ ⎣ ⎢ ⎢ ⎢ x y z 1 ⎤ ⎦ ⎥ ⎥ ⎥ = ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ x + t x y + t y z + t z 1 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥

如果对向量和矩阵不熟悉，可以回过去看前面介绍的向量和矩阵；如果对上面使用的齐次坐标系不熟悉，可以回过去看前面介绍的线性变换部分。

本节的模型变换在OpenGL程序中，可以使用GLM数学库实现。例如平移变换实现如下：

glm::mat4 model; // 构造单位矩阵
model = glm::translate(model, glm::vec3(-0.5f, 0.0f, 0.0f));
 
 1
2
 
 1
2

上述表示平移向量为(-0.5,0.0,0.0)，得到一个平移矩阵存储到model中。

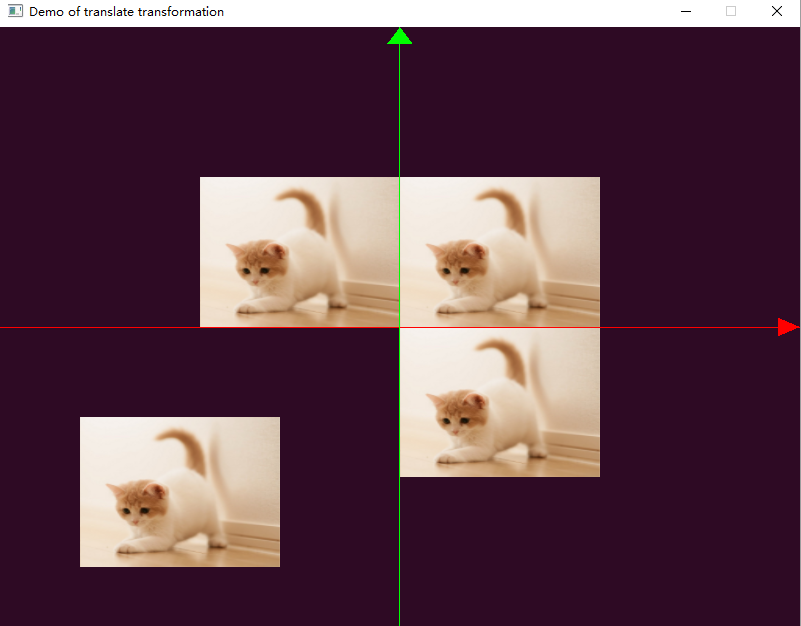
在程序中我们绘制了4个矩形，通过平移将其放在不同位置，效果如下图所示：
模型变换

在上图示例中，我们使用不同的着色器还绘制了坐标轴，坐标轴通过箭头和轴线绘制。在xoy坐标系中，第一个象限为原图，第二个象限为平移(-0.5,0.0,0.0)后的矩形,第三象限为平移(-0.8,-0.8,0.0)后的矩形，第四个象限为平移(0.0,-0.5,0.0)后的矩形。

注意通过上面坐标处理的全局过程图1可以看到，实际顶点输出还需要经过视变换、投影变换过程等处理，本节主要讨论模型变换，因此我们在代码中，不考虑视变换和投影变换，使用默认的视变换和投影变换，即这两个变换保持为单位矩阵。默认的方式就是我们一直在使用的正交投影方式。变换矩阵在着色器中使用uniform变量传递，在c++程序中使用glm::mat4与之对应。对uniform变量不熟悉的话，可以回过头去看2D纹理部分的使用方法。

设置默认视变换和投影变换矩阵的代码如下：

   glm::mat4 projection;// 投影变换矩阵
   glm::mat4 view; // 视变换矩阵
   glm::mat4 model; // 模型变换矩阵
   glUniformMatrix4fv(
     glGetUniformLocation(shader.programId,"projection"),
     1, GL_FALSE, glm::value_ptr(projection));  
  glUniformMatrix4fv(
    glGetUniformLocation(shader.programId,"view"),
    1,GL_FALSE, glm::value_ptr(view));
 
 1
2
3
4
5
6
7
8
9
 
 1
2
3
4
5
6
7
8
9

绘制四个矩形的代码为：

   // 绘制第一个矩形
   glUniformMatrix4fv(
    glGetUniformLocation(shader.programId, "model"),
    1, GL_FALSE, glm::value_ptr(model));
  glDrawElements(GL_TRIANGLES, 6, GL_UNSIGNED_SHORT, 0);

  // 绘制第二个矩形
 model = glm::mat4();
 model = glm::translate(model, glm::vec3(-0.5f, 0.0f, 0.0f));
glUniformMatrix4fv(
    glGetUniformLocation(shader.programId, "model"),
     1, GL_FALSE, glm::value_ptr(model));
glDrawElements(GL_TRIANGLES, 6, GL_UNSIGNED_SHORT, 0);

// 绘制第三个矩形
model = glm::mat4();
model = glm::translate(model, glm::vec3(-0.8f, -0.8f, 0.0f));
glUniformMatrix4fv(
  glGetUniformLocation(shader.programId, "model"),   1, GL_FALSE, glm::value_ptr(model));
glDrawElements(GL_TRIANGLES, 6, GL_UNSIGNED_SHORT, 0);

// 绘制第四个矩形
model = glm::mat4();
model = glm::translate(model, glm::vec3(0.0f, -0.5f, 0.0f));
glUniformMatrix4fv(
    glGetUniformLocation(shader.programId, "model"),1, GL_FALSE, glm::value_ptr(model));
glDrawElements(GL_TRIANGLES, 6, GL_UNSIGNED_SHORT, 0);
 
 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
 
 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

这里绘制矩形使用的顶点属性数据，以及纹理使用方法，可以回过头去查看上一节2D纹理映射内容。
本节绘制矩形的顶点着色器中都使用代码：

#version 330

layout(location = 0) in vec3 position;
layout(location = 1) in vec3 color;
layout(location = 2) in vec2 textCoord;

out vec3 VertColor;
out vec2 TextCoord;

uniform mat4 projection;
uniform mat4 view;
uniform mat4 model;

void main()
{
     gl_Position = 
     projection * view * model * vec4(position, 1.0);
     VertColor = color;
     TextCoord = textCoord;
}
 
 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
 
 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

本节绘制矩形的片元着色器中都使用代码：

#version 330

in vec3 VertColor;
in vec2 TextCoord;

uniform sampler2D tex;

out vec4 color;


void main()
{
  color = texture(tex, vec2(TextCoord.s, 1.0 -TextCoord.t) );
}
 
 1
2
3
4
5
6
7
8
9
10
11
12
13
14
 
 1
2
3
4
5
6
7
8
9
10
11
12
13
14

代码中使用坐标vec2(TextCoord.s, 1.0 -TextCoord.t)表示将纹理的y轴翻转，避免纹理倒立显示。
在坐标和变换的数学基础一节中，我们已经提到，对于4x4仿射变换矩阵，可以表示平移(仿射变换)、缩放、旋转等线性变换，其中矩阵的形式为：

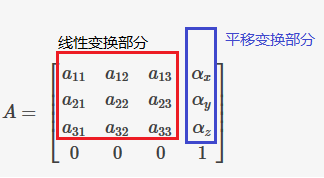
记住这一点，对于矩阵形式理解会比较清楚。

缩放变换

缩放可以沿着三个坐标轴的方向独立进行，当缩放参数一致时是均匀缩放，否则是非均匀缩放。对于以原点为中心的缩放来讲，根据坐标和变换的数学基础，一节所得到的结论：线性变换矩阵为变换后基向量组成。缩放因子为 (sx,sy,sz) ，则得到缩放后的+x轴基向量为 (sx,0,0) ，+y轴基向量为 (0,sy,0) ，+z轴缩放后基向量为 (0,0,sz) ，由这些基向量组成的缩放矩阵的前三列，构成4x4矩阵后表示为:

p' = S p = ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ s x 000 0 s y 00 00 s z 0 0001 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ ⎡ ⎣ ⎢ ⎢ ⎢ x y z 1 ⎤ ⎦ ⎥ ⎥ ⎥ = ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ x * s x y * s y z * s z 1 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥

注意设一个方向的缩放因子为 k ，当 k>0 表示物体变长；当 k=0 时表示正交投影，此时有一些维度的信息变为0了；当 k<0 时物体将会发射，即发生镜像变换，后面会介绍镜像变换。

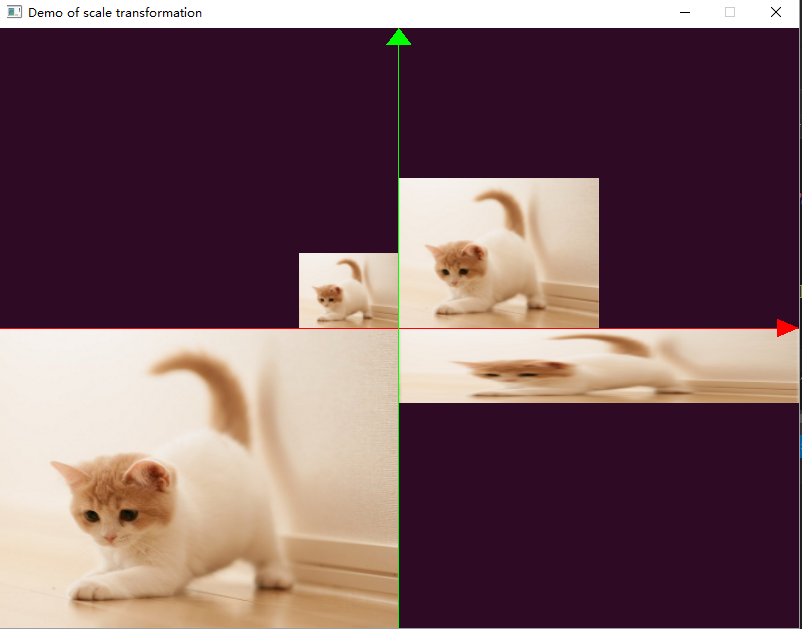
执行缩放变换，效果如下图所示：

上图中，第一象限为原图，第二象限为均匀缩放0.5倍，然后平移(-0.25, 0.0,0.0)后的结果；第三象限为均匀缩放2.0倍，然后平移(-1.0, -1.0,0.0)后的结果；第四象限为缩放(2.0,0.5,1.0)后，平移(0.0,-0.25,0.0)后的结果。例如第四象限使用的代码为：

// 绘制第四个矩形 x轴放大两倍 y轴缩小为一半 平移到第四象限
model = glm::mat4();
model = glm::translate(model, glm::vec3(0.0f, -0.25f, 0.0f));
model = glm::scale(model, glm::vec3(2.0f, 0.5f, 1.0f));
glUniformMatrix4fv(
    glGetUniformLocation(shader.programId, "model"),
    1, GL_FALSE, glm::value_ptr(model));
glDrawElements(GL_TRIANGLES, 6, GL_UNSIGNED_SHORT, 0);
 
 1
2
3
4
5
6
7
8
 
 1
2
3
4
5
6
7
8

这里需要注意几点:
(1) 模型变换进行的顺序与结果是相关的。在向量和矩阵一节已经讲过，矩阵乘法不满足交换律，即 AB≠BA ，因此变换的顺序会影响最终结果。
(2) 上述第四个象限矩形，先进行缩放，然后平移到第四象限，这个过程表示为 p′=T∗S∗p ，根据结合了，可以写为 p′=(T∗S)p=Mp ，即只需要在CPU中计算出最终的变换矩阵M即可，而不是在顶点着色器中完成矩阵乘法。
(3)上述代码中，要按照先缩放后平移来完成模型变换，代码书写的顺序和我们变换的顺序是相反的，主要原因是:

model = glm::mat4();
model = glm::translate(model, glm::vec3(0.0f, -0.25f, 0.0f));
model = glm::scale(model, glm::vec3(2.0f, 0.5f, 1.0f));
 
 1
2
3
 
 1
2
3

这个代码等价于:

translate = glm::translate(glm::mat4(), glm::vec3(0.0f, -0.25f, 0.0f));
scale = glm::scale(glm::mat4(), glm::vec3(2.0f, 0.5f, 1.0f));
model = translate * scale
 
 1
2
3
 
 1
2
3

也就是说glm::scale是对单位矩阵进行缩放，然后左乘平移矩阵。这一点尤其要注意。

旋转变换

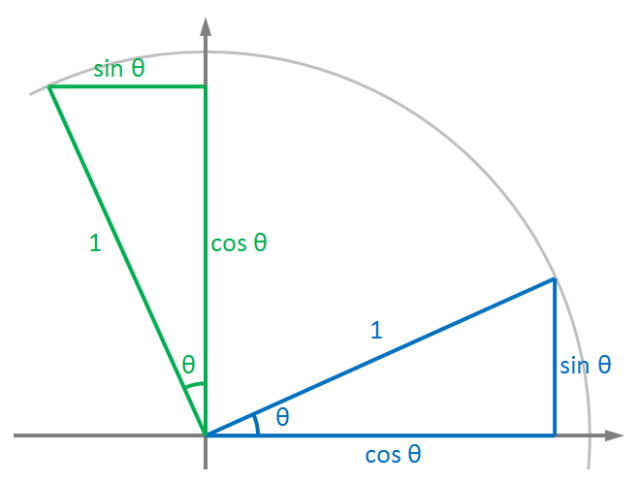
对于以原点为中心的旋转来讲，旋转矩阵可以这样来推导。以下面的绕+z轴的旋转角度 θ 为例，从xoy轴角度来看如下图所示：

这样经过旋转以后，原来的+x轴对应的基向量 (1,0,0) 变为 (cosθ,sinθ,0) ；原来的+y轴对应的基向量 (0,1,0) 变为 (−sinθ,cosθ,0) ；而+z轴保持不变，为 (0,0,1) ，由三个变换后的基向量构成旋转矩阵的前三列，以4x4矩阵形式书写为：

R z (θ) = ⎡ ⎣ ⎢ ⎢ ⎢ c o s θ s i n θ 00 - s i n θ c o s θ 00 00100001 ⎤ ⎦ ⎥ ⎥ ⎥

对于绕y轴，x轴的旋转同理可得到旋转矩阵如下:

R y (θ) = ⎡ ⎣ ⎢ ⎢ ⎢ c o s θ 0 - s i n θ 0 0100 s i n θ 0 c o s θ 0 0001 ⎤ ⎦ ⎥ ⎥ ⎥

R x (θ) = ⎡ ⎣ ⎢ ⎢ ⎢ 1000 0 c o s θ s i n θ 0 0 - s i n θ c o s θ 0 0001 ⎤ ⎦ ⎥ ⎥ ⎥

不动点与旋转和缩放

对于旋转和缩放来说，我们上面得出的矩阵，都是针对物体以原点为中心进行的旋转和缩放，这种中心点称为不动点 pf 。对于不动点不再原点的旋转，获取旋转矩阵的思路是：先把物体的中心移到原点，然后应用上面的旋转矩阵，最后再把物体移回到原处，使得它的中心仍旧位于 pf 。这一过程表示为:
M=T(pf)R(θ)T(−pf)(旋转中心问题)
对于缩放的缩放中心也有类似处理。

执行旋转变换，效果如下图所示：

其中，第一象限为原图，第二象限为绕+z轴旋转90度；第三象限为以中心点(0.25,0.25,0.0)旋转，平移(-0.5,-0.5,0.0)到第三象限的结果；第四象限为绕着右下角(0.5,0.0,0.0)旋转，平移(0.0, -0.5,0.0)到第四象限的结果。例如第三象限的绘制代码为：

// 绘制第三个矩形 绕着矩形中心旋转
model = glm::mat4();
// 平移至第三象限
model = glm::translate(model, glm::vec3(-0.5f, -0.5f, 0.0f)); 
// 下面为绕着中心旋转的三个矩阵
model = glm::translate(model, glm::vec3(0.25f, 0.25f, 0.0f));
model = glm::rotate(model, (GLfloat)glfwGetTime() * 2.0f,
            glm::vec3(0.0f, 0.0f, 1.0f));
model = glm::translate(model, glm::vec3(-0.25f, -0.25f, 0.0f)); 
glUniformMatrix4fv(
    glGetUniformLocation(shader.programId, "model"),
    1, GL_FALSE, glm::value_ptr(model));
glDrawElements(GL_TRIANGLES, 6, GL_UNSIGNED_SHORT, 0);
 
 1
2
3
4
5
6
7
8
9
10
11
12
13
 
 1
2
3
4
5
6
7
8
9
10
11
12
13

注意上面代码中，为了实现绕着矩形中心(0.25,0.25,0.0)旋转，先要平移至原点，然后旋转，最后平移至中心；为了实现平移至第三象限，实行平移变换(-0.5,-0.5,0.0)。

镜像变换

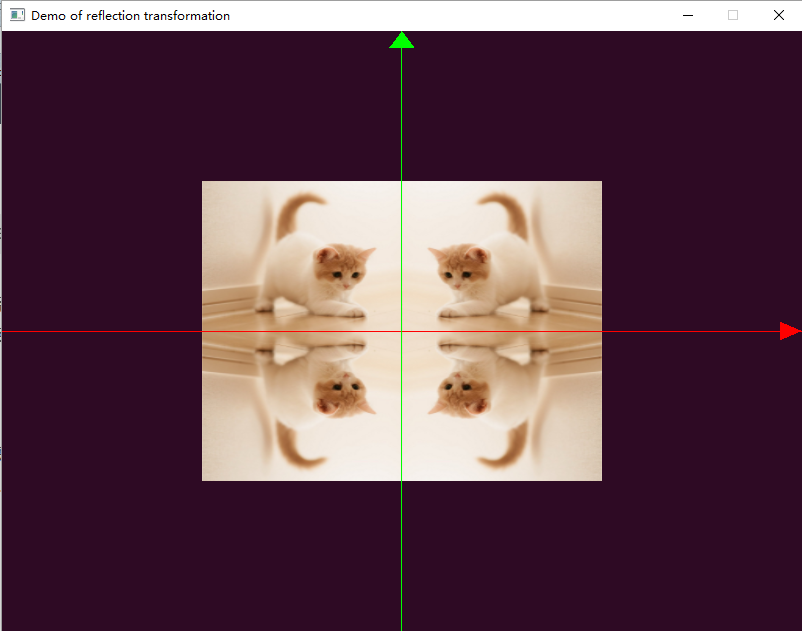
镜像变换，就是反射成像的概念，它是缩放变换的一个特例，当缩放因子 k<0 时会导致镜像变换。执行镜像变换后的效果如下图所示：

上面图中，第一象限为原图，第二象限为关于y轴的镜像，即点 (x,y,z) 镜像后点为 (−x,y,z) ，因此所求矩阵为:

R e f l e c t y = ⎡ ⎣ ⎢ ⎢ ⎢ - 1 000 010000100001 ⎤ ⎦ ⎥ ⎥ ⎥

可以看出这个矩阵，就是上面的缩放矩阵，当缩放因子为(-1.0,1.0,1.0)时的矩阵。因此实现时代码为：

   // 绘制第二个矩形 沿着y轴镜像
model = glm::mat4();
model = glm::scale(model, glm::vec3(-1.0f, 1.0f, 1.0f));
glUniformMatrix4fv(
    glGetUniformLocation(shader.programId, "model"),
    1, GL_FALSE, glm::value_ptr(model));
glDrawElements(GL_TRIANGLES, 6, GL_UNSIGNED_SHORT, 0);
 
 1
2
3
4
5
6
7
 
 1
2
3
4
5
6
7

上图中，第三象限为以xy轴同时反射形成，缩放因子为(-1.0,-1.0,1.0)；第四象限为以x轴进行反射，缩放因子为(1.0, -1.0, 1.0)。

应用变换的顺序问题

前面提到过由于矩阵乘法不满足交换律，即 AB≠BA ，因此变换的顺序会影响最终结果。例如下面图中（来自World, View and Projection Transformation Matrices），上面部分所示为先绕着+y轴旋转90度，然后沿着x轴平移后的效果；下面部分所示，为先沿着X轴平移，然后绕着+y轴旋转90度后的效果。这两者的结果是不同的。
变换顺序
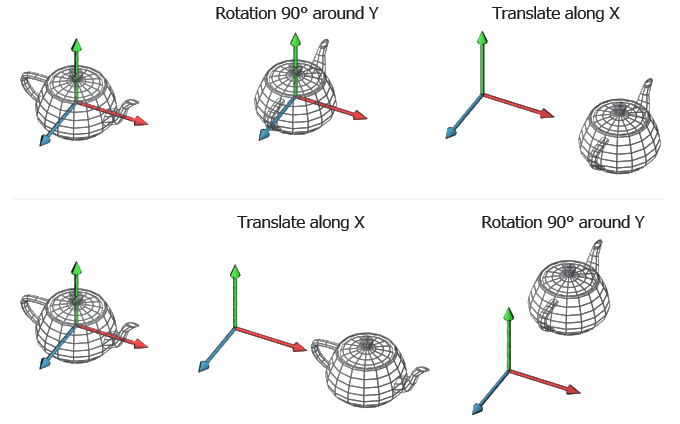
假设茶壶嘴的接口上一点坐标原始为 p=（1,0,0,1），沿着x轴平移部分为2个单位。
则图中上半部分执行过程为：
Step1 ：先绕着+y轴旋转90度，

p' = R p = ⎡ ⎣ ⎢ ⎢ ⎢ 00 - 1 0 010010000001 ⎤ ⎦ ⎥ ⎥ ⎥ * ⎡ ⎣ ⎢ ⎢ ⎢ 1001 ⎤ ⎦ ⎥ ⎥ ⎥ = ⎡ ⎣ ⎢ ⎢ ⎢ 00 - 1 1 ⎤ ⎦ ⎥ ⎥ ⎥

Step2 ：沿着x轴平移2个单位，

p'' = T p' = ⎡ ⎣ ⎢ ⎢ ⎢ 1000010000102001 ⎤ ⎦ ⎥ ⎥ ⎥ * ⎡ ⎣ ⎢ ⎢ ⎢ 00 - 1 1 ⎤ ⎦ ⎥ ⎥ ⎥ = ⎡ ⎣ ⎢ ⎢ ⎢ 20 - 1 1 ⎤ ⎦ ⎥ ⎥ ⎥

得到最终点p结果为(2,0,-1,1)。

而则图中下半部分执行过程为：

Step1 ：先沿着x轴平移2个单位，

p' = T p = ⎡ ⎣ ⎢ ⎢ ⎢ 1000010000102001 ⎤ ⎦ ⎥ ⎥ ⎥ * ⎡ ⎣ ⎢ ⎢ ⎢ 1001 ⎤ ⎦ ⎥ ⎥ ⎥ = ⎡ ⎣ ⎢ ⎢ ⎢ 3001 ⎤ ⎦ ⎥ ⎥ ⎥

Step2 ：再绕着+y轴旋转90度，

p'' = R p' = ⎡ ⎣ ⎢ ⎢ ⎢ 00 - 1 0 010010000001 ⎤ ⎦ ⎥ ⎥ ⎥ * ⎡ ⎣ ⎢ ⎢ ⎢ 3001 ⎤ ⎦ ⎥ ⎥ ⎥ = ⎡ ⎣ ⎢ ⎢ ⎢ 00 - 3 1 ⎤ ⎦ ⎥ ⎥ ⎥

得到最终点p结果为(0,0,-3,1)。
可以看到执行顺序不同，应用相同的变换矩阵，结果是不一样的。导致结果不同的原因在于，图中上半部分在绕着+y轴旋转90度后，茶壶的x轴发生变化，而应用变换矩阵时沿着的x轴是全局的，是之前的x轴，而不是变换后的x轴，因此导致两者结果不一样。这一点需要引起注意。

最后说明

上面讨论的模型变换部分涉及到了平移、缩放、旋转和镜像变换，在实际中多半是这些变换的组合，一般地执行变换顺序为缩放–》旋转—》平移。在实行模型变换时，要注意变换的顺序和代码中书写的顺序相反。同时对于缩放和旋转变换，要注意不动点不在原点时的处理方法。对于绕任意方向的旋转，需要推导一个新的旋转矩阵，这个内容会放在数学相关的小节介绍。