神经网络——bias 偏置项（bias term） 或者截距项（intercept term）

神经网络——bias 偏置项（bias term）或者截距项（intercept term）

参考文献

神经网络——bias_神经网络参数网w,b的名字_Devin01213的博客-CSDN博客

神经网络中，bias有什么用，为什么要设置bias，当加权和大于某值时，激活才有意义？ - 知乎

1、什么是bias？

偏置单元（bias unit），在有些资料里也称为偏置项（bias term）或者截距项（intercept term），它其实就是函数的截距，与线性方程 y=wx+b 中的 b 的意义是一致的。

在 y=wx+b中，b表示函数在y轴上的截距，控制着函数偏离原点的距离，其实在神经网络中的偏置单元也是类似的作用。

因此，神经网络的参数也可以表示为：(W, b)

W表示参数矩阵，

b表示偏置项或截距项。

2、bias的计算方式？

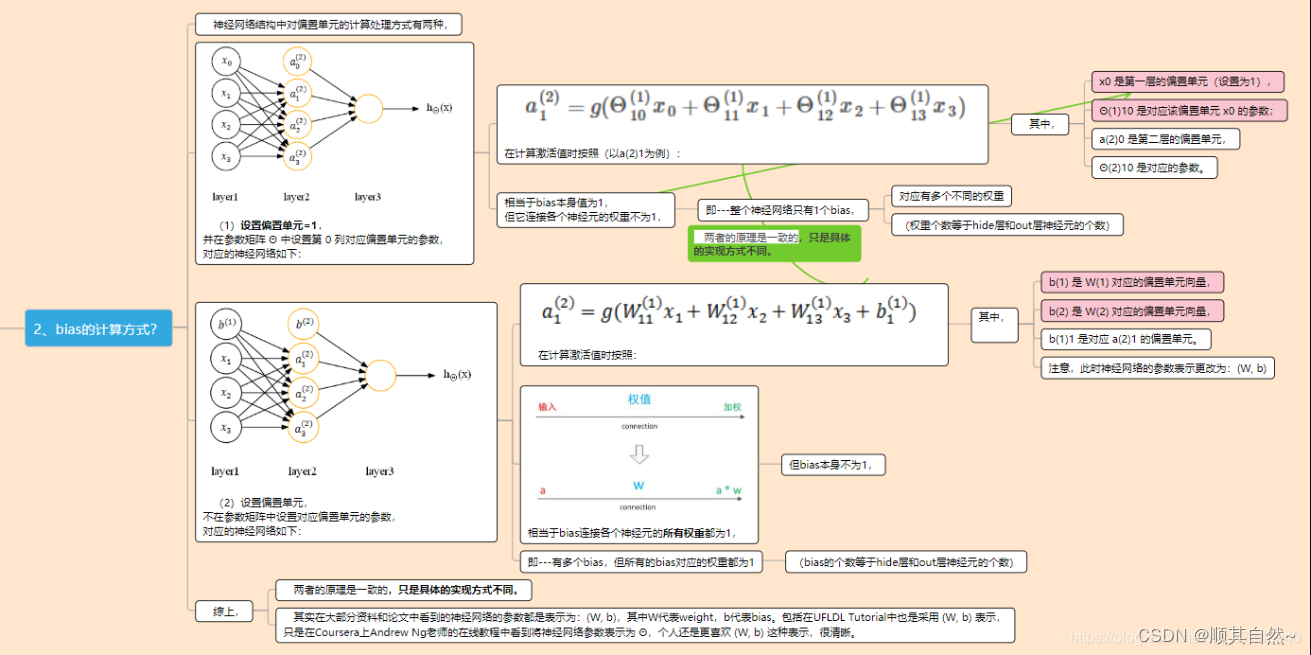
神经网络结构中对偏置单元的计算处理方式有两种，

（1）设置偏置单元=1，并在参数矩阵 中设置第 0 列对应偏置单元的参数，对应的神经网络如下：

在计算激活值时按照（以a(2)1为例）：

其中，

x0 是第一层的偏置单元（设置为1），

(1)10 是对应该偏置单元 x0 的参数；

a(2)0 是第二层的偏置单元，

(2)10 是对应的参数。

相当于bias本身值为1，但它连接各个神经元的权重不为1，

即—整个神经网络只有1个bias，

对应有多个不同的权重

（权重个数等于hide层和out层神经元的个数）

（2）设置偏置单元，不在参数矩阵中设置对应偏置单元的参数，对应的神经网络如下：

在计算激活值时按照：

其中，

b(1) 是 W(1) 对应的偏置单元向量，

b(2) 是 W(2) 对应的偏置单元向量，

b(1)1 是对应 a(2)1 的偏置单元。

注意，此时神经网络的参数表示更改为：(W, b)

相当于bias连接各个神经元的所有权重都为1，

但bias本身不为1，

即—有多个bias，但所有的bias对应的权重都为1

（bias的个数等于hide层和out层神经元的个数）

综上，

两者的原理是一致的，只是具体的实现方式不同。

其实在大部分资料和论文中看到的神经网络的参数都是表示为：(W, b)，其中W代表weight，b代表bias。包括在UFLDL Tutorial中也是采用 (W, b) 表示，只是在Coursera上Andrew Ng老师的在线教程中看到将神经网络参数表示为 Θ，个人还是更喜欢 (W, b) 这种表示，很清晰。

卷积之后，如果要接BN操作，最好是不设置偏置，因为不起作用，而且占显卡内存。

BN操作，里面有一个关键操作

其中x1 = x0 * w0 + b0，而E[x1] = E[x0*w0] + b0， 所以对于分子而言，加没加偏置，没有影响；

而对于下面分母而言，因为Var是方差操作，所以也没有影响（为什么没影响，回头问问你的数学老师就知道了）。

所以，

卷积之后，如果要接BN操作，

最好是不设置偏置，

因为不起作用，而且占显卡内存。

神经网络中，加上bias是如何让网络变得更灵活

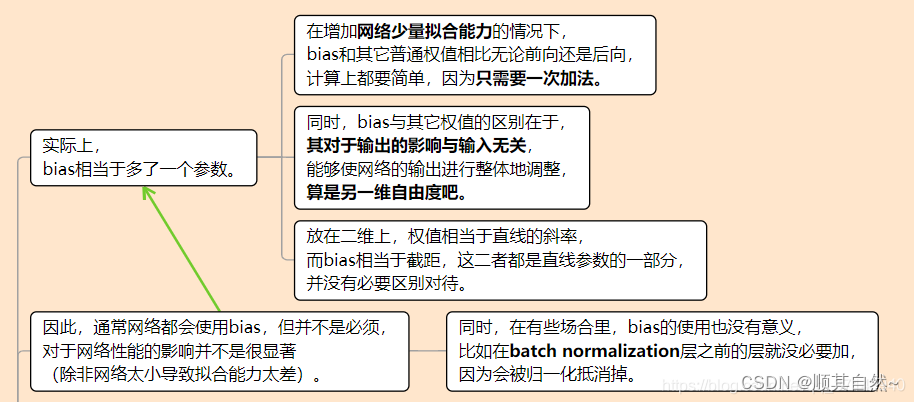
实际上，bias相当于多了一个参数。

在增加网络少量拟合能力的情况下，bias和其它普通权值相比无论前向还是后向，计算上都要简单，因为只需要一次加法。

同时，bias与其它权值的区别在于，其对于输出的影响与输入无关，能够使网络的输出进行整体地调整，算是另一维自由度吧。

放在二维上，权值相当于直线的斜率，而bias相当于截距，这二者都是直线参数的一部分，并没有必要区别对待。

因此，通常网络都会使用bias，但并不是必须，对于网络性能的影响并不是很显著（除非网络太小导致拟合能力太差）。

同时，在有些场合里，bias的使用也没有意义，比如在batch normalization层之前的层就没必要加，因为会被归一化抵消掉。

简单考虑一个只有一输入一输出的简单网络：

假设用Sigmoid 激活函数，如果没有bias，先看一下在不同W下的情况：

假如输入 X_{in} 的输入分布如图中蓝点（A集合）和红点（B集合）所示（在x轴上的分布），要通过 Y_{out}(>0.5, or <0.5) 来判断输入时在A内还是B内，很显然，要提高准确性，sigmoid函数中的W系数需要学的很大，才能保证尽可能的判断准确。

但是如果一个测试样本在图中绿点所在的位置呢，很明显我们可以将绿点判为红点所在的B集合，但是通过训练学到的W是不能正确判断的。

这个时候似乎让sigmoid函数变得更陡没法解决了。

但是如果加一个bias呢。

像这样，w（sigmoid中x的系数）不用学的很大就可以提高学习的准确率，网络就能够非常灵活的fit A,B 的分布，可以准确的判断绿点所属的集合。

简单点说，就是加上bias能更灵活的fit输入的分布。

（1）设置偏置单元=1，并在参数矩阵 Θ 中设置第 0 列对应偏置单元的参数，对应的神经网络如下：

其中，x0 是第一层的偏置单元（设置为1），Θ(1)10 是对应该偏置单元 x0 的参数；a(2)0 是第二层的偏置单元，Θ(2)10 是对应的参数。 

在计算激活值时按照（以a(2)1为例）： 

相当于bias本身值为1，但它连接各个神经元的权重不为1，即---整个神经网络只有1个bias，对应有多个不同的权重（权重个数等于hide层和out层神经元的个数）

（2）设置偏置单元，不在参数矩阵中设置对应偏置单元的参数，对应的神经网络如下：

其中，b(1) 是 W(1) 对应的偏置单元向量，b(2) 是 W(2) 对应的偏置单元向量，b(1)1 是对应 a(2)1 的偏置单元。注意，此时神经网络的参数表示更改为：(W, b) 

在计算激活值时按照：  

相当于bias连接各个神经元的所有权重都为1，但bias本身不为1，即---有多个bias，但所有的bias对应的权重都为1（bias的个数等于hide层和out层神经元的个数）

综上， 

两者的原理是一致的，只是具体的实现方式不同。 

其实在大部分资料和论文中看到的神经网络的参数都是表示为：(W, b)，其中W代表weight，b代表bias。包括在UFLDL Tutorial中也是采用 (W, b) 表示，只是在Coursera上Andrew Ng老师的在线教程中看到将神经网络参数表示为 Θ，个人还是更喜欢 (W, b) 这种表示，很清晰。 

转自：【思维导图】神经网络——bias 偏置项（bias term） 或者截距项（intercept term）_截距项是什么_认知计算_茂森的博客-CSDN博客