一、平面极坐标系定义
1. 定义
在参考系上取一点 O O O 称为极点，由 O O O 点引一有刻度的射线，称之为极轴，即构成极坐标系。
2. 极坐标系
质点的位置 P P P 由极径 ρ \rho ρ 和幅角 θ \theta θ 给出。如下图所示。
ρ \rho ρ ：极径，极点到质点的距离
θ \theta θ：幅角或极角，极径与极轴的夹角，规定角度取逆时针方向为正
3. 正交单位矢量
- 径向单位矢量 i \bm{i} i ：方向从极点指向质点。则矢径 r = ρ i \bm{r} = \rho \bm{i} r=ρi。
- 横向单位矢量 j \bm{j} j ：方向与径向单位矢量垂直，且指向 θ \theta θ 增加的方向。
4. 正交单位矢量对时间 t 的导数的计算
设初始时刻质点位置为 P 1 P_{1} P1，经过时间 d t dt dt，质点位置为 P 2 P_{2} P2，幅角变化量为 d θ d\theta dθ。如下图所示。
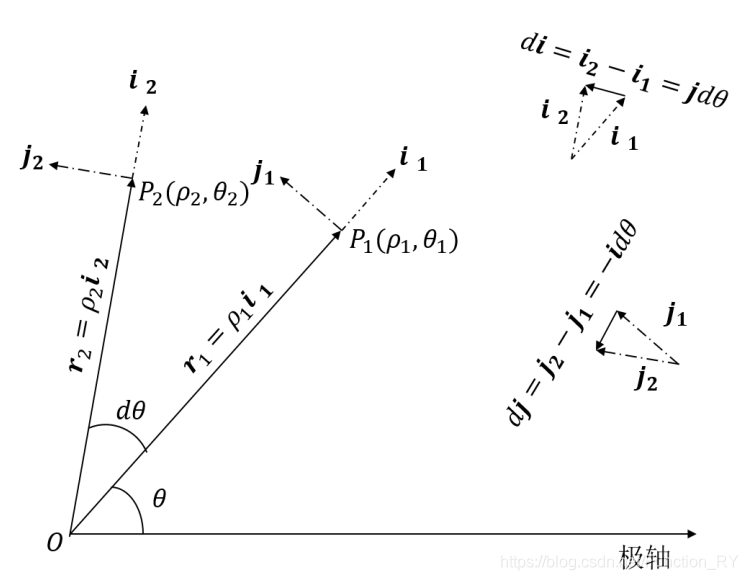
4.1 径向单位矢量 i \bm{i} i
经过时间 d t dt dt，径向单位矢量由 i 1 \bm{i}_{1} i1变化到 i 2 \bm{i}_{2} i2，转过的角度为 d θ d\theta dθ。
d i = i 2 − i 1 d\bm{i}=\bm{i}_{2}-\bm{i}_{1} di=i2−i1
由于 i \bm{i} i为单位矢量，且 d t dt dt为趋于 0 0 0的微元。所以 d i d\bm{i} di的大小即为以 ∣ i ∣ |\bm{i}| ∣i∣为半径，角度为 d θ d\theta dθ所对应的弧长（单位矢量 i \bm{i} i从 i 1 \bm{i}_{1} i1旋转到 i 2 \bm{i}_{2} i2时，箭头末端所经过的路程），其大小为：
∣ d i ∣ = ∣ i ∣ ⋅ d θ = d θ |d\bm{i}|=|\bm{i}|\cdot d\theta=d\theta ∣di∣=∣i∣⋅dθ=dθ
d i d\bm{i} di的方向为从 i 1 \bm{i}_{1} i1的末端指向 i 2 \bm{i}_{2} i2的末端，当 d t dt dt趋于 0 0 0时， d i d\bm{i} di的方向垂直于 i \bm{i} i并且指向 θ \theta θ的增加方向，所以 d i d\bm{i}
最低0.47元/天 解锁文章
2152
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
