数学 - 泰勒公式，常见麦克劳林公式及Maple函数拟合

数学 - 泰勒公式，常见麦克劳林公式及Maple函数拟合

---

泰勒公式可以将一个函数在某点展开成多项式函数的形式，通常可用于近似计算。多项式函数是最简单的一类函数，将复杂函数转换成多项式函数可简化对原始函数的研究，求导，求积分都比较方便。麦克劳林公式是泰勒公式在x=0处的展开形式，是泰勒公式的简化版和特例。

泰勒公式：

若函数 f(x) 在包含的某个闭区间[a,b]上具有n阶导数，且在开区间（a,b）上具有（n+1）阶导数，则对闭区间[a,b]上任意一点x，成立下式：

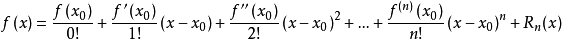
上面的多项式称为 f(x) 在点处的泰勒展开式，该公式为泰勒公式。

特别的，当泰勒公式中取0的时候，若f(x)在x=0处n阶连续可导，则下式成立：

该公式称为为麦克劳林公式。

研究泰勒公式（麦克劳林公式）的意义在于其可以将任意一个函数转换成多项式函数的近似表达，这样就能用多项式函数来拟合原函数。

---

常见麦克劳林公式：

指数函数：

 

 

自然对数：

 

 

正弦函数：

 

余弦函数：

Maple函数拟合：

下面通过Mapl来求麦克劳林展开式，及绘制相关的函数图像。

sin(x)

cos(x)

 

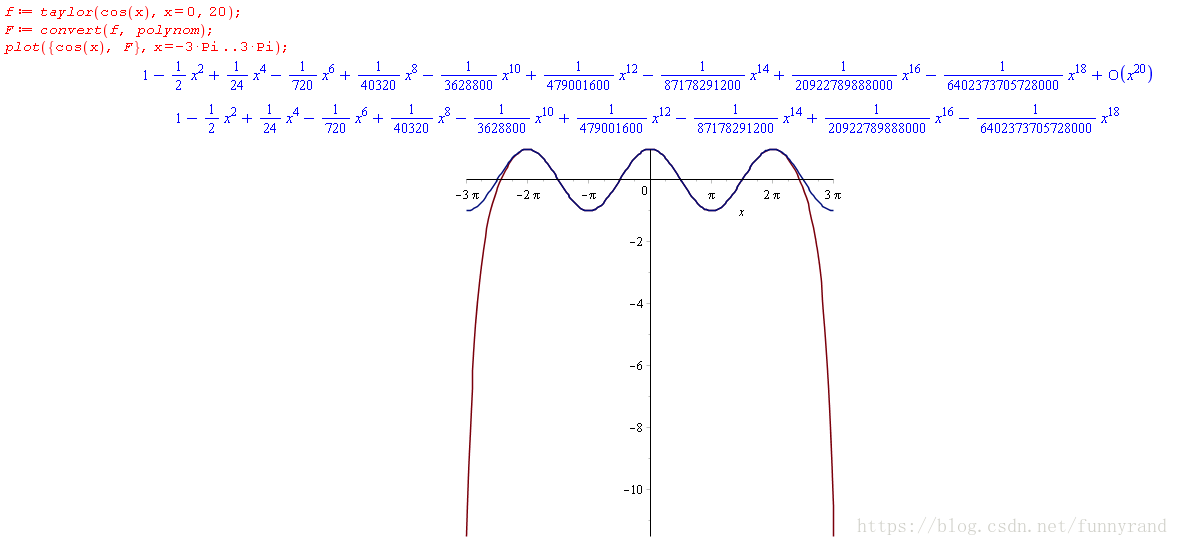
ln(1+x)

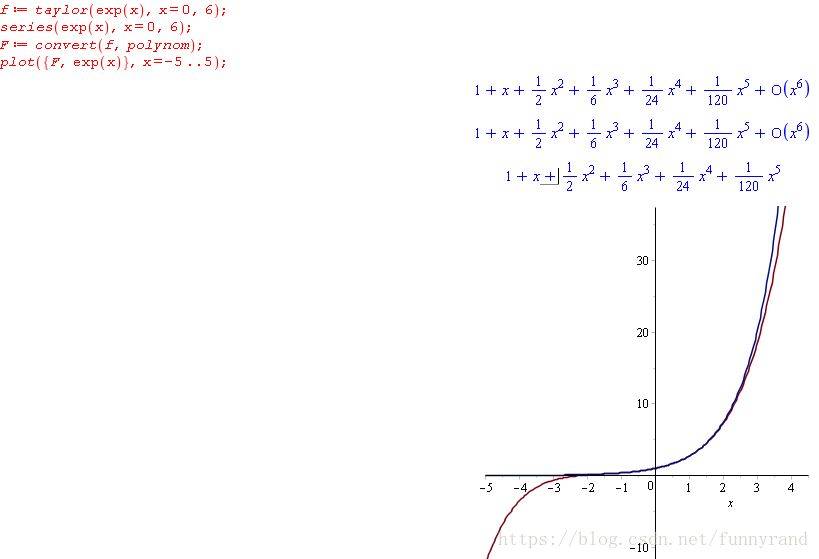
exp(x)

1/(1-x)