问题描述:
已知一个全局坐标系,还有若干局部坐标系,如何将局部坐标系的坐标转成全局坐标系的坐标?反过来又如何进行?
这里的坐标系都是直角坐标系。
本文通过下面几个方面的研究来回答上面的问题。
1、简单示例
2、求解过程
3、nodejs编程验证
简单示例
已知点A(6,6),B(14,14),C(-2,14),G(12,12),求当A为原点 ,AB为X轴,AC为Y轴时 G点的坐标。可以见下图:

通过查看图形,我们可以很快的计算出点G新的坐标如下:
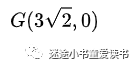
但是如果G为任意一点,我们还能轻松求出来么?显然我们不行。我们需要一种通用的方法来一次到位,这里就引入了矩阵变换的概念。
求解过程
重新理解坐标系的(x,y)。看下图:
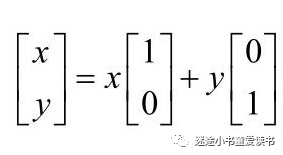
我们的某个点的坐标实际上表达的是坐标轴单位向量的个数。x表示X轴单位向量个数,y表示Y轴单位向量个数。有了这个概念之后,我们重新来看待上面的问题:
假设AB单位向量为p(px,py),AC单位向量为q(qx,qy)。点G在新坐标系下为(x1,y1)
 坐标变换与矩阵运算:从局部到全局坐标系
坐标变换与矩阵运算:从局部到全局坐标系





 本文介绍了如何通过矩阵变换将局部坐标系的坐标转换为全局坐标系,反之亦然。首先,通过一个简单的示例解释坐标变换的直观理解,然后详细阐述坐标实际表示坐标轴单位向量的数量。接着,利用node.js编程验证了变换矩阵的正确性,通过构建三维变换矩阵实现一步到位的坐标转换。最后,通过gl-matrix库进行矩阵计算,证明了这种方法的有效性。
本文介绍了如何通过矩阵变换将局部坐标系的坐标转换为全局坐标系,反之亦然。首先,通过一个简单的示例解释坐标变换的直观理解,然后详细阐述坐标实际表示坐标轴单位向量的数量。接着,利用node.js编程验证了变换矩阵的正确性,通过构建三维变换矩阵实现一步到位的坐标转换。最后,通过gl-matrix库进行矩阵计算,证明了这种方法的有效性。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








