摘要
多模态图像融合旨在通过整合和区分来自多个源图像的跨模态互补信息生成融合图像。虽然具有全球空间交互的跨注意力机制看起来很有前景,但它仅捕获二阶空间交互,忽略了空间和通道维度的高阶交互。
作者提出了一种协同高阶交互范式(Synergistic High-order Interaction Paradigm,SHIP),旨在系统性地研究多模态图像在两个基本维度上的空间细粒度和全局统计协作:
- 空间维度:作者通过逐元素乘法构建空间细粒度交互,数学上等同于全局交互,然后通过迭代聚合和演变互补信息来促进高阶格式,从而提高效率和灵活性。
- 通道维度:在通道交互的基础上扩展一阶统计(均值),作者设计高阶通道交互,以促进基于全局统计的源图像之间的相互依赖性辨别。
作者进一步引入了SHIP模型的增强版本,称为SHIP++,它通过跨阶注意力演变机制、跨阶信息集成和残差信息记忆机制增强跨模态信息交互表示。
正文
如果只使用单一光学配置或传感器捕获的图像往往无法提供场景的全面或详细表示。通过结合其他的传感器的技术,可以被证明:能有效的捕捉更完整和整体的场景信息。
将红外与可见光图像融合(VIF)目标是将源图像中的互补信息聚合并辨识到融合图像中,从而增强其在后续任务中的适用性。
现在,深度学习在图像融合领域有了巨大的突破,然而现在的神经网络都只局限于空间维度的二阶(如下图所示),忽视了在空间和通道维度中的高阶交互的未开发的潜力。这会导致对协同模态相关性的探索受限。
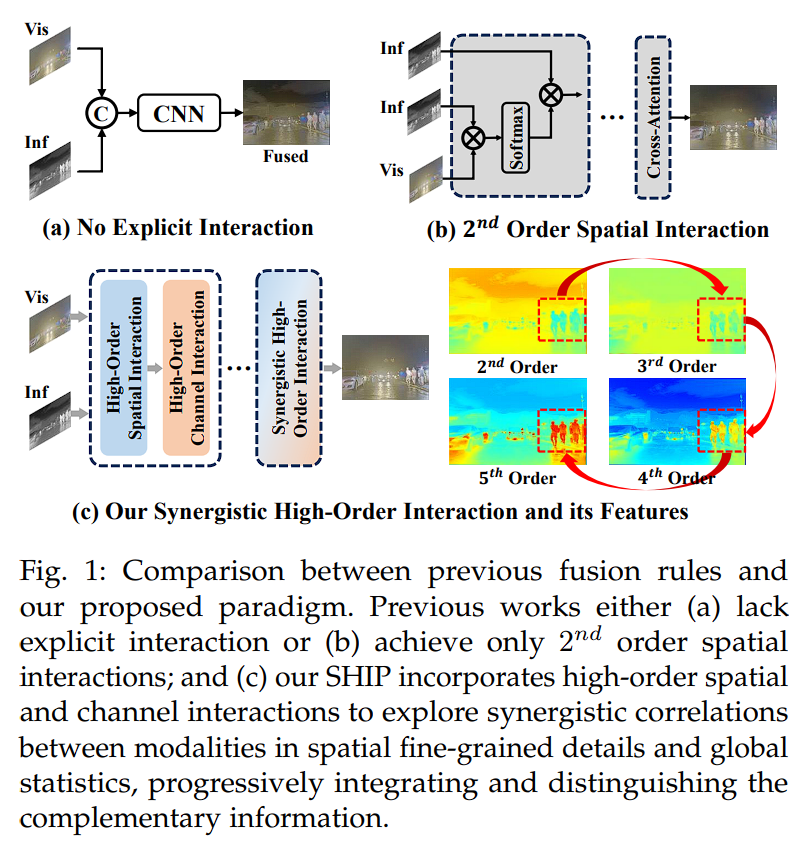
作者的目标是建模空间与通道维度中的高阶交互,从而全面探索模态之间的协同作用。作者引入了一种协同高阶交互范式(Synergistic High-order Interaction Paradigm,SHIP),提供了一种创新的方法,通过高阶交互有效捕捉多模态之间的空间细粒度和全局统计的协同效应。
有两个维度:
- 空间维度:利用频域通过逐元素相乘建立跨模态表示之间的空间细粒度相关性,这是一种数学上等效但计算上高效的替代方案,取代了成本高昂的矩阵乘法。
- 通道维度:基于SE块使用一阶统计量(均值)进行一阶通道交互的自适应重校准特征响应,我们将这一概念提升到高阶格式。这一扩展使得能够探索基于源图像全局统计的协同相关性,从而更深入地洞察不同模态之间复杂的相互依赖关系。
贡献
- 开创了多模态图像融合中高阶交互的探索,通过在空间和通道维度中引入高阶交互,提出了一种新颖的协同高阶交互范式(SHIP)来研究多模态之间协同相关性
- 该范式深入探讨了涉及空间细粒度和全局统计的高阶交互,协同聚合互补信息并区分来自多个源模态的相互依赖关系。
- 通过定量和定性实验,我们证明了所开发的SHIP(++)在多模态图像融合任务中的优越性。
方法
总览
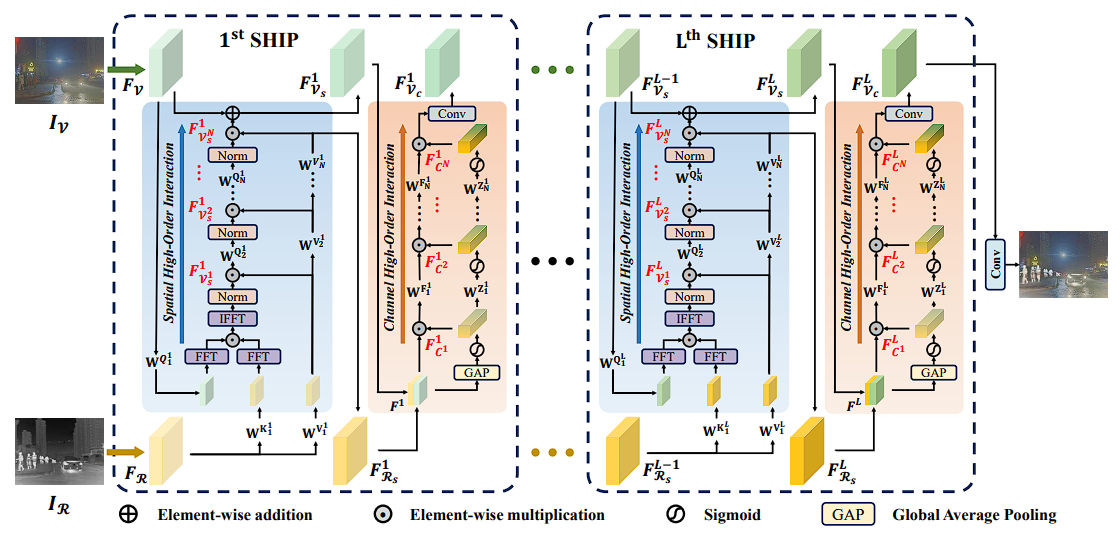
整体的流程如下:给定一个红外图像 I R ∈ R H ∗ W ∗ 1 I_R \in R^{H*W*1} IR∈RH∗W∗1 与一个可见光图像 I V ∈ R H ∗ W ∗ 3 I_V \in R^{H*W*3} IV∈RH∗W∗3,首先使用单独的卷积层为每种模态提取相应的浅层特征,得到 F R ∈ R H ∗ W ∗ C F_R \in R^{H*W*C} FR∈RH∗W∗C 和 F V ∈ R H ∗ W ∗ C F_{V} \in R^{H*W*C} FV∈RH∗W∗C。然后这些模态感知特征经过一系列核心协同高阶交互范式(SHIP),结合了空间和通道维度。这个过程探索了两种模态在空间细粒度和全局统计信息之间的协同作用。最后这些特征被投影回图像空间以生成融合结果。融合过程特别针对YCbCr颜色空间中的Y通道。
这个过程可以被表述为:
I
F
=
S
H
I
P
L
(
ψ
(
I
R
)
,
ϕ
(
I
V
)
)
I_F = SHIP_L(\psi(I_R), \phi(I_V))
IF=SHIPL(ψ(IR),ϕ(IV))
其中
ϕ
\phi
ϕ 与
ψ
\psi
ψ 表示特征提取器,
L
L
L 表示 SHIP 的迭代次数。在全色锐化中,这个范式表示为:
I
F
=
S
H
I
P
L
(
ψ
(
I
P
)
,
ϕ
(
I
M
)
)
+
I
M
I_F = SHIP_L(\psi(I_P), \phi(I_M)) + I_M
IF=SHIPL(ψ(IP),ϕ(IM))+IM
高阶空间交互
输入 F v F_v Fv 为中心的二阶空间交互:
O S ( ( F V ) 2 ) = F V S 1 = softmax ( Q ⊗ K T d k ) ⊗ V = A ⊗ V O_S((F_V)^2) = F^1_{V_S} = \text{softmax} \left( \frac{Q \otimes K^T}{\sqrt{d_k}} \right) \otimes V = A \otimes V OS((FV)2)=FVS1=softmax(dkQ⊗KT)⊗V=A⊗V
由于 transformer 机制中的点积操作是二次时间复杂度,所以这会导致显著的计算开销,所以在级联自注意力机制中进行高阶操作是不可取的。
等效高效形式
如果将 A 的每个元素使用邮件管理员重新定义: A i j = ⟨ q i , k j ⟩ , q i ∈ Q , k j ∈ K A_{ij} = \langle q_i, k_j \rangle, \quad q_i \in Q, \quad k_j \in K Aij=⟨qi,kj⟩,qi∈Q,kj∈K。 ⟨ ⟩ \langle \rangle ⟨⟩ 表示内积。卷积定理指出,空间域中两个信号的相关或卷积赞同于其在频域中的 Hadamard 积。如下所示:
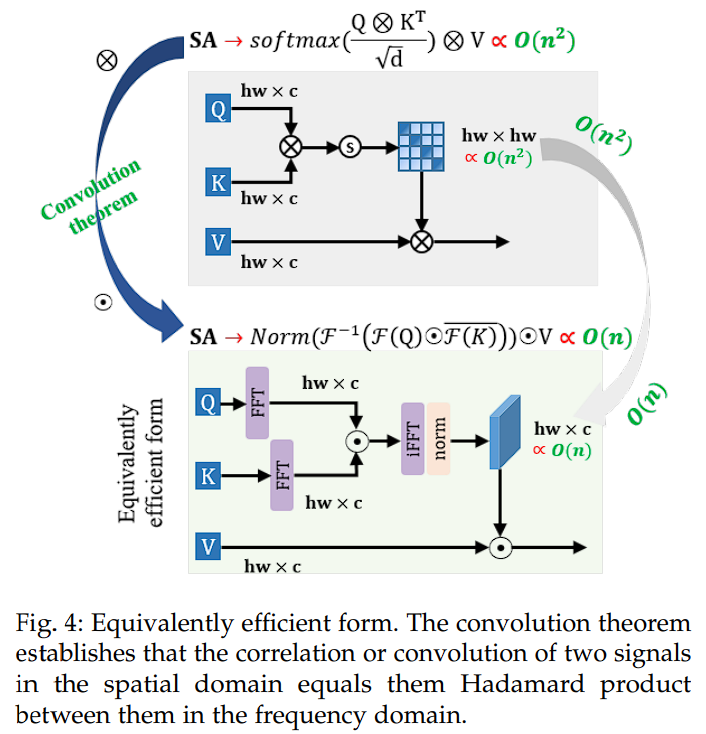
为了利用这一特性,作者将频域整合到自注意力机制中,将矩阵乘法的计算复杂度降低为更高效的逐元素操作。首先,作者使用快速傅里叶变换(FFT)将模态感知特征FRFR和FVFV转换到频域。相关性计算如下:
A
=
F
−
1
(
F
(
F
V
W
Q
)
⊙
F
(
F
R
W
K
)
‾
)
A = F^{-1} \left( F(F_VW_Q) \odot \overline{F(F_RW_K)} \right)
A=F−1(F(FVWQ)⊙F(FRWK))
F
(
)
F()
F() 为 FFT,而
F
−
1
(
)
F^{-1}()
F−1() 为逆 FFT。
⊙
\odot
⊙ 表示 Hadamard 积,
F
(
)
‾
\overline{F()}
F() 表示共轭转置操作。二阶空间交互的集成特征为:(公式 5)
O
S
(
(
F
V
)
2
)
=
F
V
S
1
=
Norm
(
A
)
⊙
(
F
R
W
V
)
O_S((F_V)^2) = F^1_{V_S} = \text{Norm}(A) \odot (F_RW ^V)
OS((FV)2)=FVS1=Norm(A)⊙(FRWV)
深入高阶
形式上,L个级联自注意力的递归格式可以表示为:
O
S
(
(
F
V
S
i
−
1
)
2
)
=
F
V
S
i
=
Attention
(
Q
i
,
K
i
,
V
i
)
,
Q
i
=
F
V
S
i
−
1
W
Q
i
,
K
i
=
F
R
W
K
i
,
Q
i
=
F
R
W
V
i
,
\mathcal{O}_S((F_{V_S}^{i-1})^2) = F_{V_S}^i = \text{Attention}(Q_i, K_i, V_i), Q_i = F_{V_S}^{i-1} \mathbf{W}^{Q_i}, \quad K_i = F_R \mathbf{W}^{K_i}, \quad Q_i = F_R \mathbf{W}^{V_i},
OS((FVSi−1)2)=FVSi=Attention(Qi,Ki,Vi),Qi=FVSi−1WQi,Ki=FRWKi,Qi=FRWVi,
。显然灾个过程仅捕获关于输入特征
F
V
s
i
−
1
F_{V_s}^{i-1}
FVsi−1 的二阶交互,同时引发了巨大的计算成本。
相反,在等效高效形式的基础上,可以超越二阶交互,并在保持效率的同时扩展到任意阶的交互(N 阶)。具体而言,对于每次第 i 次迭代,将公式 5扩展为以下高阶公式:
$$
\mathcal{O}S((F{V}{i-1})j) = F_{V_Sj}i = \text{Norm}(F_{V_S{j-1}}{i} \mathbf{W}^ {\mathbf{Q}j^i}) \odot (F{R_S{j-1}}i \mathbf{W} {\mathbf{V}j}),
F_{V_S{j-1}}{i} = \text{Norm}(F_{V_S{j-2}}{i} \mathbf{W} {\mathbf{Q}_{j-1}i)}, \quad F_{R_S{j-1}}{i} = F_{R_S{j-2}}{i} \mathbf{W} {\mathbf{V}i_{j-1}},
$$
j
∈
[
2
,
N
]
j \in [2,N]
j∈[2,N] 这一个公式可以高效的捕获到 N 阶的交互。
一般来说,对于下图的 transformer 链,序列展开如下:
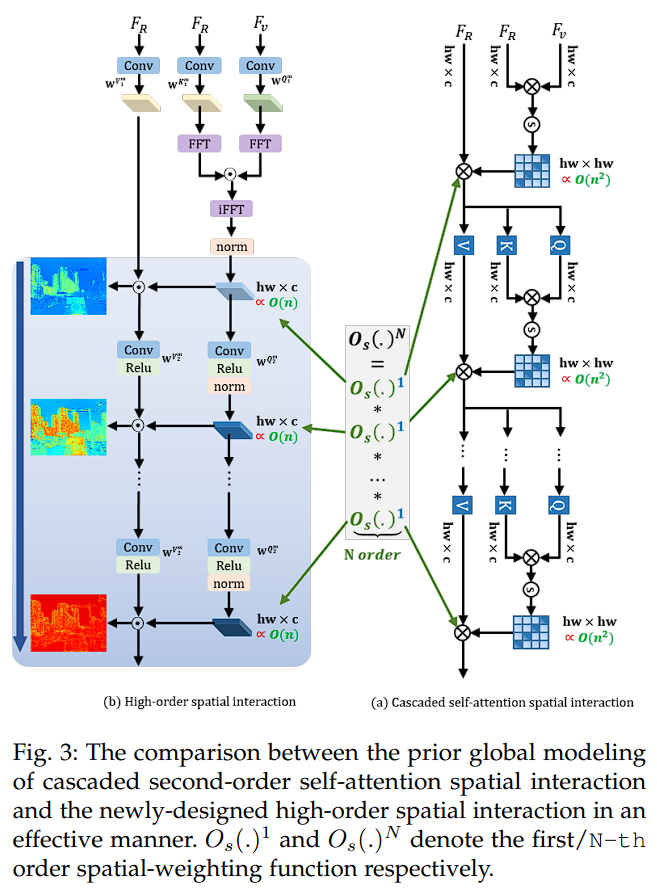
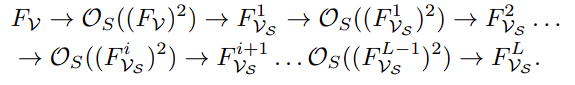
而作者的高阶建模将其替换为:
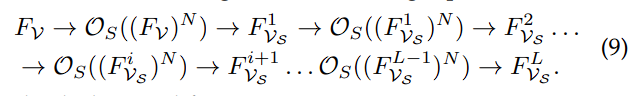
这一修改可以使得作者在每次迭代中捕获到 N 阶的交互。
可以从可视化结果看到:每个空间高阶交互中的不同阶次整合了不同粒度的互补信息。此外,不同迭代中的交互表现出判别性的响应,通过整个迭代过程丰富了特征多样性。
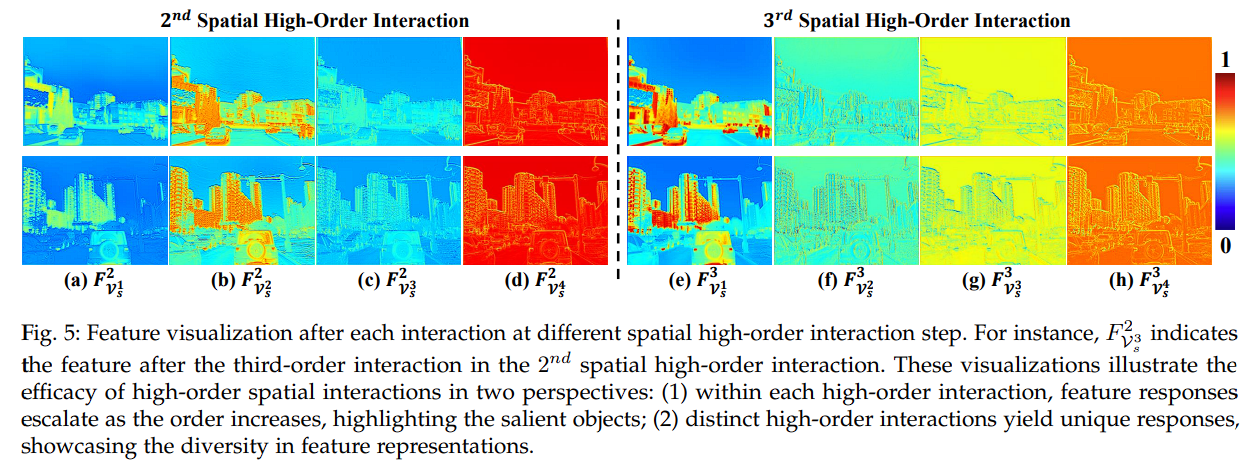
高阶通道交互
SE 模块利用一阶全局统计量(均值)来建模通道交互。这一方法使 SE 块可以显式捕获输入特征通道之间的相互依赖性。对于红外和可见光图像融合,SE 块将红外和可见光特征之间的依赖关系从第 i 次高阶空间交互中定义为:
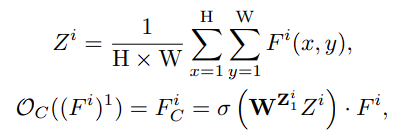
其中, F i = [ F V s i , F R s i ] F^i=[F^i_{V_s}, F^i_{R_s}] Fi=[FVsi,FRsi], Z c Z_c Zc 表示一阶统计量, σ \sigma σ 表示 sigmoid 函数。 W Z W^Z WZ 表示两个线性变换和一个 ReLU 函数。
深入高阶格式
类似于高阶空间交互,作者扩展 Se 块从而实现高阶通道交互:
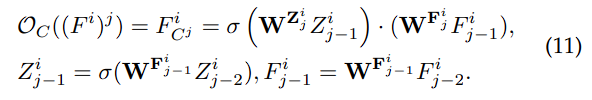
最后一个卷积层将 F C i F^i_C FCi 整合到融合模态中,得到集成特征 F V C i F_{V_C}^i FVCi。
通过 L 次迭代中进行的 N 阶空间和通道交互,交互链可以数学表达如下:
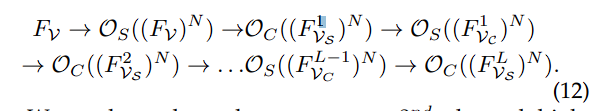
作者分析了第 2 次通道高阶交互中沿通道维度的通道响应。与不同的一致响应相反,作者的高阶建模自适应区分源模态之间的相互依赖性如下所示:
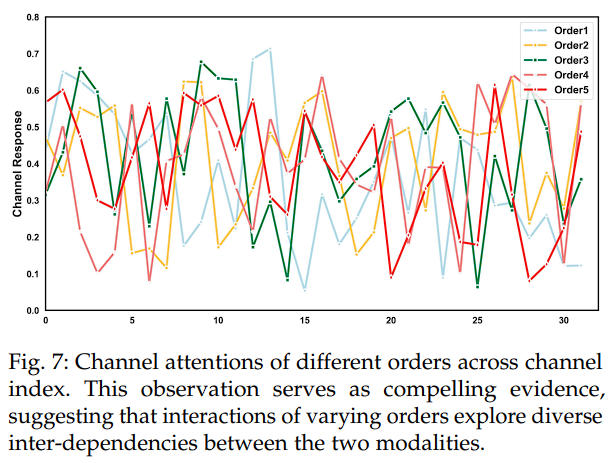
该图片展示了不同序列的通道注意力在各通道索引上的变化。图中有五种不同颜色的线条,分别代表五个不同的序列(Order1 到 Order5)。横轴表示通道索引,纵轴表示通道响应。
基于 SHIP++的重开发组件
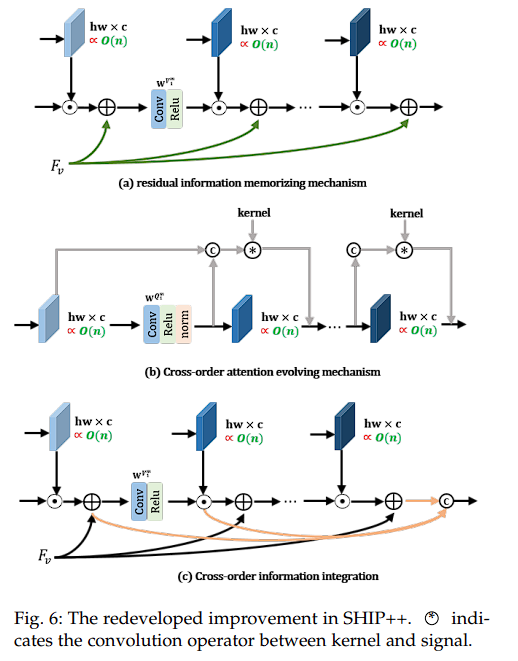
残差信息记忆
由于 VIF 中的可见光图像与图像融合中的低分辨率多光谱图像是主要模态,包含了任务所需的重要的信息。所以在网络学习的过程中保留这些模态的信息很重要,但是在模型的更新过程中,主要模态只参与了最终的学习阶段,这会导致在中间步骤中信息保留不佳。
所以为了保留重要的细节,作者为主要模态实施了残差信息记忆机制,如下图 a 所示:
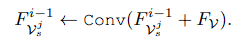
跨顺序信息整合
通过跨顺序方式整合多样信息来跨模态交互的表示,如下图 b 所示。这一改进使我们可以生成更具信息性的表示,利用了不同阶段倾向于捕捉多样化和互补模式的观察结果:

跨阶注意力演化机制
受演化注意力的启发,作者引入了跨阶注意力演化机制,如下图 c 所示。该机制促进了不同层注意力图之间共同知识的共享。因此,早期层的注意力可以通过残差连接指导后续层的注意力,从而能够捕捉精确的模式。
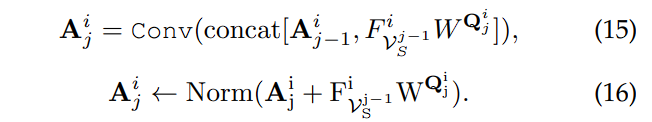
全色锐化的损失函数
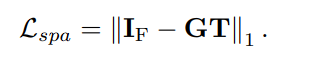
I F I_F IF 和 G T GT GT 表示输出和基准。
VIF 的损失函数
损失函数包括强度和梯度项: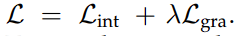 ,其中
λ
\lambda
λ 表示权衡参数。
,其中
λ
\lambda
λ 表示权衡参数。
为了强调可见光和红外图像中的显著对象,作者引入了基于显著性的强度损失,定义如下:
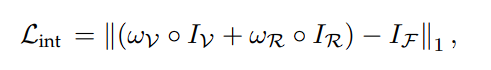
∣
∣
∣
∣
1
|| \ ||_1
∣∣ ∣∣1 表示
L
1
L_1
L1 范数,加权图
ω
v
\omega _v
ωv 和
ω
R
\omega_R
ωR 分别从可见光和红外图像中导出,其中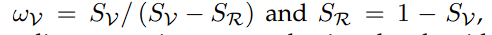 ,S 是使用
,S 是使用
“Saliency guided image detail enhancement,” in 2019 National Conference on Communications (NCC). 这个中的算法计算的显著性矩阵。
L g r a L_{gra} Lgra 对应纹理损失,引导融合图像保留复杂的纹理细节。作者研究表明,捕捉融合图像中最佳纹理的最有效方法涉及红外和可见光图像纹理的最大聚合。因此,我们将纹理损失公式化如下:
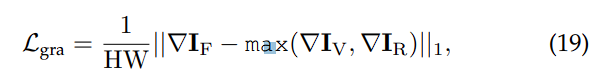
Δ \Delta Δ 表示计算梯度图的操作,量化图像中的纹理信息。这种情况下,使用 sobel 算子进行梯度计算。
基于 VIF 的实验
在三个公开的数据集上进行了实验:M3FD、RoadScene和TNO。
高质量的融合图像应该同时捕捉多模态图像中的显著对象和视觉质量。为全面衡量融合结果,我们采用了七个指标,包括空间频率(SF)、互信息(MI)、视觉信息保真度(VIF)、平均梯度(AG)、SCD、Qabf和特征互信息(FMI)。选择这些指标是因为它们能够评估融合性能的各个方面,通常更高的值表示更好的融合质量。
与最新的方法进行比较
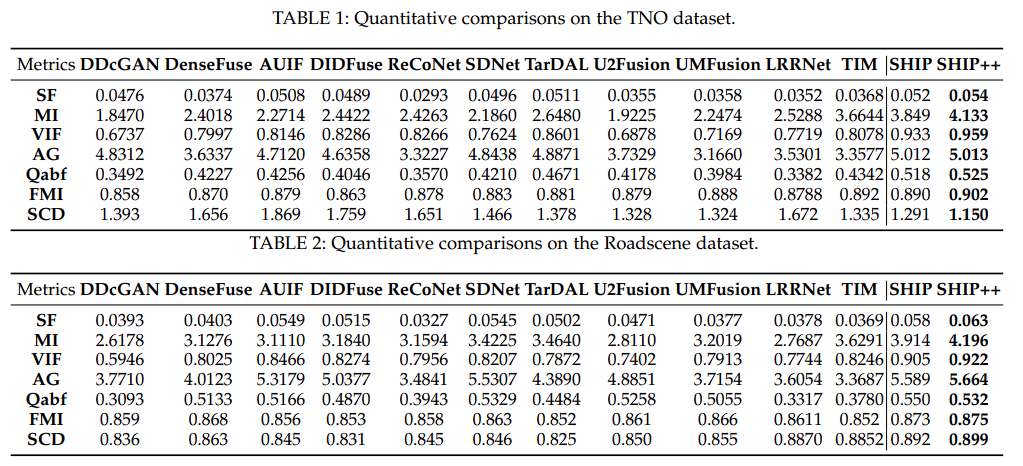
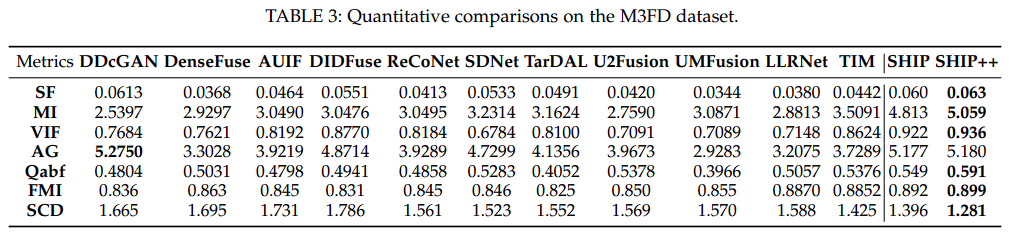
表1、2和3显示了作者的方法在三个数据集上多个指标的卓越表现。较高的MI和FMI分数突出了作者模型利用两个源图像信息的熟练程度,证明了其将丰富数据整合到融合输出中的有效性。此外,在SF、AG、Qabf和SCD方面的优异表现反映了该模型在合并多模态互补信息的同时保留精细纹理细节的卓越能力。这些因素有助于保持精细纹理并产生视觉上引人注目和详细的融合图像。此外,最高的VIF分数强调了我们的融合结果具有高视觉质量和最小失真,符合人类视觉感知。
对于阶数 N 和迭代次数 L 的消融研究
在M3FD数据集上进行消融研究
阶数N 的影响:

上图表示:随着阶段数的,性能显著提高,直到达到 5。之后提升不多。所以作者选择 5 为默认的阶数。
迭代次数 L 的影响:

随着块数的增加,模型性能显著提高。然而,进一步增加L导致SF和AG呈现下降趋势,可能是由于梯度传播面临挑战。因此,我们在所有实验中采用L = 3作为默认块数。
关于空间和通道维度交互的消融研究
对于默认架构,我们首先在空间维度执行N阶交互,然后在通道维度执行:
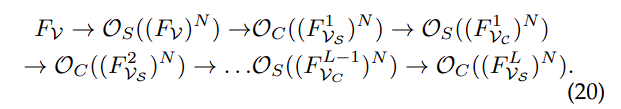
在这项消融研究中,我们交换了两个维度的顺序,先从通道维度开始,然后是空间维度。

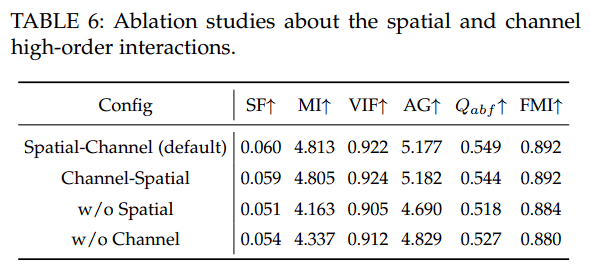
表6和图15中的结果表明,通道和空间维度的顺序对模型性能影响很小,从而验证了我们提出的高阶交互机制的稳健性。
同时,表 6 也可以发现:当删除空间或通道维度时,性能显著下降。因此,空间和通道维度的协同参与对于有效聚合空间细粒度相关性和区分红外和可见光模态之间的全局相互依赖性至关重要。
全色锐化实验
目标是通过与代表性方法进行全面比较,来评估SHIP(++)的有效性。
采用了几个图像质量评估(IQA)指标,包括相对无量纲全局合成误差(ERGAS)、峰值信噪比(PSNR)、结构相似性(SSIM)、相关系数(SCC)、Q值、光谱角度映射器(SAM)、光谱失真指数Dλ、空间失真指数DS以及无参考质量(QNR)。
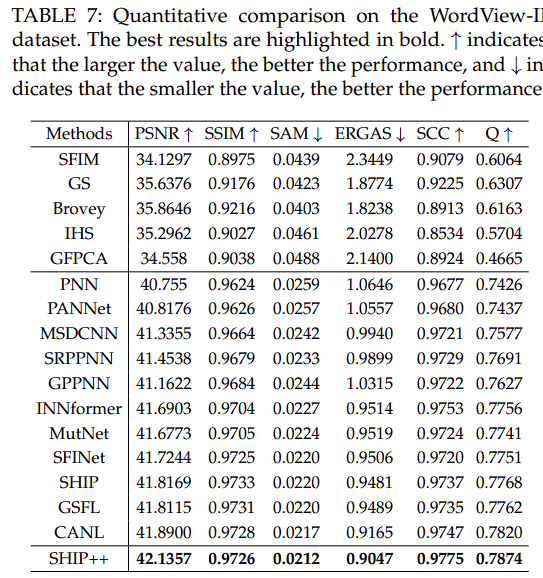
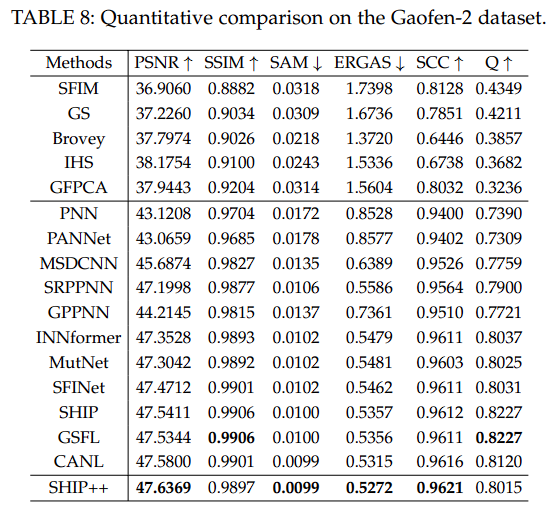
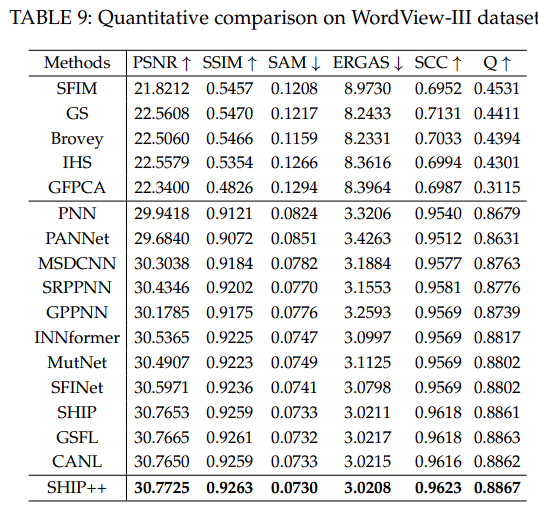
这些表格强调了我们方法的卓越性能,证明它在所有指标上都优于比较算法。
SHIP++的消融实验
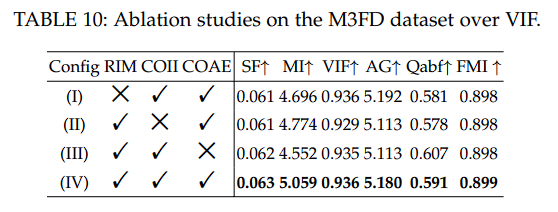
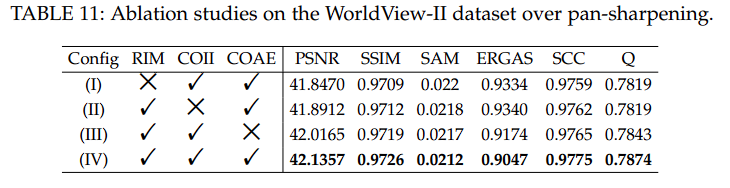
以上两个表表明:残差信息记忆(RIM),跨阶信息集成(COII),跨阶注意力演化机制(COAE) 去除任意一个都会导致性能下降。























 220
220

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








