泰勒级数在语音增强中的应用

扫盲=前言

这些储备知识有的忘记了，有的就没学过，还要从头慢慢来学

泰勒级数

定义

【摘抄百度】泰勒级数是以于1715年发表了泰勒公式的英国数学家布鲁克·泰勒（Sir Brook Taylor）的名字来命名的。通过函数在自变量零点的导数求得的泰勒级数又叫做麦克劳林级数，无限项连加式(级数)来表示一个函数，这些相加的项由函数在某一点的导数求得。说到此其实跟傅里叶级数也有一些相似之处。假设$f(x_0)$在$x_0$附近有任意阶导数，则$f(x_0)$在$x_0$点展开的泰勒级数为$$\sum _{n=0}^{\infty }\frac{f^{(n)}(x_0)}{n!}(x-x_0{)}^n=f(x_0)+f^{\prime }(x_0)(x-x_0)+\frac{f^{\prime \prime }(x_0)}{2!}(x-x_0{)}^2+...+\frac{f^{(n)}(x_0)}{n!}(x-x_0{)}^n+...$$

泰勒级数扩展

根据定义，令$\delta x=x_0-x$，一个函数$f(x)$在某一处$x$位置展开的泰勒形式改写如下：$$f(x+\delta x)=f(x)+f^{\prime }(x)\delta x+\frac{1}{2!}{f}^{\prime \prime }\delta x^2+\frac{1}{3!}{f}^{\prime \prime \prime }\delta x^3+...$$如果$\delta x$非常小，高阶项可以忽略，用二阶截止展开开近似：
$$f(x+\delta x)\approx f(x)+f^{\prime }(x)\delta x+\frac{1}{2!}{f}^{\prime \prime }\delta x^2$$在工程误差允许的范围，甚至直接用一阶线性展开$$f(\mathbf{x}+\delta \mathbf{x})\approx f(\mathbf{x})+f^{\prime }(x)\delta x$$

多变量泰勒级数

对于多变量函数$f(\mathbf{x})=f(x_1,...,x_N)$，同样被展开为泰勒级数，工程中一般用到二阶展开较多：
$$f(x+\delta x)\approx f(x)+\sum _{j=1}^N\frac{\partial f(\mathbf{x})}{\partial x_j}\delta x_j+\frac{1}{2!}\sum _{i=1}^N\sum _{j=1}^N\frac{{\partial }^{2}f(\mathbf{x})}{\partial x_i\partial x_j}\delta x_i\delta x_j$$
假设$\delta \mathbf{x}=[\delta x_1,...,\delta x_N{]}^T$，并令$\mathbf{g}$作为梯度向量$\mathbf{g}={\mathbf{g}}_f(\mathbf{x})=▽f(\mathbf{x})=[\frac{\partial f(\mathbf{x})}{\partial x_1},...,\frac{\partial f(\mathbf{x})}{\partial x_N}{]}^T$，令$\mathbf{H}$表示为黑塞矩阵（多元函数的二阶偏导数构成的方阵）$$\mathbf{H}={\mathbf{H}}_f(x)=\frac{d}{d\mathbf{x}}{\mathbf{g}}_f(\mathbf{x})=\left[\begin{array}{ccc}\frac{{\partial }^{2}f(\mathbf{x})}{\partial x_1^2}& \cdots & \frac{{\partial }^{2}f(\mathbf{x})}{\partial x_1\partial x_N}\\ ⋮& \ddots & ⋮\\ \frac{{\partial }^{2}f(\mathbf{x})}{\partial x_N\partial x_1}& \cdots & \frac{{\partial }^{2}f(\mathbf{x})}{\partial x_N^2}\end{array}\right]$$

用向量和矩阵来表达
$$f(\mathbf{x}+\delta \mathbf{x})\approx f(x)+{\mathbf{g}}^T\delta \mathbf{x}+\frac{1}{2!}{\mathbf{x}}^T\mathbf{H}\delta \mathbf{x}$$

多变量矢量函数的泰勒展开

在多变量的基础上，一组函数的向量表达如下：$$\mathbf{f}(\mathbf{x})=[f_1(\mathbf{x}),...,f_M(\mathbf{x}){]}^T$$
联系上节内容，某一项的展开为$$f_i(x+\delta x)\approx f_i(x)+{\mathbf{g}}_i^T\delta \mathbf{x}+\frac{1}{2!}{\mathbf{x}}^T{\mathbf{H}}_i\delta \mathbf{x}$$
但是矢量合成的二维展开的二阶项是一个张量（三维），太烧脑，所以一般只保留一阶项展开$$\mathbf{f}(\mathbf{x}+\delta \mathbf{x})\approx \mathbf{f}(\mathbf{x})+{\mathbf{J}}_f(\mathbf{x})\delta \mathbf{x}$$
这里${\mathbf{J}}_f(\mathbf{x})$即向量函数$\mathbf{f}(\mathbf{x})$的雅可比矩阵（）：
$$\begin{gathered} {\mathbf{J}}_f(\mathbf{x})=\frac{d}{d\mathbf{x}}=\left[\begin{array}{c}{f}_1\\ ⋮\\ f_M\end{array}\right][\frac{\partial }{\partial x_1}...\frac{\partial }{\partial x_N}] \\ =\left[\begin{array}{ccc}\frac{\partial f_1}{\partial x_1}& \cdots & \frac{\partial f_1}{\partial x_N}\\ ⋮& \ddots & ⋮\\ \frac{\partial f_M}{\partial x_1}& \cdots & \frac{\partial f_M}{\partial x_N}\end{array}\right] \end{gathered}$$

应用方向

以下是总知网看到的一个介绍【2】，差不多概括了vts在降噪领域的一个应用方向

矢量泰勒级数是一种有效的抗噪声鲁棒语音识别算法.虽然在对数谱域,美尔滤波器组的不同通道之
间有较强的相关性,因而难以从含噪语音中准确估计噪声的方差.但是基于矢量泰勒级数的倒谱域特
征补偿算法,用一个高斯混合模型描述语音倒谱特征的分布,通过矢量泰勒级数从含噪语音中估计噪
声的均值和方差.能明显提高语音识别系统的性能.

那么如何应用，有何好处呢，说来话长了。

VTS在变换域的鲁棒性应用

追溯VTS最早的文章是1996年的《A vector Taylor series approach for environmentindependent speech recognition》，是CMU大学做语音识别的一遍论文，联系到当时GMM-HMM的主流模型，这篇文章也是在此框架下的一个改进。改论文不仅建模了VTS分析方法，还提出了应用的两个方向：

1. 直接对语音进行补偿（语音增强），然后识别
2. 利用VTS的公式改进HMM统计模型。
   上述两个方法仅仅需要的是待识别的受噪声污染的语音片段，通过VTS模型来实现环境鲁棒性的补偿。不仅如此，论文还强调了改方法针对各种统计模型都是有效果的，利用统一的方法就可以实现噪声和信道的重估计。

环境建模

典型的环境噪声是加性和卷积混叠的，为了分析方便往往认为卷积和加性是串联的，如下图【4】：

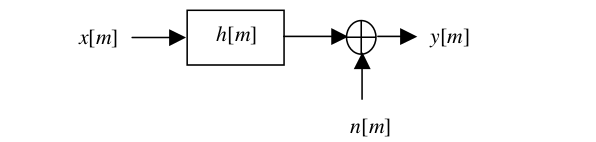
由此对于数字序列来说，得到如下IPO公式：
$$y(m)=x(m)\ast h(m)+n(m)$$变换到频域的功率（幅度平方）表征： ∣ Y ( f k ) ∣ 2 = ∣ X ( f k ) ∣ 2 ∣ H ( f k ) ∣ 2 + ∣ N ( f k ) ∣ 2 + 2 R e { X ( f k ) H ( f k ) N ∗ ( f k ) } |Y(f_k)|^2=|X(f_k)|^2|H(f_k)|^2+|N(f_k)|^2+2Re\{X(f_k)H(f_k)N^*(f_k)\} ∣Y(fk​)∣2=∣X(fk​)∣2∣H(fk​)∣2+∣N(fk​)∣2+2Re{X(fk​)H(fk​)N∗(fk​)}
上面这个公式还是容易理解的，但不容易操作，所以假设x(m)和n(m)是统计独立的，最后一项的 期望就是零均值，而经过试验也能证明这一项的误差是可以接受的，所以就大胆的省掉难看的尾项$$|Y(f_k){|}^2=|X(f_k){|}^2|H(f_k){|}^2+|N(f_k){|}^2$$换到对数谱领域，$Y_{ln}=ln(|Y(f_k){|}^2)=>|Y(f_k){|}^2=exp(Y_{ln})$进行带入：$$ln(exp(Y_{ln}))=ln(exp(X_{ln}{H}_{ln})+exp(N_{ln}))=ln(exp(X_{ln}{H}_{ln}))+ln(1+\frac{exp(N_{ln})}{exp(X_{ln}{H}_{ln})})$$经过代数运算得出如下的通用形式，在【4】中给的推导结果如下：
$$ln|Y(f_k){|}^2=ln|X(f_k){|}^2+ln|H(f_k){|}^2+ln(1+exp(|N(f_k){|}^2-ln|X(f_k){|}^2-ln|H(f_k){|}^2))$$这样就可以概括为一个更加通用的表达：$$z=x+f(x,n,h)$$此处的h参数无法估计，它表达的是在对数频谱（能量谱）域线性滤波的影响【1】。那么VTS算法关键就是拟合这个通用表达。$$\begin{gathered} f(x,n,h)\approx f(x_0,n_0,h_0)+\frac{d}{dx}f(x_0,n_0,h_0)(x-x_0)+ \\ \frac{d}{dn}f(x_0,n_0,h_0)(n-n_0)+\frac{d}{dh}f(x_0,n_0,h_0)(h-h_0)+... \end{gathered}$$
在【1】中，作者强调了虽然泰勒（截断）扩展普适性很强，但是如果$x$符合高斯分布，那么围绕均值的扩展将更加具有魅力，所以就可以放心大胆的用截断表达来替换原来复杂的函数，一般用到一阶就够了。

与高斯模型方法的结合

【1】干净语音的统计方法即通过EM算法进行GMM建模，是经典ASR算法的基础。VTS方法试图通过纯净语音的pdf，带噪声音片段和泰勒级数建模纯净和带噪语音的关系，来估计带噪语音的pdf。而一旦带噪语音的pdf参数确定了，就可以利用MMSE方法来预测（不可观测）的干净语音序列。这篇文章还提到了如果利用HMM进行纯净语音的pdf训练，那么泰勒级数就用来估计受噪语音的HMM，从而实现路鲁棒性的语音识别，但没有展开。而针对于降噪方面，假设纯净语音是高斯的，那么VTS扩展同样是高斯的，受噪语音的pdf表示为$p(z)={\mathcal{N}}_z({\mu }_z,{\Sigma }_z)$，这时零阶（VTS-0）扩展表示$$\begin{array}{rl}{\mu }_z& =E(z)=E(x+f(n_0,x_0,h_0))={\mu }_x+f(n_0,x_0,h_0)\\ {\Sigma }_z& ={\Sigma }_x\end{array}$$一阶（VTS-1）扩展表示$$\begin{array}{rl}{\mu }_z=& E(x+f(n_0,x_0,h_0))={\mu }_x+f(n_0,x_0,h_0)+\\ & E(\frac{d}{dx}f(x_0,n_0,h_0)(x-x_0))+\\ & E(\frac{d}{dn}f(x_0,n_0,h_0)(n-n_0))+\\ & E(\frac{d}{dh}f(x_0,n_0,h_0)(h-h_0))\\ {\Sigma }_z=& (I+\frac{d}{dx}f(x_0,n_0,h_0){)}^T{\Sigma }_x(I+\frac{d}{dx}f(x_0,n_0,h_0))+\\ & (I+\frac{d}{dn}f(x_0,n_0,h_0){)}^T{\Sigma }_n(I+\frac{d}{dn}f(x_0,n_0,h_0))\end{array}$$通过改进的EM算法，就可以估算出带噪的pdf。

利用MMSE方法补偿受噪话音

受噪话音的分布一旦求得，利用下面的公式进行MMSE的纯净语音 估计$${\hat{x}}_{MMSE}=E(x|z)=\int xp(x|z)dx=\int (z-f(x,n,h))p(x|z)dx$$零阶下的估计范式为$${\hat{x}}_{MMSE}=z-\sum _{k=0}^{M-1}f({\mu }_{x,k},{\mu }_n,h)p(k|z)$$但要记住这个估计值是在对数功率谱范式下求得，如果直接进行识别可能最好，但要恢复语音还要进行逆变换。

基于统计模型的梅尔谱维纳滤波

回顾一下加性噪声环境能量谱的公式$$|Y(f_k){|}^2=|X(f_k){|}^2+|N(f_k){|}^2$$
基于此公式的维纳滤波器$G=\frac{|X(f_k){|}^2}{|Y(f_k){|}^2}=\frac{|X(f_k){|}^2}{|X(f_k){|}^2+|N(f_k){|}^2}$。首先论文【6】提出了梅尔谱（对数能量谱）的维纳表达$$G_{t,l}=exp(S_{t,l})/exp(O_{t,l})\approx \frac{exp(S_{t,l})}{exp(S_{t,l})+exp(N_{t,l})}$$
这个增益是作用在梅尔滤波器bin上的。但是实际上纯净的对数梅尔谱$S_{t,l}$是无法求的,所以利用统计模型求出纯净语音的均值方差，利用${\mu }_{S_{t,k,l}}$来替换$S_{t,l}$，$N_{t,l}$也可以估计出来，这样就能够得到基于统计模型的梅尔谱维纳滤波增益函数$${\hat{G}}_{t,k,l}=exp({\mu }_{S_{t,k,l}})/exp({\mu }_{O_{t,k,l}})$$后验概率$p(k|O_t)$加持下，可以得到估算的增益：
$${\hat{G}}_{t,l}=\sum _{k=1}^{K}p(k|O_t){\hat{G}}_{t,k,l}$$
一个简单条件概率公式表达【6】：$$p(k|O_t)=\frac{\mathcal{N}(O_t;{\mu }_{o_{t,k}},{\Sigma }_{o_{t,k}})}{{\sum }_{i=1}^K\mathcal{N}(O_t;{\mu }_{o_{t,i}},{\Sigma }_{o_{t,i}})}$$

参考文档

1. A vector Taylor series approach for environmentindependent
speech recognition, P. J. Moreno, et al.,
2.基于矢量泰勒级数的鲁棒语音识别
3.Taylor series expansion
4.HMM ADAPTATION USING VECTOR TAYLOR SERIES FOR NOISY SPEECH RECOGNITION, Alex Acero, Li Deng… Microsoft Reseach
[5.Model-based compensation of the additive noise for continuous speechrecognition. Experiments using the AURORA II database and tasks]
[6.A study of mutual front-end processing method based on
statistical model for noise robust speech recognition]