2-7、规划问题的Lingo解法

最新推荐文章于 2024-08-16 18:02:52 发布

金陵鸭王

最新推荐文章于 2024-08-16 18:02:52 发布

阅读量7.3k

点赞数 4

分类专栏：数学建模之程序员进阶文章标签：规划问题 lingo 线性规划非线性规划

本文链接：https://blog.csdn.net/gregoryhanson/article/details/79636927

版权

数学建模之程序员进阶专栏收录该内容

16 篇文章 2 订阅

订阅专栏

一、从规划问题引入

在我们学习探索的各个领域，规划问题都是无处不在的。通过列出约束条件及目标函数，再画出约束条件所表示的可行域，就能在可行域内求得目标函数的最优解以及最优值。当然我们在高中就已经学习过线性规划的相关知识，对于理科同学来说，大多数同学应该感觉难度不大，或者说是送分考点。然而到了大学阶段，一些规划问题的求解已经不是人力可以轻松算出来的了，必须借助于计算机来进行计算。那么对于规划问题的软件选择，又应当如何进行呢？

二、软件分析与选择

Matlab相比之下是一个面面俱到的编程软件，也可用于求解规划问题。但是如果一定要去和某些“针对特定功能而开发的软件”去比的话，Matlab有时也会稍显逊色。就好比一款顶级的耳机能通吃高中低音，但是去和另一款顶级的为高音而设计的耳机去比较的话，也难免会被比下去。这也就是为什么在规划问题上，很多人会去使用Lingo进行求解。

首先我们来区分一下Lindo和Lingo这两款软件。Lingo是在Lindo基础之上做成的软件，处理解线性规划问题之外还加了非线性的求解器，更关键的是还追加了集的概念。可以更方便的解决复杂的问题。所以本文只对Lingo进行讲解。
而对于Matlab与Lingo的区别，就好比手动挡与自动挡的区别，有针对性的专业软件会对用户做很多的优化。这里引用知乎上大佬花开花落的回答
https://www.zhihu.com/question/49319704/answer/165923451

用MATLAB求解线性规划和整数规划问题，需要先将问题转化成如下标准型，其中X只能是向量，也就是单下标变量，然后用向量和矩阵来表达目标函数和约束条件。
然而，许多问题（如指派问题和运输问题）由于参数和决策变量是双下标变量，必须在基本的数学模型的基础上进行变换才能求解，这样得到的等式约束和不等式约束的系数矩阵规模就非常庞大，当然由MATLAB计算问题不大，但转换工作完全要由人工完成，工作量大而且容易出错，因此在这一块效率不高。
而LINGO有自己的建模语言，在建立了集合的基础上，能够高效表达目标函数和各种约束条件。所写的模型基本上可以看作是对数学模型的翻译，不需要太多的转换。

那么现在我们基本上对LINGO和MATLAB对规划问题的处理方面有了初步认识与了解，至于是执着于MATLAB还是选择开辟LINGO这片新的领域，取决于队伍自身了。

三、如何上手Lingo

有很多人对于Lingo的评价都是，非常简单的软件，很好上手。
“简单”一词我觉得还比较恰当。Lingo的各种版本几乎全部都是免安装版本的，界面很简单，功能用法很简单，处理问题的方式简单快捷。确实是跟“简单”一词挂钩的。但是任何一款软件想要精通，都是有一定难度的。如果你只需要用Lingo处理一些简单的线性问题，那么2个小时不到，0编程基础的朋友就能上手。如果你认准了Lingo就是你处理各类规划问题的御用软件，那么还是有很长一段路要走的。当然这也取决于用户的编程基础。如果学习过面向对象的程序设计课程的朋友，对于类与对象概念有所了解，那么对于集这一概念也能快速理解上手，学习起来更加轻松。

四、 Lingo的基本语法规则

1、求目标函数的最大最小值用 $MAX=$ 和 $MIN=$ 来表示；
2、每个语句必须用分号“；”结束，每行可以有许多语句，一个语句可以跨行；
3、变量名必须以字母A-Z开头，由字母、数字0-9和下划线组成，长度不超过32个字符，不区分大小写；
4、可以给语句加上标号；
5、注释以“！”开头以“；”结束；
6、默认所有的决策变量为非负数；
7、Lingo模型以“MODEL”开头以“END”结束。
8、Lingo把相联系的对象聚合成集，借助集，就能够用一个单一的长的简明的公式表示一系列相应的约束。
9、Lingo程序会包含集合段，数据输入段，优化目标和约束段，初始段和数据预处理部分。
10、Lingo函数包括有数学函数，金融函数，概率函数，变量界定义函数，集操作函数，集循环函数，输入输出函数，辅助函数等等。

五、谈一谈例子

那么Lingo用起来到底有多简单呢，我们来看一个例子。

例1:某家公诉制造书桌、餐桌和椅子，所用的资源有三种:木料、木工和漆工。生产数据如下表所示:

	每个书桌	每个餐桌	每个椅子	现有资源总数
木料	8个单位	6个单位	1个单位	48个单位
漆工	4个单位	2个单位	1.5个单位	20个单位
木工	2个单位	1.5个单位	0.5个单位	8个单位
成品单价	60个单位	30个单位	20个单位

若要求桌子的生产量不超过5件，如何安排三种产品的生产可使利润最大？

解：代码

max = 60 * desks + 30 * tables + 20 * chairs;
      8 * desks + 6 * tables + chairs <= 48;
      4 * desks + 2 * tables + 1.5 * chairs <= 20;
      2 * desks + 1.5 * tables + .5 * chairs <= 8;
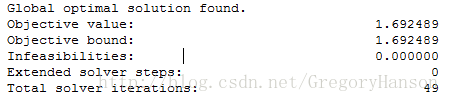
tables <= 5;

可以得到结果:

这里的 Total solver iteration 表示一共迭代2次得到最优解。
Objective value 表示最优值为280，而取280的时候各个变量取多少呢，底下的表格给出了答案。
可以看到，没有定义变量，简简单单一个函数一个约束条件，迅速计算出了答案。Lingo看上去就像是为了非编程人员量身定制的一样。

例2:给定一个直角三角形，求包含该三角形的最小正方形。

我们可以作出如下正方形:

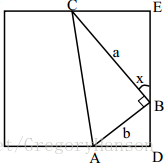
CE=asinx,AD=bcosx,DE=acosx+bsinx C E = a s i n x , A D = b c o s x , D E = a c o s x + b s i n x $CE = asinx, AD = bcosx, DE = acosx + bsinx$

转化为了规划问题那么正方形面积最小的时候即为最优解。
代码：

model:
sets:
    object/1..3/:f;
endsets
data:
    a, b = 3, 4;
enddata
    f(1) = a * @sin(x);
    f(2) = b * @cos(x);
    f(3) = a * @cos(x) + b * @sin(x);
    min = @smax(f(1), f(2), f(3));
    @bnd(0, x, 1.57);
end

得到结果：

这里需要注意，lingo中如果没有代码说明，是默认

x x $x$ 的值大于0的。代码中用

b n d

$bnd$ 函数限制了

x x $x$ 的范围。

那么再进阶一下，Lingo在处理TSP问题的时候表现如何呢？

例3: 现需在一台机器上加工 $n$ 个零件（如烧瓷器），这些零件可按任意先后顺序在机器上加工。我们希望加工完成所有零件的总时间尽可能少。由于加工工艺的要求，加工零件 $j$ 时机器必须处于相应状态 $s_j$ （如炉温）。设起始未加工任何零件时机器处于状态 $s_0$ ，且当所有零件加工完成后需恢复到 $s_0$ 状态。已知从状态 $s_i$ 调整到状态 $s_j ( j ≠ i)$ 需要时间 $c_{ij}$ 零件 $j$ 本身加工时间为 $p_j$ 。为方便起见,引入一个虚零件 $0$ ，其加工时间为 $0$ ，要求状态为 $s_0$ ，则 ${0,1,2,…,n}$ 的一个圈置换 $π$ 就表示对所有零件的一个加工顺序，在此置换下，完成所有加工所需要的总时间为

\sum_{i = 0}^{n} (c_{i π (i)} + p_{i π (i)}) = \sum_{i = 0}^{n} c_{i π (i)} + \sum_{j = 0}^{n} p_{j}

$\sum_{i=0}^n(c_{i\pi (i)}+p_{i\pi(i)})=\sum_{i=0}^nc_{i\pi (i)}+\sum_{j=0}^np_{j}$

由于 $\sum_{j=0}^np_{j}$ 是一个常数，故该零件的加工顺序问题变成TSP。

代码：

!旅行商问题;
model:
sets:
    city / 1.. 5/: u;
    link(city, city):
        dist, x; !距离矩阵;
endsets
    n = @size(city);
data: !距离矩阵，它并不需要是对称的;
    dist = @qrand(1); !随机产生，这里可改为你要解决的问题的数据;
enddata
    min = @sum(link:dist * x);
    @FOR(city(K):
        @sum(city(I)|I #ne# K: x(I, K)) = 1;
        !进入城市K;
        @sum(city(J)|J #ne# K: x(K, J)) = 1;
    );
    @for(city(I)|I #gt# 1:
        @for(city( J)| J#gt#1 #and# I #ne# J:
             u(I) - u(J) + n * x(I,J) <= n - 1);
    );
@for(city(I)|I #gt# 1: u(I) <= n - 2);
@for(link: @bin(x));
end