概率论考点之分布律（重要离散型三大分布）

如题：2019年10月

分析：何为分布律？？由古典概型，可以研究的主要还是概率的概念，得出一系列的单个事件发生的概率问题，主要还是研究AUB的问题。

由条件概率的定义，可以得到全概率与贝叶斯公式，开始研究AB同时发生的问题。

概率论的重要思想就是"由看似不确定的转化为确定的过程".怎么转化?还是离不开抽象与分解.这其实是一个认知的过程,将不认知的东西转化为已知的东西.

要知道分布律,先得知道分布函数的概念:分布函数其实就是说"X<=某个值的概率"这里的概率是不用求的,脑补出这样的图:X称为随机变量.

不需要求概率,这样做的意义是什么?其实就是数学表示元素.没有这个元素,就很难建立起概率论数学抽象.

分布律就是建立在分布函数这个概念基础之上的.就是在分布函数下面加了表示的概率值形成一个图表:主要是针对离散型随机变量.

求P{X<=x}的概率,其实就是这个值之前的概率相加.这些都可以由分布函数的定义可以得出来.

答案就是0.2+0.3=0.5

扩展:这里有好几个分布,一时还真分不太清楚.重要的离散型随机变量的分布就三种，0~1分布，二项分布，泊松分布

0~1分布：只有两种结果

 

二项分布:

注：p+q=1,不是只有0~1分布所特有的，整个二项分布都具有这个性质

不同于几何分布描述的运行到第几次才成功，二项分布描述是的N次试验里有多少次成功。具体如下：

令一组伯努利试验的成功概率为p,失败概率为1-p,则n次伯努利试验中会有多少次成功？

其实就是n重伯努力实验公式.简记为:x ~B(n,p)

 二项式分布特性图:也是0~1分布的形式   X (随机变量）  p(概率），列表就行了。

 

泊松分布:

1、什么是泊松分布？？？

虽然在《再次复习概率论与数理统计之要点总结之前两章》做了一些总结，但还是没有理解，书中其实说的很明白。其实是由泊松定理给出的。

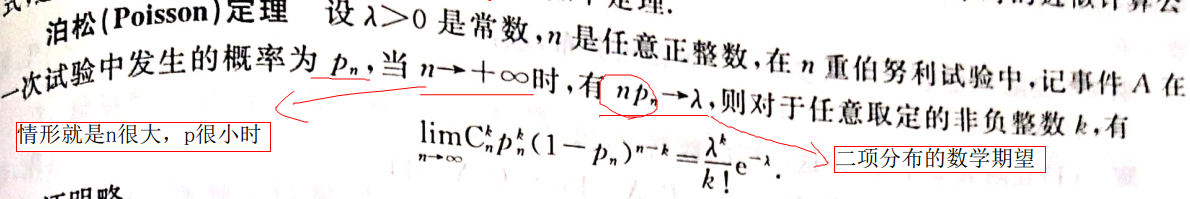
当n很大时，用二项分布的数学期望来代替n,所以泊松分布里没有n,

泊松分布标准定义为：

2、泊松分布的实际意义？？？

由上面的泊松分布的标准定义，可以看到P(x=k),这个k实际是代表了  “发生的次数”，这其实是反向思维，如果已知泊松分布的概率，那么这个次数，就代表连续的时间内，固定发生的次数。

• 某医院平均每小时出生3个婴儿
• 某公司平均每10分钟接到1个电话
• 某超市平均每天销售4包xx牌奶粉
• 某网站平均每分钟有2次访问

它们的特点就是，我们可以预估这些事件的总数，但是没法知道具体的发生时间。已知平均每小时出生3个婴儿，请问下一个小时，会出生几个？

泊松分布就是描述某段时间内，事件具体的发生概率。

上面就是泊松分布的公式。等号的左边，P 表示概率，N表示某种函数关系，t 表示时间，n 表示数量，1小时内出生3个婴儿的概率，就表示为 P(N(1) = 3) 。等号的右边，λ 表示事件的频率。

接下来两个小时，一个婴儿都不出生的概率是0.25%，基本不可能发生。

 接下来一个小时，至少出生两个婴儿的概率是80%。

 泊松分布的图形大概是下面的样子:

可以看到，在频率附近，事件的发生概率最高，然后向两边对称下降，即变得越大和越小都不太可能。每小时出生3个婴儿，这是最可能的结果，出生得越多或越少，就越不可能。 

 

几何分布定义:

在伯努利试验中，记每次试验中事件A发生的概率为p，试验进行到事件A出现时停止，此时所进行的试验次数为X，其分布列为：

此分布列是几何数列的一般项，因此称X服从几何分布，记为X ～ GE(p) 。

实际中有不少随机变量服从几何分布，譬如，某产品的不合格率为0.05，则首次查到不合格品的检查次数X ～ GE(0.05)

如下几何概率分布图: