共形几何2 fundamental Group and Covering Space

monius band 魔比斯环

区分下面两个surface

人可以很轻松的进行区分，一个包括了孔洞环面

对于生活在二维曲面表面的蚂蚁是无法区分的，如果感受内应还是外应关系

内应，本身的性质，还是曲面和R3之间的相对关系

对于蚂蚁是无法跳到三维空间观察孔洞。

在曲面上画圈，有些环线可以通过渐变变为一个点。如果是小猫，就会出现无法缩成点，这个不需要R3信息，只需要surface本身的信息。

对于所有可定向的，紧凑的曲面，可以通过他们的亏格和边界数目进行分类。亏格就是有多少个环柄。对于曲面拓扑，可定向性，亏格数目，边界数目。

下面看一个环柄数目以及方向的例子

如图所示。给定一个封闭曲面，封闭曲面把三维空间分成两部分，一部分是外部一部分是内部。每个环柄上有两个圈，一个红色圈一个绿色圈。红色的圈在外部可以缩成一个点。在内部没办法缩成一个点。绿色的圈刚刚好相反，在内部可以缩成一个点，在外部无法缩成一个点。红圈称为隧道圈，tunnel loop，绿圈称为环柄圈，handle loop。计算部署的话，第一个任务是找到这些圈，

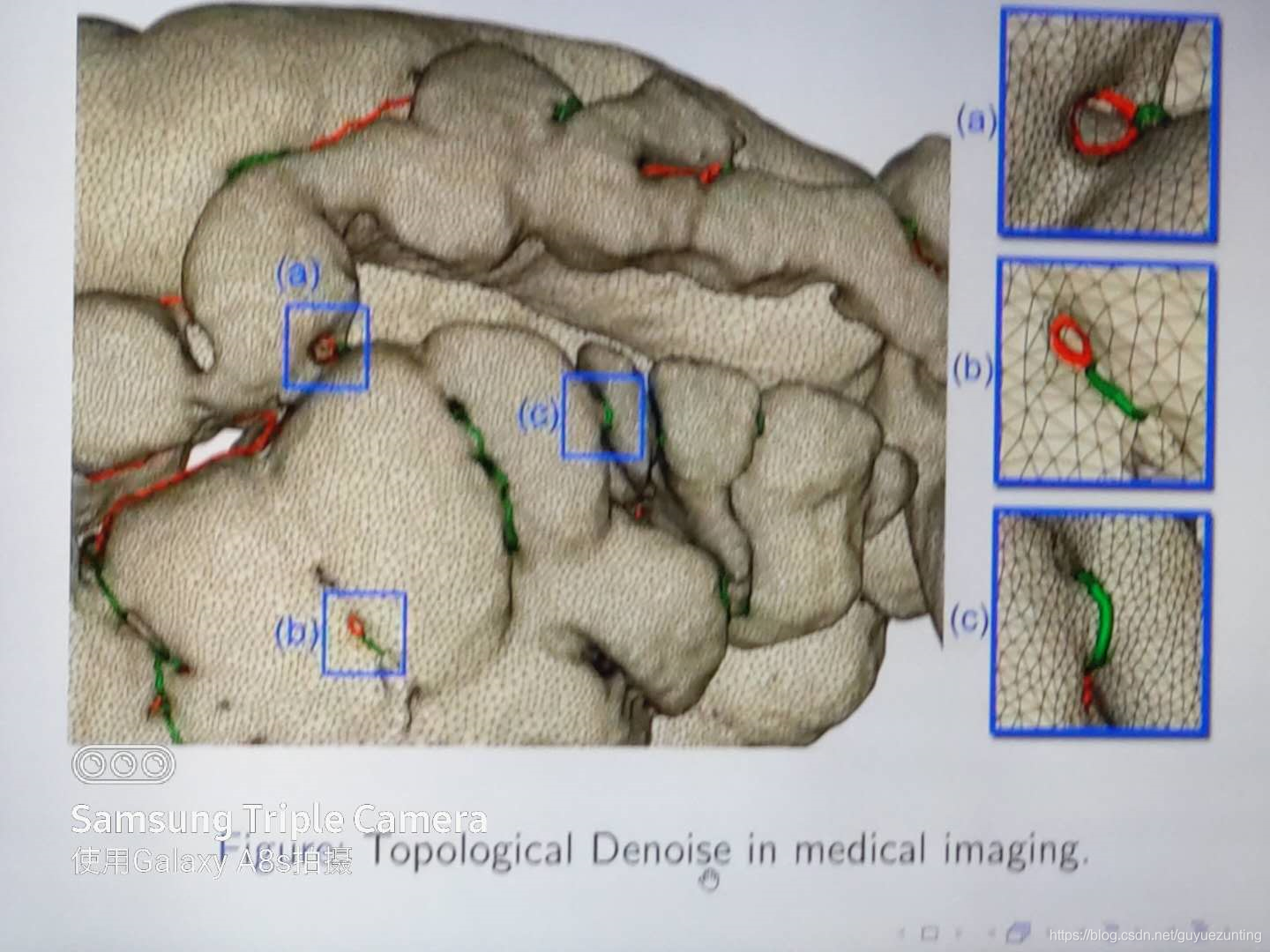 如图所示：在医学图像上。我们经常需要通过医学图像来重建器官的曲面。这边显示的是人的一段大肠。直肠曲面。我们用ct得到的是很多直肠的切片。然后用图像segmentation的方法。把图像分成内部和外部。在边缘处建立曲面。但是图像处理的话。经常有大量的错误，如果一个像素出错。就会使整体的曲面拓扑发生错误，所以大肠通常使桶装的，拓扑非常简单。但是数值处理之后有很多虚假的这种环柄圈和隧道圈。这些虚假的地方用人眼非常难以看到。所以必须要用计算拓扑的方法。找到这些圈。

如图使真实数据生成的大肠曲面，用人眼很难看到曲面上的环柄圈以及隧道圈，但是电脑可以轻易的识别出来。很多圈藏在曲面内部，如果不用计算机的话对于真人来讲使没有可能查到的。但是用计算机可以很容易找到这些虚假的地方。西门子癌症检测技术中。都用到这个方法。

 基本程序库，

philosophy

代数拓扑的主要思想。给一个拓扑空间。我们的空间定义各种各样的群。通过研究这些群的性质。来反映出空间拓扑的性质。换句话说我们位拓扑空间拍了一张照片，照片的底片是代数的，代数这个词和算法这个词是同义的。都是可计算的意思。代数的好处是可以用计算机来处理。拓扑问题很复杂。好多时候只能依靠人类的想象。但是有一个concrete实物能计算的话。就把这个难度降低了。但是这个过程。没有办法把所有的结构保持。所以会丧失掉一些信息。所以这是代数拓扑的一个能力的缺陷。所以这是它背后总体的一个思想。

最重要的就是fundamental group基本群的概念，基本群就是在曲面上固定一个点。然后考察经过这个点的所有的曲线，所有的圈，然后这些圈。在同伦homotopy意义下的进行分类。这些同伦类，构成一个代数结构的所谓的群上。然后这个群的话。我们可以看到原来拓扑的一些信息。

如图所示。什么叫同伦呢？上图显示了一个实例。我们得到一个映射。从0，1这个单位区间。映射到曲面上。得到曲面上的一条路径。如果我们能把这个路径从一条逐渐的变化到另外一条。不离开这个曲面。我们说这两个曲线是同伦的。后面数学定义又说，从曲线1开始到曲线2终了（这里其实是曲线1的形状是起点，变换成曲线2是终了，并不是沿着曲线路径从1到2），（后面是错误理解）这不就是圈么。如果两条曲线形成一个圈，那么方向势必相反，如果方向相反又如何逐渐变换到另一条曲线呢，后面又扯什么圈相乘，逆计算的。好奇怪。而且讨论曲线的时候没有方向，讨论圈又有方向，太乱了。

 上图是同伦的数学定义。一条曲线实际是一个单位区间的连续映射，从单位区间映射到曲面上。一个封闭曲线，圈，曲线的起点和重点重合都是base point。如果给定两个曲线。连接他们的话有一种曲线。从第一个曲线开始到第二个曲线终了。当我们变换同一个参数的时候。会得到不同的光滑曲线，如果这个映射整体存在的话。我们说这两条曲线彼此是同伦等价的。（问题，为什么要连接，怎么连接，不是逐渐变换么。一团乱麻，错误理解）这里描述确实有点疑惑，经查证，应该是曲线1是一个形状，曲线2是一个形状，这里描述的连接他们的曲线，其实就是从曲线1通过一种变换，逐渐变换成曲线二时这些曲线运动的路径，为同伦。例如f(0,t)=γ1（t）即从γ1开始变换t为中间态，如果t为1时，则变为γ2，f（1，t）则为从γ2变为γ1的路径中间态，t为0则变成了γ1，因此才有了后面的互为同伦等价。

（这一段时错误理解）从上图看到描述同伦的时候，F（family）：[0,1]x[0,1]是两个loop的乘积，根据后面描述的乘积来看，相乘之后两个曲线形成一个loop。更改t只是修改了起点终点，因此可以说成，如果两条曲线同伦，那么他们经过同一个点。并且乘积成立。讨论loop乘积的时候前提是他们同伦。乘积之后更改t，形成的新曲线，只是更改了两个loop所占的比例

非常容易证明，如果第一条曲线和第二条曲线同伦，当且仅当第二条曲线和第一条曲线同伦。所以我们可以把曲面上所有的圈根据同伦分类。每个类用方括号表示[γ]，我们定义个两个圈的乘积。

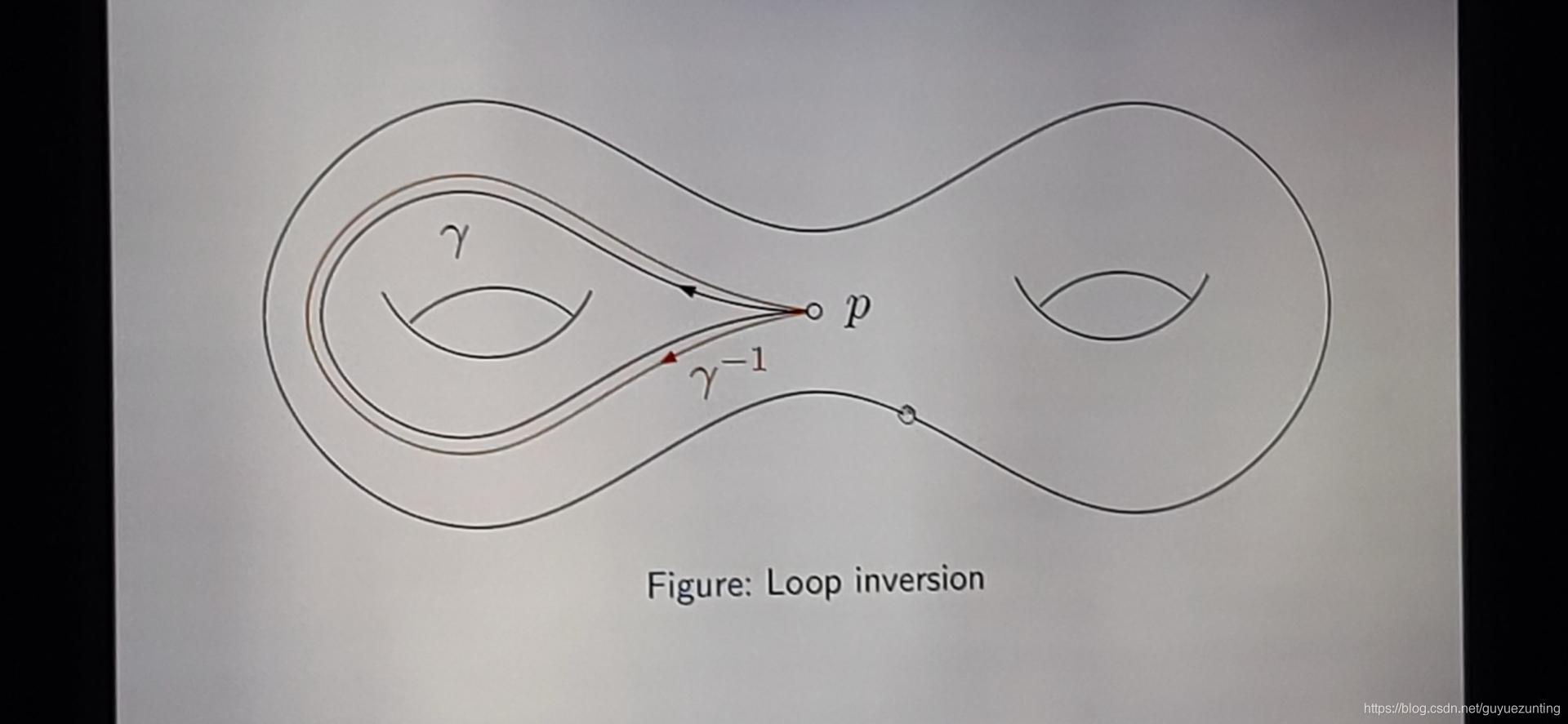
，和一个圈的逆，如下图所示。给一个圈，它是从黑线开始走，离开p再回到p。逆就是方向取反。 

 数学表示，就是

下图表示两个圈的乘积：

乘积就是。我先沿第一个圈走，然后回到起点，然后从起点沿第二个圈走。然后这两个圈首尾相连。得到一个大的圈。大圈被称为两个圈的乘积γ0*γ1.数学上看，给定两个圈。构造一个大圈。前一半沿着第一个圈走，后一半沿着第二个圈走。首尾相连，如果是逆的乘积呢？曲线的乘积呢？曲线的逆呢？明明在讲曲线。什么玩意儿。

 

fundamental group

如下图所示：我们给了基本群的一个严格定义。给一个拓扑空间。大多情况下是manifold流形。道路连通的。我们固定一个base point p。考察过这个点所有的圈，将这些圈。根据同伦关系进行分类，然后我们用圈乘积的类来定义类的基。用圈的逆，定义类的逆。来看一个特殊的圈，这个圈一直没有走一直在基点p上。这样的圈构成了所谓的unit element。换句话说任何一个圈，在曲面上，如果能缩成一个点。都属于这个类。所以[e]代表所有能缩成点的圈。可以证明所有这些同伦类构成了一个群。这个群构成曲面的基本群。（如果是点云的话，是否是曲面上所属的点则为这个曲面的基本群，如果有一群点云，不同曲面上的点，即为不同的基本群，以此可以进行分割，同一个曲面也会出现不同基本群，如环柄）

fundamental group representation

基本群很抽象。在计算机上如何表示，如何处理。我们有一个用符号的方法进行表示，我们考察英语构成的词汇。这个词汇都是由字母生成的，任何一个词汇可以表示成一串字母。所以我们把字母称为生成源。abcd一直到z称为生成源。那么一个词可以称为一串字母。这边的话，每个算法i都属于生成源。但它有个power，这个power是什么意思。如果你的字符串中。连续出现了三个a。就可以写成a^3.所以所有的词都可以用下图表示。有的词是空的，称为单位源，这里字母g为生成源

 还有的词是空的，这种词被称为单位源，unit element

两个词的拼接动作，被称为乘积。

取逆的话，是对字母逆序，指数取负

这些域片（后面隔开基本域形成的域片）之下？。这些词构成一个自由生成的群，称为词群。

word group

我们定义一些特殊的关系。每个关系是一个词。所以你有有限的词。我们说两个词彼此等价。如果可以从第一个词通过有限步变成第二个词。每一步是两种基本操作中的一种。有点像平衡二叉树的查询路径，不同的路径有不同的字母顺序。第一种基本变化是在一个词的任何一部分插入一种relation。或者在一个词中发现一个子串等于某一个relation你把它去掉，那么第一个词能通过这两种变换变成第二个词，我们就说，这两个词是彼此等价的。

 引入这个关系之后，我们把词进行分类。所有这些词类的话，关于刚才定义的首尾相接，依然成群，这个群的话被称为词群。那么在计算机上表示的话，词群有两部分。第一个是所有的生成源，第二个是所有的关系。这个群可能非常大，里面有无穷多个元素，但是它的生成源很少。relation也非常少。如果这个群没有relation。那么我们就说这个群是自由生成的。那么曲面的基本群的话就是，用这个方式来表示。其实这里的字母就是圈，词就是沿着圈（生成源）以某种关系组成基本域切割顺序组成的关系。一种关系代表一种类，这些类组成了群。

 我们下面是。如何表达曲面的基本群。曲面基本群有一个非常漂亮的结果。叫做典范基本群表示，先定义曲面的相交数。给定曲面上两条直线γ1和γ2相交于q点，他们的切向量，即分向求导叉乘得到的新的向量跟q点的法向量角度小于90°即点乘和大于0，等于0为90°，如果与法向量平行则为正1相交index，如果相反则为负1，如果法向量是相切的我们说他们的index为0，我们就可以对每个交点定义一个指标。

如图 ，algebraic intersection number一个曲面上给定两个圈γ1和γ2.我们考察所有的焦点，然后把所有焦点的相交指数intersection index加起来，得到一个数。被称为这两个数的代数相交数。

代数相交数同伦不变性定理：

如图意思是这样的，两个曲线的代数相交数在同伦变换下不变。我们把红色的曲线γ1，变成蓝色的，这样曲线的形状发生了改变。红色的γ1跟γ2有四个焦点，但是中间中间的两个相交数互相抵消，因此虽然形状发生变化导致交点数目发生变化，但是代数相交数没有发生变化。所以代数相交数可以定义在曲线的同伦类上。

这边显示的是亏格为2的一个曲面基本群的生成源，每个handle上有两个曲线，一个是a1和b1一个是a2和b2.我们如果沿着a1切开这个曲面。沿着箭头走，保证切痕在右手边。右侧是悬崖，左侧是曲面。走到a1的q点的时候再沿着b1往回走，等再到q点a1反向走再到q再沿着b1反向走，然后a2和b2一样走，这样得到一个右边的八边形

如果用代数来描述的话，我们为每个环柄上找到两个圈，ai，bi，ai和bj的相交数为1，如果i==j.如果i！

=j，为0.不同的ai代数相交数为0，不同的bi代数相交数为0，如果我们找到这样的圈，我们就把他们称作曲面基本群的一组点算基底，从这个图上来看，这个点算基底，是非常有规律的，但是，这个曲面上有无穷多种点算基底。

我们得到基本群的表示，每个handle上有一对a和b，然后它只有一个relation，只有一个关系式。关系式就代表切开这个基本域的边界，它能缩成一个点。这个基本域的话他的边界非常有规律，每个handle产生四个词上，这四个词用中括号表示。这是一个基本定理，下面证明这个定理。

 

如图所示：这边的话，显示的是另外一种点算基底。我们看a1和b1只有一个交点，a1是隧道圈，b1是环柄圈。a2和b2也只有一个交点，a2是不是隧道圈也不是环柄圈，是曲面上的圈，b2是环柄圈。a1和a2以及b2没有交点，a2和a1以及b1没有交点。他们之间即环柄的源之间相互没有交点。原来我们说，每个handle其实代表一个洞，这边我们看，h1和h2分别代表一个洞，其实整个外面区间h3也是一个洞。其实a2，b2围绕的是h3这个洞。所以这个洞这个概念是人为的一个概念。并不是本质的一个拓扑的概念就曲面而言。如果我们想定义什么是确切的洞，必须加上嵌入，R3这种系统。

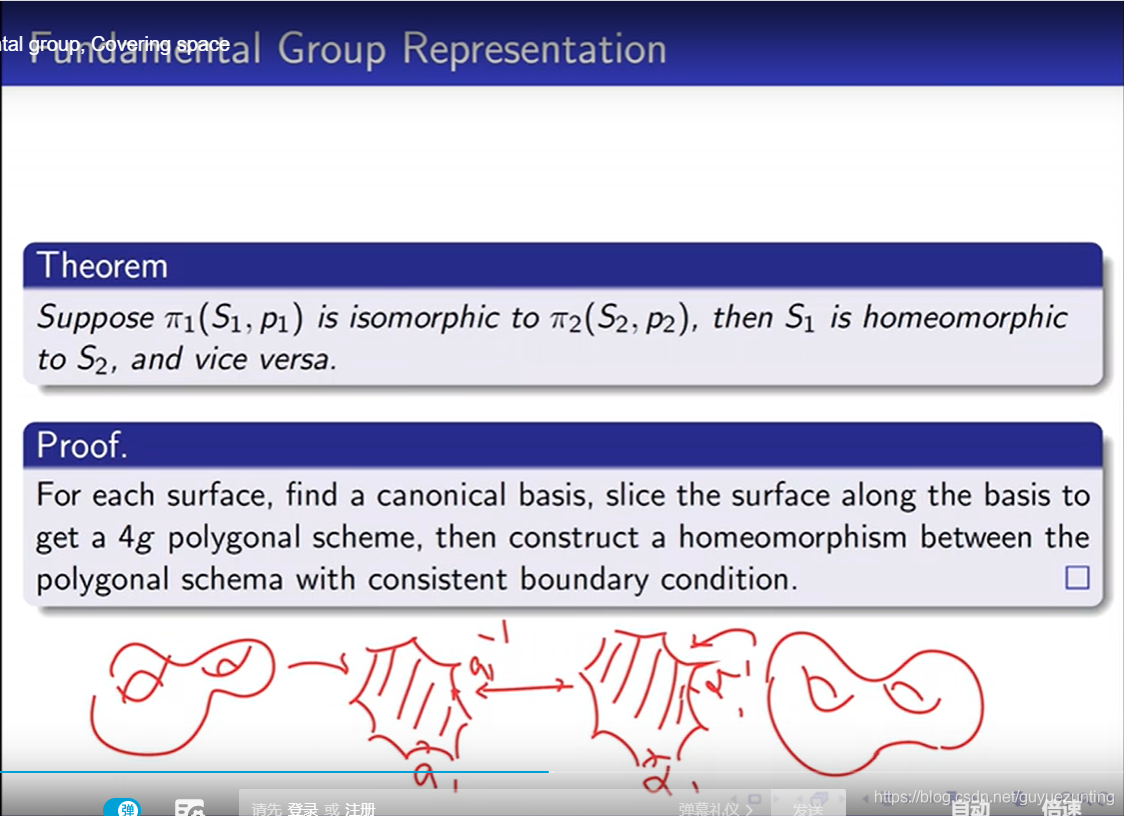
有一个基本定理。如果两个可以紧的可以定向的曲面，他们的基本群，彼此同构，那么他们拓扑等价，存在一个拓扑同胚在他们之间，证明的话非常。通过这个群的话可以变成点算形式。然后通过点算基底把他切成4g的polygonal shceme（多边形形式），然后在平面上找到他们两个平面的多边形之间的映射。但是一定要小心边界条件，一定要设置好，第一个是a1对应到另一个平面映射，也是a1.顺序不能乱。如果你要想求两个高亏格曲面的注册。那么这个实例证明（同构）也给了计算算法。

在计算机视觉中。这个拓扑复杂曲面的注册也用的是这种方法。但是困难就在于找到这个canonical basis（点算群，典算群）。

这个定理非常有用。

范坎彭（Seifert–van Kampen）定理。他实际是给了一个分而治之的一个方法。说，你给了一个比较大的流形，我把它切成两块。用u，v来代替。然后他们相交的话是。w。然后我分别算u，v的基本群。然后再算他们相交部分的基本群。要求u，v，w都是道路连通的，这一点要注意，在实际计算中。然后的话，我们通过这个三个小的基本群。可以拼成原来这个大的基本群。我们只要把u的生成源拷贝出来，v的生成源拷贝出来，把u的关系拷贝出来，v的关系拷贝出来，然后这个相交部分的所有的关系把它扔掉，但是相交部分的每个生成源，它既在u里面也在v里面。在u中有一个表示，在v中也有一个表示。这两个表示的话，是彼此等价的。所以的话，相交部分的每个生成源。会得到一个新的关系。这样我们可以分而治之。把这个复杂的空间分成两半，每半再分成两半。然后这样的话就可以递归的算出来原来空间的基本群，这个方法对于算法设计是非常本质的。

这边的话呢，我们给出曲面的一种构造方法。叫做连通核。或者连接核。你有两个曲面。然后你从第一个曲面扣掉一个小圆盘。从第二个曲面上扣掉另外一个小圆盘。第一个圆盘的边界是一个圈D1，第二个小圆盘边界也是个圈D2。圈和圈的话找到一个映射。这样的把，你把圈D1上的一个点跟另一个圈D2的对应的一个点粘起来。粘好之后就得到一个封闭的曲面。这个曲面的话是个亏格为2，这个操作的话被称为连通核。相当于是上图中分开的曲面，先各自扣个圆盘，然后再沿着圆盘把两个曲面缝起来，就变成了一个亏格为二的曲面，上图中箭头指向的曲面。不同的曲面可以通过连通核连成一个封闭的曲面。

曲面论的话有一个基本定理。所有的紧的可定向的曲面可以看作是很多torus（圆环面）的连通核。每个torus（圆环面）一个genius，当然不可定向的曲面的话我们要加一个特殊的东西。射影空间，现在可以不用太考虑这种情况。

上图是证明拓扑环带。它的基本群的话。是由a，b生成。然后只有一个relation aba-inverseb-inverse那么我们把这个曲面沿ab切开。撑开撑到平面上。我们得到一个平面的四边形。这个四边形的话四个角点是p。它的边界的话是aba逆b逆。然后这个边界的话能生成一个点所以我们得到关系式怎么证明所有的圈都是由ab生成呢？第一个，如果这个圈和ab有交点。我们先同伦变换这个圈。使得这个圈和ab所有的交点都在p上。然后我们再把这个圈分成一系列的小圈。变成γ1γ2...γk。每个γi它从p点出发p点结束。但是中间的话它和ab没有其他交点。那就意味着这个γi的话。可以被运用成这个长方形的内部，然后它和边界没有交点，只跟角点有交点。然后它肯定是从某个角点出发。到另外一个角点中止，所以它可以deform到四边形的边上。所以的边的话都是a，b，a逆，b逆。所以γi可以用a、，b来生成。原来的daγ是这些γ的乘积。大γ也是由a，b来生成。这样就证明了，torus的确是通过ab来生成的有一个relation。这是第一步。

第二步的话，在torus上扣掉一个圆盘，相当于是在平面长方形上扣掉一个洞。把这个洞扩大扩的非常大。把长方形内部都蚕食掉。最后剩下的始什么呢，剩下的就是这两个圈，a，b。实际是个图，给一个图的基本群是自由生成的。图的基本群就是它没有relation。因为任何圈的话。它要想缩成一个点。一定要有一个面积，有个二维的东西。一维的图上没有二维的patch，所以它没法生成一个点。我们证明了，torus扣掉一个点之后的话他的基本群是<a,b>

这边的话，我们先看亏格为2的曲面。如何证明。我们拦腰通过γ砍一刀。把它分解成两部分，一边有一个handle。刀痕的话是一个圈γ。T1,T2 ，右边的话是一个tunnel轮胎去掉一个disk。左边也是一个轮胎去掉一个disk。所以根据刚才的原理。右边的基本群是，左边的话，基本群是，中间的话是他们相交的图γ应用capture section定理的话。

T1∪T2等于原来亏格为2的曲面。它的生成源T1和T2的生成源的并。它的生成源是由γ诱导的。γ的话，它既属于T1又属于T2。那么在T1中的话。γ等于四边形的边界。同理在T2中，等于边界所以γ有两个表示，这两个表示等价。并到一块儿的话得到一个关系式，再次证明，亏格为2的情况下主定律是成立的。然后我们可以用数学归纳法。对于任意亏格g，它都是对的；

大家可以做一个作业。把这个原则证明一下。假设g-1个亏格的情况下是对的，然后增加一个handle，然后用同样的argument。

这样的话我们就证明了。曲面基本群的点算表示。那么如何计算呢。下面进入computational topology（计算拓扑）基本群

cut graph第一步我们要计算所谓的切图。就是说这个曲面上，有这样一个切图，把它切下去之后的话，曲面可以展开成一个拓扑圆盘。这是cut graph的定义。这个红线的话就是这个切图。曲面的话沿着切图切开的话。就得到一个disk。得到一个单连通的亏格为0的曲面。然后只有一条边界。怎么算呢。你可以想象，这个曲面上布满了干草。然后随便选一点开始放火。这个火焰的话就在曲面上蔓延。越来越大。然后火焰的前缘会在一些地方相遇。相遇的话，火势就会熄灭。那么火焰熄灭的地方，给了我们这个cut graph。所以这个是这个算法的一个很直观的描述。我们叫火烧法。在数学上也叫，你从一点出发。发出测地线，测地线（geodesic）（有人问，拓扑没有度量，哪有测地线，是默认三角形全等了吗？）往前走，越走越大。这个测力线的前缘会彼此相遇，相遇的地方被称为cut graph。

火烧的时候呢，它只能均匀的往外扩展，然后烧过的区域的话肯定拓扑圆盘。它没办法跳跃。这样的话，直观上，我们保证下面你扒开之后？得到的确实是一个拓扑圆盘。并且这个算法呢穷尽了所有的二维的面积。剩下的就属于一维的图。这就是给算法一个只管描述。

下面用计算机说一下。cut graph算法非常简单，就是说。你的输入是个三角网格。然后我们要算它的对偶。所谓对偶就是说。我们算每个三角形的中心。把这些中心连接起来。每个边就得到一个对偶的边。原来三角形的每个顶点变成一个面。原来三角网格每个面变成一个顶点。就是描述了所有的三角网格的中心围着他们的公共顶点形成新的面，原来的三角网格面则变成了这些中心点。每个边还是变成一个边。这样我们得到另外一个mesh （叫做M拔）有了M拔之后我们把它看成一个graph。算它的生成树（T拔）然后我们看这样的边，就是这些边的话。不在这个T拔上，这些边的对偶的边在原来三角网格上。构成一个图就是cut graph。算法非常sweet 也比较高效。（参考网格最小生成树算法），就是说当你得到cut graph之后。

第二步要计算基本群的生成源。就是那些圈。这些圈的话，实际就相对容易算了。

这边的话我们用火烧法来算cut graph。算出它的切图。有了切图之后，再算基本群的基底。

如上图，是整体算法。第一步先算输入网格的切图。这个切图也是一个图。那要计算这个图的生成树。T图去掉这个树之后会剩这些边。每个边加到树上。它肯定是unique的圈γi。每个边生成一个圈，你把这些圈都收集起来。这些圈的话就是原来三角网格的基本群的生成源。那大家可以用这个 范坎彭（Seifert–van Kampen）定理来证明这个算法是对的。当一个家庭作业做一个思考。也可以编写这个程序。这个程序写完之后要想这个程序为什么是对的。用今天讲的范坎彭（Seifert–van Kampen）定理来证明。

下面来获取关系，上一步获取了生成源。

基本群的话有两部分，一部分是得到生成源，一部分是得到关系。如何算关系呢？首先还是计算三角网格的cut graph  。然后计算生成树。T，cut graph减去生成树的话就剩边。这些边是有定向的，这些定向的边。和对应的基底的圈。定向相同。然后把三角网格。沿着cut graph 切开。且完之后的话，你得到一个基本域M拔（）或者叫多边形。是一个拓扑圆盘。看它的边界。他的边界的话是围着这个走了两次。然后把它的边界记成小γ。然后我们在γ上行走。依次行走，每当我们碰到这个eI（边界）我们就加上一个γi如果碰上ei的反向则γ加上反向。那么我们从起点重新走回来之后的话回到起点。就会得到一个词w，这个词w开始设为空，这个词的话。就是基本群的关系。由此我们得到了生成源以及关系。就得到了基本群的一个表示。但这个表示的话。并不是典型的canonical的。要算典范的话。比这个要复杂一些。

第三个算法。切图，生成源，还有关系。加在一块儿，给出封闭曲面的一个基本群的表达。但是这个表达不是典范的canonical。它比典范要复杂。那么你得到这个基本群的一个表示。这个计算时间的复杂度是线性的。非常简单。但是同一个群它有不同的表示。你判断这两种表示是不是彼此等价。这个算法是特别难的问题。这也是为什么这个计算拓扑。本质上讲，大部分都是比较难的。

上图的话，我们显示一个覆盖空间的概念。我们周期性的把这个小猫铺到平面上。平面上任何一个点。你可以把它映回到小猫相映的点，这个映射的话有这样一个特点。小猫身上你随便取一个顶点。然后找这个点的邻域。这个邻域的原像的话有无穷多个。这些无穷多个原像的话。彼此是分离的。然后选定其中的一个原像。然后刚才的映射现在是平面的限定的小区域到小猫身上的小区域他是同胚的。是一一映射。并且是onto，并且是光滑的。这种情况下，我们说这个平面空间式这个小猫空间的覆盖空间。小猫是底空间。这个映射叫投影映射。总体上看的话。这个投影是平面上多对小猫一的。但是局部上看，是一对一的。

下面看一个特殊的映射。我们把刚刚周期的平面小猫进行错动，把相邻的小猫映射到下一个小猫上。整体错动，错动之后，平面上的小猫对应左边空间的小猫还是一一对应的。整体错动并不影响投影映射。这种投影是不变的。整体这种错动的话被称为甲板映射。deck projection。或者叫覆盖映射。覆盖变换。

如上图所示，覆盖空间有个基本群。底空间有个基本群。覆盖空间还有一个加班映射群。这三个群是有确定的格式的。这个投影映射的话，把覆盖空间的基本群，映成了底空间的基本群的子群。那么这个商值。和覆盖空间的甲板映射群是同构的。这个式子是优美的代数表示拓扑的例子。

有一个特殊的空间，叫万有覆盖空间。万有覆盖是单连通的。它上面所有的圈都能缩成一个点。在这种情况下根据覆盖空间定理，上一张图片，分母这个时候是e。因为都能缩成一个点，所以是典范基本群e。这个时候底空间的基本群和覆盖空间的甲板映射群。是同构的。所以刚刚看的小猫的例子。周期覆盖空间的所有的圈都能缩成一个点。所以是单连通的所以覆盖空间是小猫的万有覆盖。 

上面我们显示的是一个比较费解的情况。远离了人们正常生活经验。高亏格曲面的话，我们可以用典范基底把它切开。切开成一个八边形。然后我们把这个八边形粘起来。比如棕色跟大红色的边，棕色的边是a1，大红色的边是a1 inverse。粘完之后配一个双曲度量。可以不停的粘下去。所以每个顶点处。有八个copy。每个顶点处粘8个copy。所以棕色是第0圈，大红色第1圈，等等。所以往后走的话。这个每圈。copy的数目是指数增长，但是你可以证明，不停的粘下去之后，你会发现，它会覆盖真个open的单位的圆盘。所以单位圆盘。就是左边的万有覆盖空间。但是这个问题非常难以计算。因为size是指数级减小的。所以只要往外走出超过两三层。就完全超过机器长度，机器就没办法算了。所以双曲几何和高亏格的曲面非常困难。机器精度跟不上。

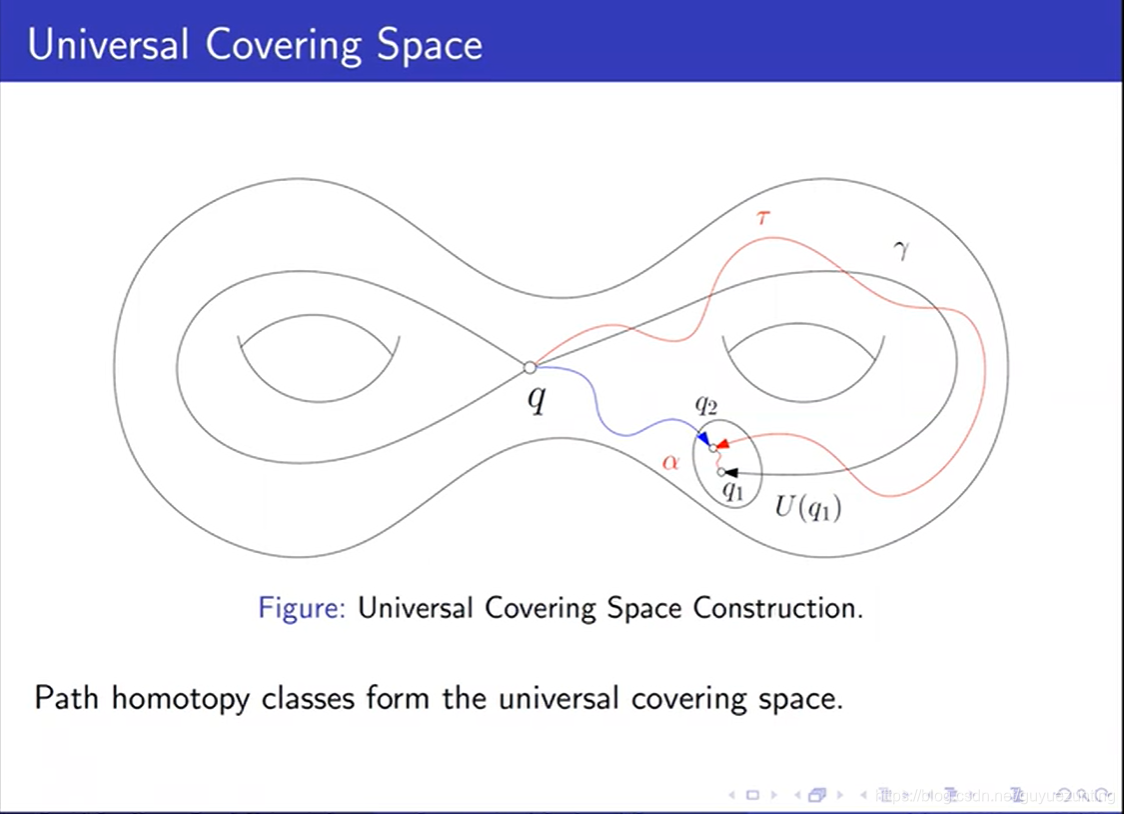
上图是万有空间。的一个严格证明，证明万有覆盖空间的存在性。但是这个证明特别抽象。下节课讲。基本想法是。我固定q点，然后考虑曲面上所有的路径。路径的终点是，然后所有路径的同伦类构成一个抽象空间。这个抽象空间就是曲面的万有覆盖空间。所以证明手法非常抽象。但是一旦懂了之后是非常有用的。

下面给出万有覆盖空间计算机算法。 我们知道万有覆盖空间本身是无穷大的。所以我们只能计算他的一个有限的区域。第一步是把M上的cut graph先算出来。算完之后，因为它是个图。可以分解成很多段。很多边。和很多顶点。所以每个边是一系列小边的一个组合。然后把M沿着切图切开。的到一个基本域M拔。然后把覆盖空间进行初始化。直接拷贝M拔就是基本域。然后在覆盖空间的边界上。随便找一个segment s1.就是很多段中的一段。然后得到一个新的拷贝M拔的新的拷贝，把新的拷贝，和当前的covering space粘起来得到。然后在M拔上取si。M曲线的边界上取si的inverse把他们俩粘合起来。粘合之后。追踪覆盖空间的边界。它的边界上有可能出现相邻的两个segment。这两个相邻的segment彼此是inverse的。然后把他们粘起来。然后不停的重估4，5直到稳定。这样得到一个更新后的covering space。知道得到的portion足够大。这个时候停止。