决策树系列3：信息增益、增益率、基尼系数 (史上最详尽)

引言

上回说道，决策树最核心的部分是如何选择最优划分属性，今天我们看看经典的三种最优划分算法。

本次内容是决策树的核心，《大数据茶馆》力求做到通俗的前提下推导细致、循序渐进、全程举例，希望可以帮助大家彻底理解这三种方法的来龙去脉。

---

决策树回顾

上一篇文章的例子中，小明和小亮根据各个属性判断是否适合打球列了表格，并给出了一棵决策树。

如上篇文章所说，第一个节点选择场地进行分支划分一下子决策了三条数据(1,2,3)，而如果选择风力来划分则无法决策数据，过程会变得复杂许多。所以选择哪个属性进行分支划分就很关键了。

最优划分标准：我们希望每次选择的属性可以让划分后的分支数据更有区分性，使各个分支的数据分类纯度更高，最好是每个分支的样本数据尽可能属于同一类别。

常用的最优属性选取方法有三种：

• 信息增益：在 ID3 决策树中使用
• 信息增益率：在 C4.5 决策树中使用
• 基尼系数：在 CART 决策树中使用

下面我们依次来讨论。

我们以"场地"属性进行划分为例，讨论这三种方式分别如何计算划分前后纯度的变化。(一个属性弄清楚后，依次计算每个属性划分的纯度变化，选择最优的属性划分即可)

下面是我们将用到的"场地"划分的基本数据。

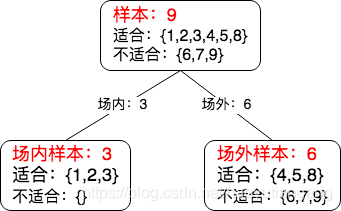
• 划分前: 样本 9
  • 适合：{1,2,3,4,5,8}，占比 6/9
  • 不适合：{6,7,9} 占比 3/9
• 按类别划分后：
  • 室内样本 3
    • 室内适合：{1,2,3} 占比 3/3
    • 室内不适合：{} 占比 0/3
  • 室外样本 9
    • 室外适合：{4,5,8} 占比 3/6
    • 室外不适合：{6,7,9} 占比3/6

一、信息增益

ID3 决策树采用信息增益选取最优划分属性。

1. 回顾信息熵

我们在第一篇文章《聊聊信息熵》中学到了信息熵，熵反映了事件的不确定性，对于一般分布事件而言，熵是各种可能性的熵以概率为权重进行加和。(各个可能性的熵可以用 $logm=log\frac{1}{p}$ 来表示）所以熵的公式为：

$$Ent(X)=-\sum _{x\in X}p(x)logp(x)$$

2. 从熵说到信息增益

属性划分的标准是让每个分支纯度更高，最好是每个分支的数据尽可能属于同一类别，其实就是尽可能增加分类的确定性。而熵表示了事件的不确定性，消除熵可以增加事件的确定性，所以只需计算划分前后熵的变化就可以了。

1. 划分之前计算事件的熵：Ent(X)
2. 按照属性 A 划分后再次计算事件的熵：Ent(X|A)
3. 则 Ent(X) - Ent(X|A) 就是划分之后熵被消除了多少。

其中 Ent(X|A) 称为条件熵，就是在 A 分布条件基础上的 X 的熵。

因为信息与熵大小相等意义相反，所以消除了多少熵就相当于增加了多少信息，这就是信息增益的由来。

所以信息增益：Gain(X,A) = Ent(X) - Ent(X|A)

熵Ent(X)我们都会计算了，下面我们看看条件熵 Ent(X|A) 如何计算。

3. 求解条件熵 Ent(X|A)

属性 A 本身是有分布的，我们这里"场地"的分布为"室内"和"室外"。

整体的条件熵就是A的各个分支(室内、室外)自身的条件熵以分支概率为权重进行加和。

$$Ent(X|A)=\sum _{a\in A}p(a)Ent(X|A=a)$$

# 场地" 划分举例：

Ent(X|场地) = 
    p(室内) * Ent(X|场地=室内) 
    + 
    p(室外) * Ent(X|场地=室外)

公式中p(a)已知，下面来计算 Ent(X|A=a)

已知熵的公式为 $Ent(X)=-$