零阶保持器（ZOH）与一阶低通滤波器频率特性分析

1.零阶保持器（ZOH）频率特性分析

零阶保持器传递函数：

画 Bode 图进行频率分析：

s=tf('s');
T=0.0002; %采样周期0.0002s
G=(1-exp(-T*s))/s;
bode(G);

从图中可以看出：随着频率 ω 的的增加，当 ω 在 10000 附近时，零阶保持器的幅值和相位开始发生跳变。

• 幅频特性中，幅值达到最低时立即发生跳变至最高，保持稳定后再次跳变至最低，如此往复；
• 相频特性中，相位滞后，在 −180到−0。 之间呈锯齿状变化；
• 从图中可以看出，零阶保持器是一个低通滤波器，但不是一个理想低通滤波器，高频信号通过零阶保持器不能完全消除，同时产生相位滞后。

2.一阶低通滤波器频率特性分析

​    

画 Bode 图进行频率分析：

T=0.0002; %采样周期0.0002s
fc=1;
A=2*pi*fc*T;
s=tf('s');
H=(1)/(A*s+1);
bode(H);

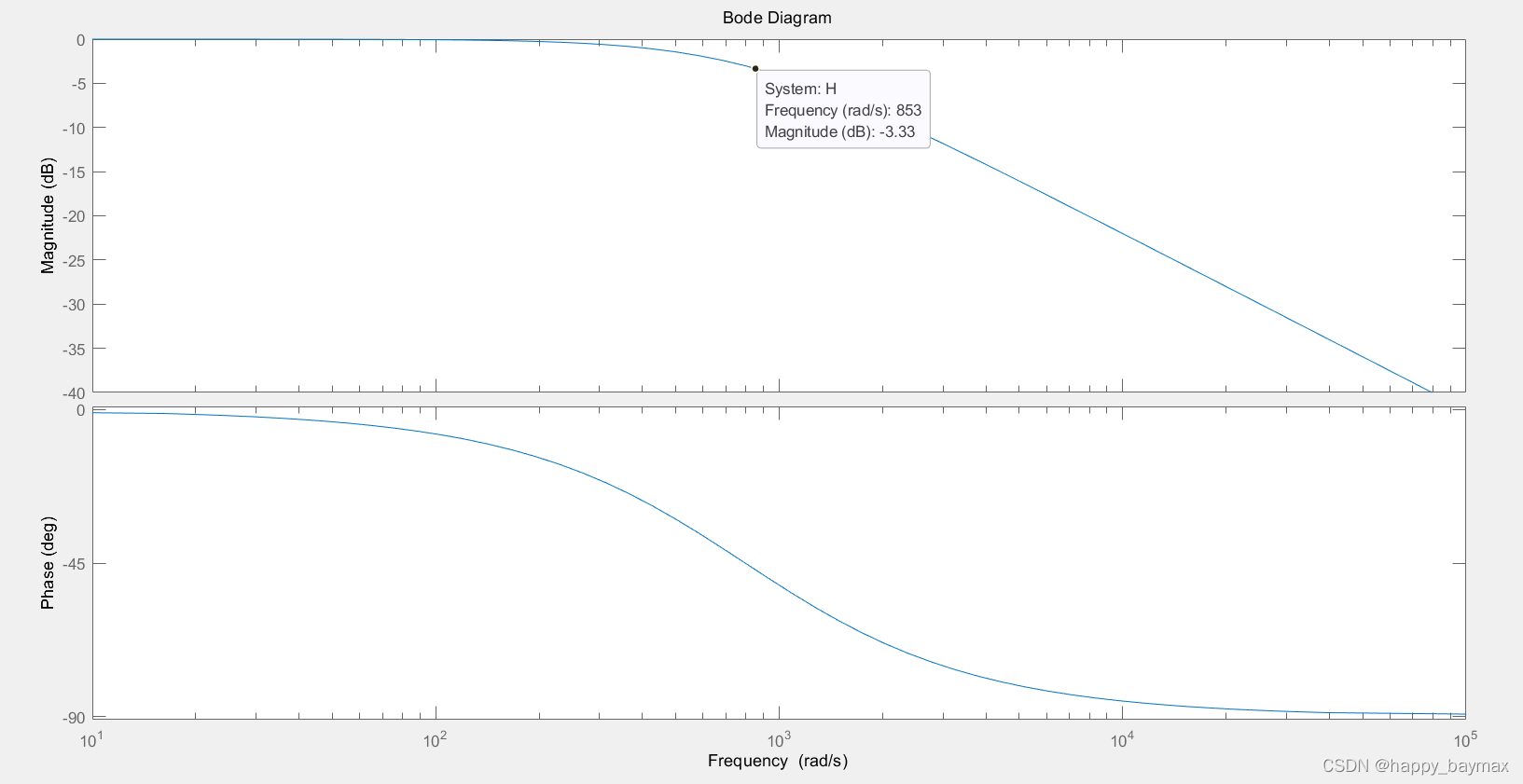
 从图中可以看出：随着频率 ω 的的增加，当 ω 在 853 附近时，一阶低通滤波器开始衰减

到-3db.

 50hz幅值10信号叠加 0.5hz幅值1信号，截至0.5HZ,黑色为低通滤波器后波形，红色为原始叠加信号

function y = LPF(u)
Ts = 0.0002; %采样时间
fs = 1/Ts; %采样频率
fc = 0.5; %截止频率
alpha = 2*pi*fc*Ts/(1+2*pi*fc*Ts); %滤波系数
persistent uo1
if isempty(uo1)
    uo1=0;
end
  uo1= alpha*u+(1-alpha)*uo1;
y = uo1;