数据降维PCA、LDA、t-SNE介绍

数据降维PCA、LDA、t-SNE介绍

来源：降维互动介绍 — Interactive Intro to Dimensionality Reduction (kaggle.com)

简介

1. Principal Component Analysis ( PCA ) - Unsupervised, linear method
   主成分分析 ( PCA ) - 无监督、线性方法
2. Linear Discriminant Analysis (LDA) - Supervised, linear method
   线性判别分析 (LDA) - 有监督的线性方法
3. t-distributed Stochastic Neighbour Embedding (t-SNE) - Nonlinear, probabilistic method
   t 分布随机邻域嵌入 (t-SNE) - 非线性概率方法

方法原理

PCA

来源：PCA and proportion of variance explained by amoeba

以葡萄酒为例，可以通过颜色、浓度、年份等来描述每种葡萄酒，我们可以列出我们酒窖中每种葡萄酒的不同特征的完整列表。但其中许多会测量相关属性，因此是多余的。如果是这样的话，我们应该可以用更少的特点来概括每一款酒了！这就是 PCA 的作用。

PCA 并不是选择某些特征并丢弃其他特征。相反，它构建了一些新的特征，从而很好地总结了我们的葡萄酒清单。当然，这些新特征是利用旧特征构建的；例如，一个新的特征可能被计算为葡萄酒年龄减去葡萄酒酸度水平或一些其他组合（我们称之为线性组合）。事实上，PCA 找到了最好的可能特征，这些特征总结了葡萄酒列表以及唯一可能的特征（在所有可想象的线性组合中）。这就是它如此有用的原因。

这些新的 PCA 特征“总结”了葡萄酒清单时，实际上是什么意思？

第一个答案是，PCA 寻找尽可能多的葡萄酒差异的特性。

第二个答案是，PCA 寻找能够尽可能重建原始特征的属性。

PCA 的这两个“目标”听起来很不同！为什么它们是等价的？

让我们选择两种葡萄酒的特征，也许是葡萄酒的黑度和酒精含量——我不知道它们是否相关，但让我们想象一下它们是相关的。以下是不同葡萄酒的散点图：

可以通过画一条穿过这个“葡萄酒云”中心的线，并将所有点投影到这条线上来构建一个新属性。这个新属性将通过线性组合w1x+w2y来表示，其中每条线对应一些特定值的w1和w2。

PCA 会根据什么是“最佳”的两个不同标准来找到“最佳”线。首先，沿着这条线的值的变化应该是最大的。注意线条旋转时红点的“分布”（我们称之为“方差”）如何变化；你能看到它什么时候达到最大值吗？其次，如果我们从新的特征（红点的位置）重建原始的两个特征（蓝点的位置），重建误差应该最小。重建误差将由连接红线的长度给出。观察这些红线在旋转时长度如何变化；你能看到总长度何时达到最小值吗？

如果你盯着这个动画一段时间，你会注意到“最大方差”和“最小误差”同时达到，即当线条指向我在酒云两侧标记的洋红色刻度线时。这条生产线对应于 PCA 将建造的新葡萄酒特征。

为什么这两个目标会产生相同的结果？据说PCA 与特征向量和特征值有某种关系，他们在这张照片中的哪里？

你可以想象黑线是一根实心棒，每根红线是一根弹簧。弹簧的能量与其长度的平方成正比（这在物理学中称为胡克定律），因此杆将自行定向，以最小化这些平方距离的总和。

---

PCA如何从几何问题（具有距离）转变为线性代数问题（具有特征向量）的直观解释是什么？

来源：https://stats.stackexchange.com/a/219344/427743

简述：因为可以用线性代数数学建模为优化问题。

来源：https://stats.stackexchange.com/a/136072/28666

从最大化投影方差的角度：
$$\mathrm{Var}(\mathbf{Xw})={\mathbf{w}}^{\top }{\mathbf{X}}^{\top }\mathbf{Xw}/(n-1)={\mathbf{w}}^{\top }\mathbf{\Sigma w}$$
从最小化重建误差的角度：
$$\begin{array}{rl}{\Vert \mathbf{X}-{\mathbf{Xww}}^{\top }\Vert }^2& =\mathrm{tr}\left(\left(\mathbf{X}-\mathbf{X}{\mathbf{w}}^{\top }\right){\left(\mathbf{X}-\mathbf{Xw}{\mathbf{w}}^{\top }\right)}^{\top }\right)\\ & =\mathrm{tr}\left(\left(\mathbf{X}-{\mathbf{Xw}}^{\top }{\mathbf{w}}^{\top }\right)\left({\mathbf{X}}^{\top }-{\mathbf{w}}^{\top }{\mathbf{X}}^{\top }\right)\right)\\ & =\mathrm{tr}\left(\mathbf{X}{\mathbf{X}}^{\top }\right)-2\mathrm{tr}\left(\mathbf{X}{\mathbf{w}}^{\top }{\mathbf{X}}^{\top }\right)+\mathrm{tr}\left(\mathbf{Xw}{\mathbf{w}}^{\top }{\mathbf{ww}}^{\top }{\mathbf{X}}^{\top }\right)\\ & =\text{ const }-\mathrm{tr}\left(\mathbf{X}{\mathbf{w}}^{\top }{\mathbf{X}}^{\top }\right)\\ & =\text{ const }-\mathrm{tr}\left({\mathbf{w}}^{\top }{\mathbf{X}}^{\top }\mathbf{Xw}\right)\\ & =\text{ const }-\text{ const }\cdot {\mathbf{w}}^{\top }\mathbf{\Sigma w}.\end{array}$$
可以看出，最小化重建误差相当于最大化 ${\mathbf{w}}^{\top }\mathbf{\Sigma }\mathbf{w}$ ，所以最小化重建误差相当于最大化方差，两个角度产生相同的效果 $\mathbf{w}$​ 。

PCA数学建模

如上，给定协方差矩阵$\Sigma$，需要寻找$\mathbf{w}$使得${\mathbf{w}}^{\top }\mathbf{\Sigma }\mathbf{w}$最大，约束条件为$\Vert \mathbf{w}\Vert ={\mathbf{w}}^{\top }\mathbf{w}=1$。

通过引入拉格朗日乘子来完成求解：${\mathbf{w}}^{\top }\mathbf{\Sigma w}-\lambda \left({\mathbf{w}}^{\top }\mathbf{w}-1\right)$​

对上式寻找极值点：$\mathbf{\Sigma w}-\lambda \mathbf{w}=0$​，这个就是特征向量方程。也因此和SVD分解联系起来。

• $\Sigma$​​​是对角矩阵（实矩阵情况下代表是埃尔米特矩阵）。根据谱定理，当A是埃尔米特矩阵，存在标准正交基V，由A的特征向量组成。且A每个特征值都是实数。
• SVD分解在某些方面与对称矩阵或厄米矩阵基于特征向量的对角化类似。然而这两种矩阵分解尽管有其相关性，但还是有明显的不同。对称阵特征向量分解的基础是谱分析，而奇异值分解则是谱分析理论在任意矩阵上的推广。

协方差矩阵$\Sigma$，可以表示为$\mathbf{Xw}$。

$\mathbf{X}$是中心矩阵，那么投影是$\mathbf{Xw}$、投影的方差是$\frac{1}{n-1}(\mathbf{Xw}{)}^{\top }\cdot \mathbf{Xw}={\mathbf{w}}^{\top }\cdot \left(\frac{1}{n-1}{\mathbf{X}}^{\top }\mathbf{X}\right)\cdot \mathbf{w}={\mathbf{w}}^{\top }\mathbf{\Sigma w}$

• 在数学和多元统计中，中心矩阵是一个对称且幂等的矩阵，当它与一个向量相乘时，其效果与从该向量的每个分量中减去该向量分量的平均值相同。

线性判别分析(LDA)

LDA，很像PCA，也是降维任务中常用的线性变换方法。然而，与后者的无监督学习算法不同，LDA 属于监督学习方法。因此，LDA 的目标是利用有关类标签的可用信息，LDA 将通过计算实现此目的的分量轴（线性判别式）来寻求最大化不同类之间的分离。

实现步骤

1. 投影均值

   由于该方法的设计考虑了类标签，因此我们首先需要建立一个合适的度量来测量不同类之间的“距离”或分离。假设我们有一组数据点x属于一个特定类w 。因此，在 LDA 中，第一步是将这些点投影到新线 Y 上，其中通过转换包含特定于类的信息：$Y={\omega }^{\top }x$。

   我们的想法是找到某种方法来最大化这些新投影变量的分离。为此，我们首先计算投影平均值。

   • 相当于类标签作为特征空间，要在新的特征空间里把不同类的样本分离最大化。

2. 散点矩阵和解

   我们现在需要找到一个可以表示均值之间差异的函数，然后将其最大化。就像在线性回归中一样，最基本的情况是找到最佳拟合线，我们需要找到这种情况下的方差的等价物。因此，这就是我们引入散点矩阵的地方，其中散点相当于方差：${\tilde{S}}^2=(y-\tilde{m}u{)}^2$。

3. 选择最优投影矩阵

4. 将特征变换到新的子空间

原理总结

来源：线性判别分析LDA原理总结 - 刘建平Pinard - 博客园 (cnblogs.com)

LDA的思想可以用一句话概括，就是“投影后类内方差最小，类间方差最大”。假设我们有两类数据 分别为红色和蓝色，如下图所示，这些数据特征是二维的，我们希望将这些数据投影到一维的一条直线，让每一种类别数据的投影点尽可能的接近，而红色和蓝色数据中心之间的距离尽可能的大。

t-SNE（t分布随机邻域嵌入）

t-SNE方法自2008年由van der Maaten和Hinton提出以来就得到了广泛的应用。与上面讨论的PCA和LDA这两种线性方法不同，t-SNE是一种非线性、概率降维方法。

方法比较

LDA VS PCA

来源：线性判别分析LDA原理总结 - 刘建平Pinard - 博客园 (cnblogs.com)

相同点：
1)两者均可以对数据进行降维。
2)两者在降维时均使用了矩阵特征分解的思想。
3)两者都假设数据符合高斯分布。

不同点：
1)LDA是有监督的降维方法，而PCA是无监督的降维方法
2)LDA降维最多降到类别数k-1的维数，而PCA没有这个限制。
3)LDA除了可以用于降维，还可以用于分类。
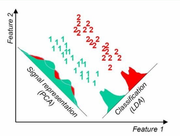
4)LDA选择分类性能最好的投影方向，而PCA选择样本点投影具有最大方差的方向。

这点可以从下图形象的看出，在某些数据分布下LDA比PCA降维较优。

当然，某些某些数据分布下PCA比LDA降维较优，如下图所示：

python实现

# Import the 3 dimensionality reduction methods
from sklearn.manifold import TSNE
from sklearn.decomposition import PCA
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA

'''--------------------------------PCA--------------------------------'''
# Invoke SKlearn's PCA method
n_components = 30
pca = PCA(n_components=n_components).fit(train.values)

# Extracting the PCA components ( eignevalues )
#eigenvalues = pca.components_.reshape(n_components, 28, 28)
eigenvalues = pca.components_

'''--------------------------------LDA--------------------------------'''
lda = LDA(n_components=5)
# Taking in as second argument the Target as labels
X_LDA_2D = lda.fit_transform(X_std, Target.values )

'''--------------------------------t-SNE------------------------------'''
# Invoking the t-SNE method
tsne = TSNE(n_components=2)
tsne_results = tsne.fit_transform(X_std)