一直想弄明白SVD分解后面蕴含的直观意义,可这牵扯到矩阵乘法和线性变换的物理含义的理解。在考虑SVD用途时又牵扯到PCA降维,而PCA降维里又扯到特征值和特征向量。于是,索性全记下来,供诸位探讨学习。
全文将解答如下问题:
一.线性变换经常看到在一个向量的左侧乘以一个矩阵,那矩阵乘法到底有什么样的含义?直观的解释又是什么?文章将从拉伸和基变换两个方面做解释。请重视对线性变换的理解,它对理解特征向量,SVD有很大好处。
二.特征值和特征向量
在我们的直观世界中特征值和特征向量到底是一种怎样的存在?
三.SVD分解
为什么要进行SVD分解?他有什么直观的物理或者几何含义?
SVD分解的公式又是如何推导出来的?
四.PCA降维
数据降维是干嘛?为什么能丢掉一些维度,为什么特征值大就是主成分?SVD分解在降维中的应用。
一.线性变换
什么是线性变换?在数学中,线性映射(也叫做线性变换或线性算子)是在两个向量空间之间的函数,它保持向量加法和标量乘法的运算。术语“线性变换”特别常用,尤其是对从向量空间到自身的线性映射。
如果 V 和 W 是有限维的,并且在这些空间中有选择好的基,则从 V 到 W 的所有线性映射可以被表示为矩阵;(来自维基百科)
上面说的这么迷糊,线性变换就是向量加法和标量乘法的运算,而矩阵乘法正好就只有加和乘的运算。
所以这里,我要解释的是线性变换在这种加法和乘法里所带来的拉伸效果或者说是解释向量如何在不同矩阵空间中表示。
这部分首先用两个特例来演示线性变换的拉伸效果(其实也就是一个矩阵左乘一个向量),然后用基底的变换来解释矩阵乘法,以及为什么会产生这种效果。
先通过两个二维的简单特例来图示线性变换的拉伸效果:
1.假设有一个对角矩阵M,M乘以一个向量(x,y)可以看做M将点(x,y)变换为另一个点
变换的效果如下,变换后的平面仅仅是沿 X 水平方面进行了拉伸3倍,垂直方向是并没有发生变化。
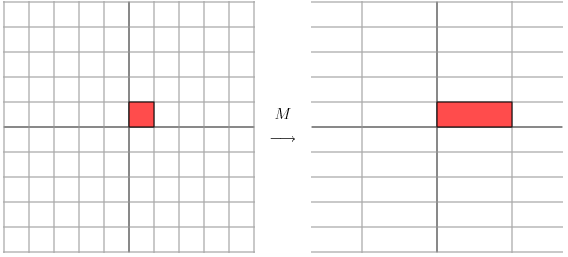
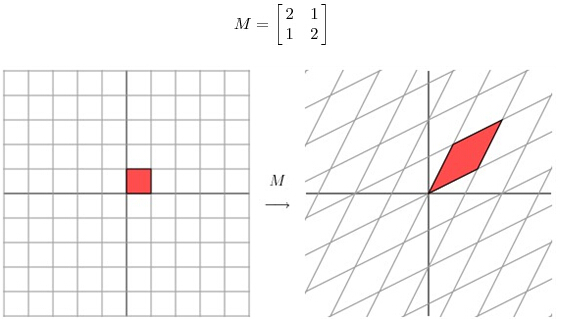
2.看另一个矩阵
用这个矩阵乘以其他向量,产生的效果:
图片来源 http://www.ams.org/samplings/feature-column/fcarc-svd
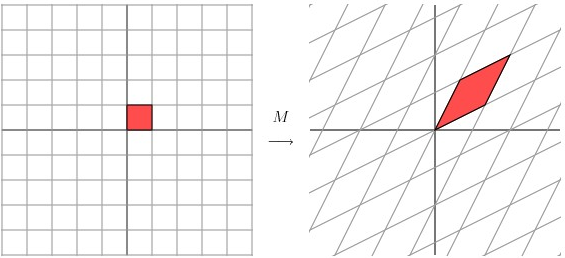
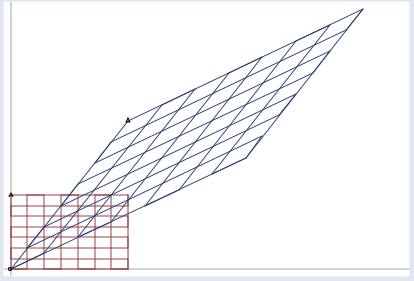
这种效果的另一种演示,请注意基底的变化(即图中矩阵的边界,原来是正交的,变化后不是):
图片来源 http://blog.stata.com/2011/03/03/understanding-matrices-intuitively-part-1/
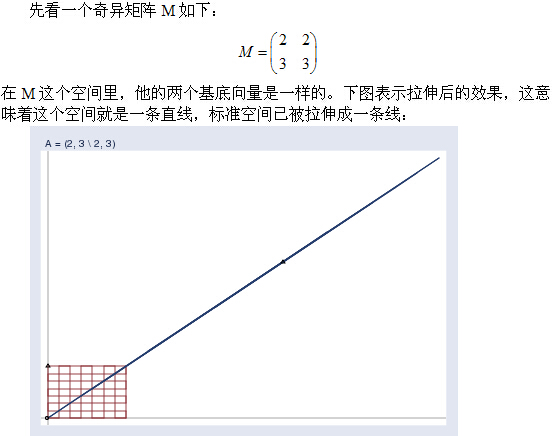
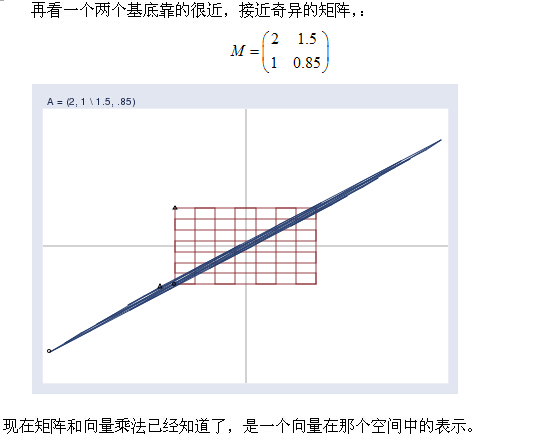
在进行下面的解释之前,我想灌输一个概念,一个矩阵的列向量就是一组“基底"(先不谈奇异矩阵)。这些基底就张成了一个空间。如3阶单位矩阵I,它的列向量就张成了我们熟知的三维坐标系笛卡尔空间。







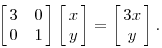
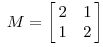






















 1994
1994

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








