在多视角几何中,特别是在一些恢复相机运动轨迹的模型中,我们需要将相机的旋转和平移表示出来。通常情况下,我们都是在欧几里得空间中用R和t来进行相应的运算得到相机轨迹。然而,在很多论文中,作者们却喜欢用Lie algebra se(3)、so(3) 以及 Lie group SE(3)、SO(3) 之类的表示。紧接着,出现了很多术语,比如twist, tangent space,也出现了一些运算,比如exp(),log()之类的,看得我是云里雾里。
比如下面这个公式, 是由三个角速度组成的向量,
表示对应的旋转矩阵,
表示由三个角速度组成的反对称矩阵(skew-symmetric matrix)。
本篇博客将从最基础的内容出发,用直观的容易理解的方式对旋转矩阵和李代数之间的关系进行推导,如有错误,请指出,希望共同进步。
预备知识:
在进入正题之前,我们先需要复习下向量叉积(cross product),以及反对称矩阵(skew symmetric matrix),在计算机视觉中最初遇到这些概念应该是在求解本征矩阵时,然而,他们在沟通刚体变换矩阵和李代数之间扮演着十分重要的作用。
对给定的两个三维实数向量,它们的叉积可以通过下面的公式计算出来:
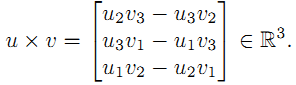
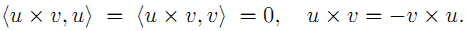
这种两个向量的运算可以通过一个矩阵来表示,即
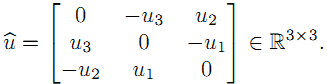
请记住这个性质。并且任意一个3*3的反对称矩阵,我们能够找到一个三维向量和它对应。 至于什么是刚体变换,什么是旋转矩阵,旋转矩阵有哪些性质这些更基础的知识在这里不再一一补充。
下面的内容中,都是基于3维空间,所以没有特别说明时,所说的旋转矩阵都是3*3的,平移向量也是3维的。并且所有向量上带一个帽子的表示的是它的反对称矩阵形式。
旋转矩阵与 so(3):
我们知道对于旋转矩阵,旋转矩阵本身乘以它的转置等于单位矩阵:
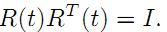
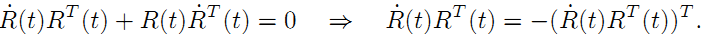 (1)
(1)
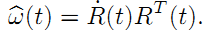 (2)
(2)
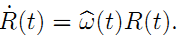 (3)
(3)
在介绍我们期待已久的指数映射前,先挖掘挖掘(3)式的一些含义。如果初始时刻
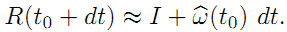
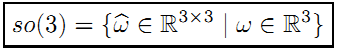
注意是大写: 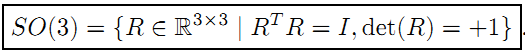
指数映射:
回到公式(3),把旋转矩阵R用x替换掉,如下:
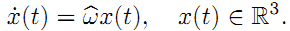
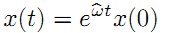
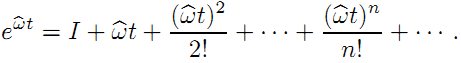 ) (4)
) (4)
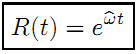 (5)
(5)
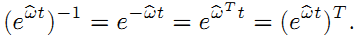


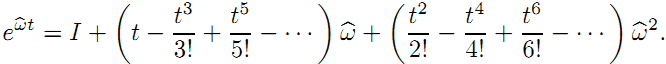


上面推导的是连续时间的,并且假设 ||w||=1 ,即旋转速度为单位速度, t 是一个时间跨度,联合起来的物理意义就是在单位旋转速度
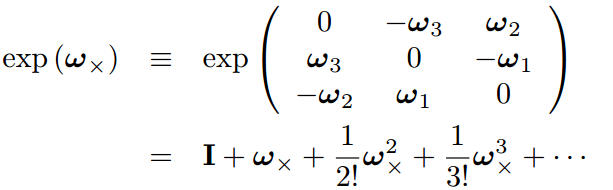
简单整理:
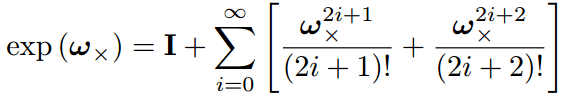

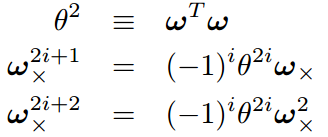
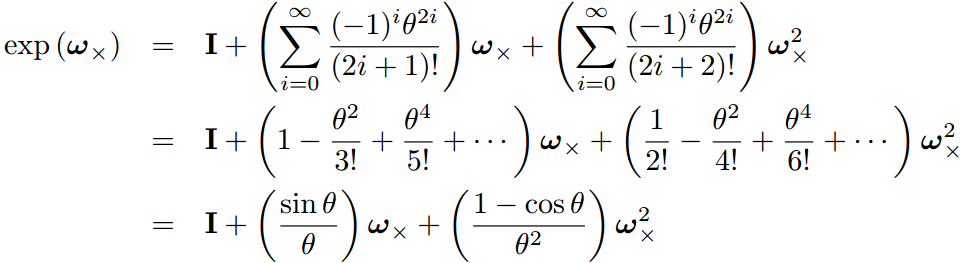
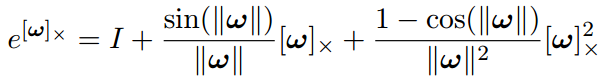
刚体变换和SE(3):
前面还只说了旋转,实际上刚体变换还有平移。所以,和只有旋转矩阵构成的李群SO(3) 一样,我们也可以有由刚体变换得到的李群SE(3) :
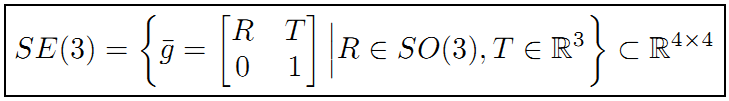
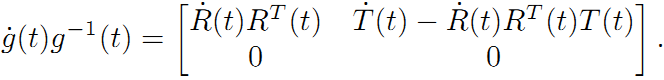
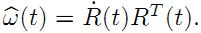
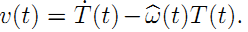
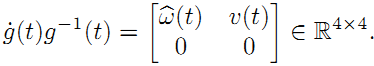
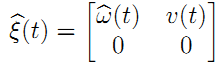
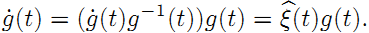
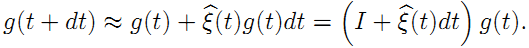
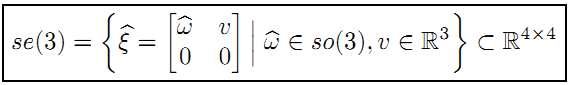
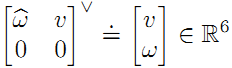

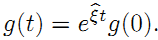
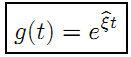
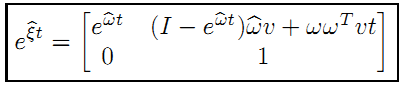
这里也来一个去掉时间t的版本:
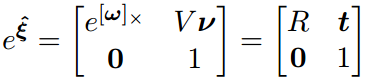
矩阵的各个部分对应如下:
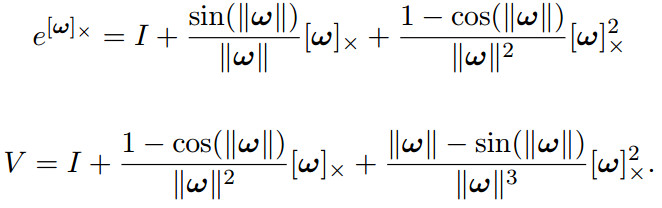
到这里基本理清了SE,SO之类的与刚体变换之间的关系,看视觉SLAM类的论文以及相应代码中有关lie部分应该没啥压力了。
各种论文里涉及到的求解位姿矩阵时的非线性最小二乘优化(牛顿法,LM法),其中增量都是在单位矩阵处的tangent space se(3)上计算,获得的增量(即相邻位姿变换关系)通过指数映射映射回多面体SE(3)上。
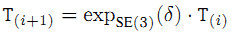
这篇博文可以说是我看慕尼黑工大(TUM)多视角几何教学视频的笔记,YouTube链接点击这里,这位牛的飞老师的英语吐字清晰,大家应该能够听懂。当然,老师也是参看的别人的文档,这里我也把讲lie 和计算机视觉的两个文档传到了csdn上,供大家下载。
祝好
–白巧克力






















 615
615

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








