实验力学应试笔记
实验应力分析基础
电测法
1.概念
惠斯通电桥:由四个电阻组成的电桥电路,利用电阻的变化来测量物理量的变化
温度补偿原因:当环境温度变化时,因应变片的线膨胀系数与被测构件的线膨胀系数不同,且敏感栅的电阻值随温度的变化而变化,所以测得应变将包含温度变化的影响,不能反映构件的实际应变,因此在测量中必须设法消除温度变化的影响
补偿块:补偿块材料与被测构件相同,不受外力,处于同一温度场
补偿片:粘贴在补偿块上,与工作应变片规格相同
常用应变片:阻值 120 Ω,灵敏系数 2
零点漂移原因:
-
敏感栅通工作电流后产生温度效应;
-
在制造与安装中产生的内应力;
-
粘结剂固化不充分;敏感栅材料逐渐氧化;
-
粘结剂、基底材料性能变化
减小误差:对零漂进行定量测定,对应变测量读数进行修正
根据应力状态选择应变片:
-
单向应力
沿主应力方向贴片
-
已知主应力 二向应力
沿两个主应力方向各贴应变片
-
未知主应力方向 二向应力
-
大致知道主应力方向: 4 5 ∘ 45^\circ 45∘ 应变花
-
无法估计主应力方向: 6 0 ∘ 60^\circ 60∘ 应变花
-
灵敏度系数
对于如图所示的全桥
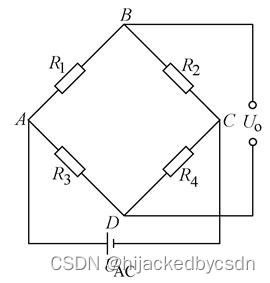
K 仪 ε 仪 = K ( ε 1 − ε 2 − ε 3 + ε 4 ) K_仪\varepsilon_仪 = K(\varepsilon_1 - \varepsilon_2 - \varepsilon_3 + \varepsilon_4) K仪ε仪=K(ε1−ε2−ε3+ε4)
其中, K K K 为应变计的灵敏系数, K 仪 K_仪 K仪 为应变仪的灵敏系数
ε 1 , ε 2 , ε 3 , ε 4 \varepsilon_1, \varepsilon_2, \varepsilon_3, \varepsilon_4 ε1,ε2,ε3,ε4 是 R 1 , R 2 , R 3 , R 4 R_1, R_2, R_3, R_4 R1,R2,R3,R4 应变片的实际应变, ε 仪 \varepsilon_仪 ε仪 是应变仪的读数
若仅有一个桥臂感受电阻变化,则有
d R R = K ε = K 仪 ε 仪 \frac {dR} {R} = K\varepsilon = K_仪\varepsilon_仪 RdR=Kε=K仪ε仪
广义胡克定律
1.简单情况
1.1 轴向拉压变形
σ x = E ε x \sigma_x = E\varepsilon_x σx=Eεx
同时导致横向变形
ε y = − μ ε x = − μ σ x E \varepsilon_y = -\mu\varepsilon_x = -\mu \frac {\sigma_x} {E} εy=−μεx=−μEσx
1.2 纯剪切
τ = G γ \tau = G \gamma τ=Gγ
2.主应力单元体/非主应力单元体
即对于各向同性材料,在小变形及线弹性范围内:
线应变只与正应力有关,而与剪应力无关;
剪应变只与剪应力有关,而与正应力无关;
则由叠加原理,主应力单元体/非主应力单元体的应力状态是轴向拉压变形和纯剪切的叠加:
ε x = 1 E [ σ x − μ ( σ y + σ z ) ] ε y = 1 E [ σ y − μ ( σ z + σ x ) ] ε z = 1 E [ σ z − μ ( σ x + σ y ) ] γ x y = 1 G τ x y γ y z = 1 G τ y z γ z x = 1 G τ z x \begin{align*} \varepsilon_x &= \frac {1} {E} [\sigma_x - \mu(\sigma_y + \sigma_z)] \\ \varepsilon_y &= \frac {1} {E} [\sigma_y - \mu(\sigma_z + \sigma_x)] \\ \varepsilon_z &= \frac {1} {E} [\sigma_z - \mu(\sigma_x + \sigma_y)] \\ \gamma_{xy} &= \frac {1} {G} \tau_{xy} \\ \gamma_{yz} &= \frac {1} {G} \tau_{yz} \\ \gamma_{zx} &= \frac {1} {G} \tau_{zx} \end{align*} εxεyεzγxyγyzγzx=E1[σx−μ(σy+σz)]=E1[σy−μ(σz+σx)]=E1[σz−μ(σx+σy)]=G1τxy=G1τyz=G1τzx
平面应力状态分析
σ α = σ x + σ y 2 + σ x − σ y 2 c o s 2 α − τ x y s i n 2 α τ α = σ x − σ y 2 s i n 2 α − τ x y c o s 2 α \begin{align*} \sigma_\alpha &= \frac {\sigma_x + \sigma_y} {2} + \frac {\sigma_x - \sigma_y} {2} cos{2\alpha} - \tau_{xy} sin{2\alpha} \\ \tau_\alpha &= \frac {\sigma_x - \sigma_y} {2} sin{2\alpha} - \tau_{xy} cos{2\alpha} \end{align*} σατα=2σx+σy+2σx−σycos2α−τxysin2α=2σx−σysin2α−τxycos2α
其中 α \alpha α 为从x轴正方向逆时针转到面的法向的夹角
变形,得到平面应力状态分析公式的物理意义为一个应力圆:
( σ α − σ x + σ y 2 ) 2 + τ α 2 = ( σ x − σ y 2 ) 2 + τ x y 2 (\sigma_\alpha - \frac {\sigma_x + \sigma_y} {2})^2 + \tau_\alpha^2 = (\frac {\sigma_x - \sigma_y} {2})^2 + \tau_{xy}^2 (σα−2σx+σy)2+τα2=(2σx−σy)2+τxy2
应变计的贴法
-
检查和分选应变计
贴片前应对应变计进行外观检查和阻值测量。检查应变计的敏感栅有无锈斑、基底和覆盖层有无破损、引线是否牢固等。阻值测量的目的是检查应变计是否有断路、短路情况,并按阻值进行分选,以保证使用同一温度补偿片的一组应变计的阻值相差不超过 0.1Ω
-
粘贴表面的准备
首先,除去构件粘贴表面的油污、漆、锈斑、电镀层等,用砂布交叉打磨出细纹以增加粘结力,接着用浸有酒精(或丙酮)的纱布片或脱脂棉球擦洗,并用钢画针画出贴片定位线。最后,再进行一次擦洗,直至纱布片或棉球上不见污迹为止
-
贴片
在应变计的底面和处理过的粘贴表面上,各涂一层薄而均匀的胶,用镊子将应变计放上并调好位置,然后盖上氟塑料薄膜,用手指揉和滚压,挤出多余的胶,并排除应变计下面的气泡,使应变计和试件完全贴合。过适当时间后,从应变计无引线的一端开始向有引线的一端揭掉氟塑料薄膜,用力方向尽量与粘结表面平行
-
固化
贴片时最常用的是氰基丙稀酸酯粘结剂(如 502 胶水、501 胶水粘结剂)。用它贴片后,只要在室温下放置数小时即可充分固化,而具有较强的粘结能力。对于需要加温固化的粘结剂,应严格按规范进行。一般是用红外线灯烘烤,但加温速度不能太快,以免产生气泡
-
测量导线的焊接与固定
待粘结剂初步固化以后,即可焊接导线。常温静态应变测量时,导线可采用 ϕ0.1~ϕ0.3mm 的单丝纱包铜线或多股铜芯塑料软线
导线与应变计引线之间连接最好使用接线端子片,如图 1 所示

-
检查
对已充分固化并已接好导线的应变计,在正式使用前必须进行质量检查。除对应变计作外观检查外,还应检查应变计是否粘贴良好、贴片方位是否正确、有无短路和断路、绝缘电阻是否符合要求(一般不低于100MΩ)等
测量电桥原理
电桥输入恒定时,输出电压与桥臂电阻变化率之间的关系:
U o = U A B 4 ( Δ R 1 R 1 − Δ R 2 R 2 − Δ R 3 R 3 + Δ R 4 R 4 ) / [ 1 + 1 2 ( Δ R 1 R 1 + Δ R 2 R 2 + Δ R 3 R 3 + Δ R 4 R 4 ) ] U_o = \frac {U_AB} {4} (\frac {\Delta R_1} {R_1} - \frac {\Delta R_2} {R_2} - \frac {\Delta R_3} {R_3} + \frac {\Delta R_4} {R_4})/[1+\frac {1} {2} (\frac {\Delta R_1} {R_1} + \frac {\Delta R_2} {R_2} + \frac {\Delta R_3} {R_3} + \frac {\Delta R_4} {R_4})] Uo=4UAB(R1ΔR1−R2ΔR2−R3ΔR3+R4ΔR4)/[1+21(R1ΔR1+R2ΔR2+R3ΔR3+R4ΔR4)]
应变计的电阻变化率 Δ R R \frac {\Delta R} {R} RΔR 一般远小于 1,因此可以略去上式分母中的电阻变化率,得到输出电压与桥臂电阻变化率之间的线性关系:
U o = U A B 4 ( Δ R 1 R 1 − Δ R 2 R 2 − Δ R 3 R 3 + Δ R 4 R 4 ) U_o = \frac {U_AB} {4} (\frac {\Delta R_1} {R_1} - \frac {\Delta R_2} {R_2} - \frac {\Delta R_3} {R_3} + \frac {\Delta R_4} {R_4}) Uo=4UAB(R1ΔR1−R2ΔR2−R3ΔR3+R4ΔR4)
由于略去电阻变化率产生的非线性相对误差:
e = a b s 1 2 ( Δ R 1 R 1 + Δ R 2 R 2 + Δ R 3 R 3 + Δ R 4 R 4 ) e=abs{\frac {1} {2} (\frac {\Delta R_1} {R_1} + \frac {\Delta R_2} {R_2} + \frac {\Delta R_3} {R_3} + \frac {\Delta R_4} {R_4})} e=abs21(R1ΔR1+R2ΔR2+R3ΔR3+R4ΔR4)
应变计的应变变化与电阻应变率的关系:
Δ R R = K ε \frac {\Delta R} {R} = K \varepsilon RΔR=Kε
其中, K 为应变计的灵敏系数
代入输出电压与桥臂电阻变化率之间的线性关系,得输出电压与应变片粘贴点的应变之间的线性关系:
U o = U A B 4 ( ε 1 − ε 2 − ε 3 + ε 4 ) U_o=\frac {U_AB} {4} (\varepsilon_1-\varepsilon_2-\varepsilon_3+\varepsilon_4) Uo=4UAB(ε1−ε2−ε3+ε4)
同理得上式的非线性相对误差:
e = a b s 1 2 ( ε 1 + ε 2 + ε 3 + ε 4 ) e = abs{\frac {1} {2}(\varepsilon_1+\varepsilon_2+\varepsilon_3+\varepsilon_4)} e=abs21(ε1+ε2+ε3+ε4)
电阻应变计在电桥中的接线方法
记应变仪的读数为:
ε d = ε 1 − ε 2 − ε 3 + ε 4 \varepsilon_d = \varepsilon_1 - \varepsilon_2 - \varepsilon_3 + \varepsilon_4 εd=ε1−ε2−ε3+ε4
固定电阻受温度和工作环境的影响很小,即 ,相应地有 。
电桥相对两臂接工作应变计,另相对两臂接温度补偿应变计,则有:
ε 1 = ε 1 ′ + ε t ε 2 = ε t ε 3 = ε t ε 4 = ε 4 ′ + ε t \begin{align*} \varepsilon_1 &= \varepsilon'_1 + \varepsilon_t \\ \varepsilon_2 &= \varepsilon_t \\ \varepsilon_3 &= \varepsilon_t \\ \varepsilon_4 &= \varepsilon'_4 + \varepsilon_t \end{align*} ε1ε2ε3ε4=ε1′+εt=εt=εt=ε4′+εt
应变仪的读数应为:
ε d = ε 1 ′ + ε 4 ′ \varepsilon_d = \varepsilon'_1 + \varepsilon'_4 εd=ε1′+ε4′
串联和并联式接线法:

1.串联接线法
-
串联接线后桥臂的应变为各个应变计应变值的算术平均值
-
当每一桥臂中串联的各个应变计的应变相同时,即ε=ε=…=ε=ε′时,则
-
串联后的桥臂电阻增大,在限定电流下,可以提高供桥电压,相应地使读数应变增大
2.并联接线法
<img src = “https://img-blog.csdnimg.cn/d61a48708e3040be94a699c31997f978.png” height = 350
-
并联接线后桥臂的应变为各个应变计应变值的算术平均值
-
当同一桥臂中并联的所有应变计的电阻改变量都相同时,即ΔR=ΔR=…=ΔR=ΔR′,各个应变计的应变也均相同,设为ε′,则桥臂的应变为
-
并联后的桥臂电阻减小,在通过应变计的电流不超过最大工作电流的条件下,电桥的输出电流可以相应地提高n倍,这对于直接用电流表或记录仪器是有利的
测量电桥的应用
1.半桥接线法的应用
2.全桥接线法的应用
半桥接线法的应用
1.拉压应变的测量
2.扭转切应力的测量
3.弯曲应变的测量
4.弯曲切应力的测量
5.拉弯组合变形时的应变测量
拉压应变的测量

1.单臂测量
R 1 R_1 R1 沿构件轴向粘贴在构件表面 应力状态为轴向拉压变形
R 2 R_2 R2 粘贴在补偿块上
R 3 R_3 R3、 R 4 R_4 R4 为固定电阻
ε 1 = ε F + ε t ε 2 = ε t ε 3 = 0 ε 4 = 0 \begin{align*} \varepsilon_1 &= \varepsilon_F + \varepsilon_t \\ \varepsilon_2 &= \varepsilon_t \\ \varepsilon_3 &= 0 \\ \varepsilon_4 &= 0 \end{align*} ε1ε2ε3ε4=εF+εt=εt=0=0
应变仪的读数应为:
ε d = ε F \varepsilon_d = \varepsilon_F εd=εF
2.半桥测量
R 1 R_1 R1 沿构件轴向粘贴在构件表面 应力状态为轴向拉压变形
R 2 R_2 R2 沿构件横向粘贴在构件表面 应力状态为轴向拉压变形下的横向变形
R 3 R_3 R3、 R 4 R_4 R4 为固定电阻
ε 1 = ε F + ε t ε 2 = − μ ε F + ε t ε 3 = 0 ε 4 = 0 \begin{align*} \varepsilon_1 &= \varepsilon_F + \varepsilon_t \\ \varepsilon_2 &= -\mu \varepsilon_F + \varepsilon_t \\ \varepsilon_3 &= 0 \\ \varepsilon_4 &= 0 \end{align*} ε1ε2ε3ε4=εF+εt=−μεF+εt=0=0
应变仪的读数应为:
ε d = ( 1 + μ ) ε F \varepsilon_d = (1+\mu)\varepsilon_F εd=(1+μ)εF
扭转切应力的测量

由于圆轴表面上任一点为纯剪切应力状态,所以对于任一一点都有
σ 0 ∘ = σ x = 0 σ 9 0 ∘ = σ y = 0 τ x y = τ \begin{align*} \sigma_{0^\circ} &= \sigma_x = 0 \\ \sigma_{90^\circ} &= \sigma_y = 0 \\ \tau_{xy} &= \tau \end{align*} σ0∘σ90∘τxy=σx=0=σy=0=τ
在平面应力状态分析公式中代入 α = − 4 5 ∘ , 4 5 ∘ \alpha = -45^\circ, 45^\circ α=−45∘,45∘ 得
σ − 4 5 ∘ = τ x y = τ τ − 4 5 ∘ = 0 σ 4 5 ∘ = − τ x y = − τ τ 4 5 ∘ = 0 \begin{align*} \sigma_{-45^\circ} &= \tau_{xy} = \tau \\ \tau_{-45^\circ} &= 0 \\ \sigma_{45^\circ} &= -\tau_{xy} = -\tau \\ \tau_{45^\circ} &= 0 \end{align*} σ−45∘τ−45∘σ45∘τ45∘=τxy=τ=0=−τxy=−τ=0
R 1 R_1 R1 与构件轴向成 -45 度粘贴在构件表面 应力状态为纯剪切 对应 σ − 4 5 ∘ \sigma_{-45^\circ} σ−45∘
R 2 R_2 R2 沿构件横向成 45 度粘贴在构件表面 应力状态为纯剪切 对应 σ 4 5 ∘ \sigma_{45^\circ} σ45∘
R 3 R_3 R3、 R 4 R_4 R4 为固定电阻
ε 1 = ε n + ε t ε 2 = − ε n + ε t ε 3 = 0 ε 4 = 0 \begin{align*} \varepsilon_1 &= \varepsilon_n + \varepsilon_t \\ \varepsilon_2 &= -\varepsilon_n + \varepsilon_t \\ \varepsilon_3 &= 0 \\ \varepsilon_4 &= 0 \end{align*} ε1ε2ε3ε4=εn+εt=−εn+εt=0=0
应变仪的读数应为:
ε d = 2 ε n \varepsilon_d = 2\varepsilon_n εd=2εn
由广义胡克定律:
ε x = 1 E [ σ x − μ ( σ y + σ z ) ] \varepsilon_x = \frac {1} {E} [\sigma_x - \mu(\sigma_y + \sigma_z)] εx=E1[σx−μ(σy+σz)]
得:
ε n = 1 E [ σ − 4 5 ∘ − μ ( σ 4 5 ∘ + 0 ) ] \varepsilon_n = \frac {1} {E} [\sigma_{-45^\circ} - \mu(\sigma_{45^\circ} + 0)] εn=E1[σ−45∘−μ(σ45∘+0)]
代入 σ − 4 5 ∘ , σ 4 5 ∘ \sigma_{-45^\circ},\sigma_{45^\circ} σ−45∘,σ45∘ 得:
ε n = 1 E ( 1 + μ ) τ = τ 2 G = γ 2 \varepsilon_n = \frac {1} {E}(1+\mu)\tau = \frac {\tau} {2G} = \frac {\gamma} {2} εn=E1(1+μ)τ=2Gτ=2γ
代入 ε n = 1 2 ε d \varepsilon_n = \frac {1} {2} \varepsilon_d εn=21εd,既可测切应力,也可以测剪切模量:
τ = G ε d \tau = G\varepsilon_d τ=Gεd
γ = ε d \gamma = \varepsilon_d γ=εd
实际加载时:
G = τ γ = T W ε d G = \frac {\tau} {\gamma} = \frac {T} {W\varepsilon_d} G=γτ=WεdT
其中 W 为抗扭截面模量
弯曲应变的测量

R 1 R_1 R1 粘贴在构件上表面 应力状态为轴向拉压变形 拉
R 2 R_2 R2 粘贴在构件下表面 应力状态为轴向拉压变形 压
R 3 R_3 R3、 R 4 R_4 R4 为固定电阻
ε 1 = ε v + ε t ε 2 = − ε v + ε t ε 3 = 0 ε 4 = 0 \begin{align*} \varepsilon_1 &= \varepsilon_v + \varepsilon_t \\ \varepsilon_2 &= -\varepsilon_v + \varepsilon_t \\ \varepsilon_3 &= 0 \\ \varepsilon_4 &= 0 \end{align*} ε1ε2ε3ε4=εv+εt=−εv+εt=0=0
应变仪的读数应为:
ε d = 2 ε v \varepsilon_d = 2\varepsilon_v εd=2εv
弯曲切应力的测量

中性层上各点为纯切应力状态
与圆轴的扭转切应力的测量相似
拉弯组合变形时的应变测量
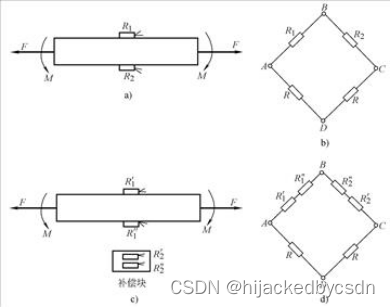
R 1 , R 1 ′ R_1,R'_1 R1,R1′ 粘贴在构件上表面 应力状态为轴向拉压变形 F拉 M 拉
R 2 , R 1 ′ ′ R_2,R''_1 R2,R1′′ 粘贴在构件下表面 应力状态为轴向拉压变形 F拉 M 压
R 2 ′ , R 2 ′ ′ R'_2,R''_2 R2′,R2′′ 粘贴在补偿块上
R 3 R_3 R3、 R 4 R_4 R4 为固定电阻
ε 1 = ε 1 ′ = ε F + ε M + ε t ε 2 = ε 1 ′ ′ = ε F − ε M + ε t ε 2 ′ = ε 2 ′ ′ = ε t ε 3 = 0 ε 4 = 0 \begin{align*} \varepsilon_1 &= \varepsilon'_1 = \varepsilon_F + \varepsilon_M + \varepsilon_t \\ \varepsilon_2 &= \varepsilon''_1 = \varepsilon_F - \varepsilon_M + \varepsilon_t \\ \varepsilon_2' &= \varepsilon_2'' = \varepsilon_t \\ \varepsilon_3 &= 0 \\ \varepsilon_4 &= 0 \end{align*} ε1ε2ε2′ε3ε4=ε1′=εF+εM+εt=ε1′′=εF−εM+εt=ε2′′=εt=0=0
对于 R 1 , R 2 , R , R R_1,R_2,R,R R1,R2,R,R 组桥,应变仪的读数应为:
ε d = ( ε F + ε M + ε t ) − ( ε F − ε M + ε t ) + 0 − 0 = 2 ε M \begin{align*} \varepsilon_d &= (\varepsilon_F + \varepsilon_M + \varepsilon_t) - (\varepsilon_F - \varepsilon_M + \varepsilon_t) + 0 - 0 \\ {} &= 2\varepsilon_M \end{align*} εd=(εF+εM+εt)−(εF−εM+εt)+0−0=2εM
对于 R 1 ′ , R 1 ′ ′ , R 2 ′ , R 2 ′ ′ , R , R R'_1,R''_1,R'_2,R''_2,R,R R1′,R1′′,R2′,R2′′,R,R 组桥,应变仪的读数应为:
ε d = ( ε F + ε M + ε t ) + ( ε F − ε M + ε t ) − ε t − ε t + 0 − 0 = 2 ε F \begin{align*} \varepsilon_d &= (\varepsilon_F + \varepsilon_M + \varepsilon_t) + (\varepsilon_F - \varepsilon_M + \varepsilon_t) - \varepsilon_t - \varepsilon_t + 0 - 0 \\ {} &= 2\varepsilon_F \end{align*} εd=(εF+εM+εt)+(εF−εM+εt)−εt−εt+0−0=2εF
全桥接线法的应用
1.拉弯扭组合变形时的扭转切应力测量
2.材料弹性模量 E 和泊松比 μ 的测量
拉弯扭组合变形时的扭转切应力测量

R 2 , R 4 R_2,R_4 R2,R4 与构件轴向成 45 度粘贴在构件中性面 应力状态为轴向拉压变形+纯剪 无弯矩影响
R 1 , R 3 R_1,R_3 R1,R3 与构件轴向成 -45 度粘贴在构件中性面 应力状态为轴向拉压变形+纯剪 无弯矩影响
ε 1 = ε F + 0 + ε n + ε t ε 2 = ε F − 0 − ε n + ε t ε 3 = ε F + 0 − ε n + ε t ε 4 = ε F − 0 + ε n + ε t \begin{align*} \varepsilon_1 &= \varepsilon_F + 0 + \varepsilon_n + \varepsilon_t \\ \varepsilon_2 &= \varepsilon_F - 0 - \varepsilon_n + \varepsilon_t \\ \varepsilon_3 &= \varepsilon_F + 0 - \varepsilon_n + \varepsilon_t \\ \varepsilon_4 &= \varepsilon_F - 0 + \varepsilon_n + \varepsilon_t \end{align*} ε1ε2ε3ε4=εF+0+εn+εt=εF−0−εn+εt=εF+0−εn+εt=εF−0+εn+εt
应变仪的读数应为:
ε d = 4 ε n \varepsilon_d = 4\varepsilon_n εd=4εn
材料弹性模量E和泊松比μ的测量

R 1 R_1 R1 沿构件轴向粘贴在构件上表面 应力状态为轴向拉压变形
R 1 ′ R'_1 R1′ 沿构件横向粘贴在构件上表面 应力状态为轴向拉压变形下的横向变形
R 4 R_4 R4 沿构件轴向粘贴在构件上表面 应力状态为轴向拉压变形
R 1 ′ R'_1 R1′ 沿构件横向粘贴在构件上表面 应力状态为轴向拉压变形下的横向变形
R 2 , R 2 ′ , R 3 , R 3 ′ R_2,R'_2,R_3,R'_3 R2,R2′,R3,R3′ 粘贴在补偿片上
ε 1 = ε 4 = ε F + ε t ε 1 ′ = ε 4 ′ = − μ ε F + ε t ε 2 = ε 2 ′ = ε 3 = ε 3 ′ = ε t \begin{align*} \varepsilon_1 &= \varepsilon_4 = \varepsilon_F + \varepsilon_t \\ \varepsilon'_1 &= \varepsilon'_4 = -\mu \varepsilon_F + \varepsilon_t \\ \varepsilon_2 &= \varepsilon'_2 = \varepsilon_3 = \varepsilon'_3 = \varepsilon_t \end{align*} ε1ε1′ε2=ε4=εF+εt=ε4′=−μεF+εt=ε2′=ε3=ε3′=εt
R 1 , R 2 , R 3 , R 4 R_1,R_2,R_3,R_4 R1,R2,R3,R4 组桥,应变仪的读数应为:
ε d = ε F + ε t − ε t − ε t + ε F + ε t = 2 ε F \begin{align*} \varepsilon_d &= \varepsilon_F + \varepsilon_t - \varepsilon_t - \varepsilon_t + \varepsilon_F + \varepsilon_t \\ {} &= 2\varepsilon_F \end{align*} εd=εF+εt−εt−εt+εF+εt=2εF
R 1 ′ , R 2 ′ , R 3 ′ , R 4 ′ R'_1,R'_2,R'_3,R'_4 R1′,R2′,R3′,R4′ 组桥,应变仪的读数应为:
ε d = ( − μ ε F + ε t ) − ε t − ε t + ( − μ ε F + ε t ) = − 2 μ ε F \begin{align*} \varepsilon_d &= (-\mu \varepsilon_F + \varepsilon_t) - \varepsilon_t - \varepsilon_t + (-\mu \varepsilon_F + \varepsilon_t) \\ {} &= -2\mu \varepsilon_F \end{align*} εd=(−μεF+εt)−εt−εt+(−μεF+εt)=−2μεF
偏心拉伸
偏心拉伸试样包含两个方面的内力
1.拉伸
σ F = E ε F σ F = F A = F b h \begin{align*} \sigma_F &= E\varepsilon_F \\ \sigma_F &= \frac {F} {A} = \frac {F} {bh} \end{align*} σFσF=EεF=AF=bhF
其中 E 为弹性模量,F 为拉伸载荷
b 为截面沿 z 轴方向的边的长度,h 为截面沿 y 轴方向的边的长度
2.弯曲

弯应力沿厚度方向线性分布:
σ M = M I z y = F e I z y = 12 F e b h 3 y \sigma_M = \frac {M} {I_z} y = \frac {Fe} {I_z} y = \frac {12Fe} {bh^3} y σM=IzMy=IzFey=bh312Fey
b 为截面沿 z 轴方向的边的长度,h 为截面沿 y 轴方向的边的长度
在弯曲应力最大值的地方 y = h/2:
σ M = E ε M σ M = M W z = F e W z = 6 F e b h 2 \begin{align*} \sigma_M &= E\varepsilon_M \\ \sigma_M &= \frac {M} {W_z} = \frac {Fe} {W_z} = \frac {6Fe} {bh^2} \end{align*} σMσM=EεM=WzM=WzFe=bh26Fe
其中 Wz 为抗弯截面模量,e 为偏心矩
有些地方把截面描述为 t 为试样截面的长边长度,b 为试样截面的短边长度
然后记 W_z = tb^2/6
个人感觉这样不是很好……因为忽略了截面中的 z 轴和 y 轴的位置
光弹性法
光波的正弦表达式
u = a s i n ( ω t + φ ) u = asin(\omega t + \varphi) u=asin(ωt+φ)
其中 a a a 为振幅
ω \omega ω 为圆频率
φ \varphi φ 为相位
代入 ω = 2 π λ ν \omega = \frac {2 \pi} {\lambda} \nu ω=λ2πν, φ = 2 π λ x \varphi = \frac {2 \pi} {\lambda} x φ=λ2πx,得
u = a s i n 2 π λ ( ν t + x ) u = asin\frac {2 \pi} {\lambda}(\nu t + x) u=asinλ2π(νt+x)
其中 λ \lambda λ 为波长
ν \nu ν 为速度
x x x 为光程
相位差与光程差之间的关系
相位差
δ = 2 π λ ( ν t + x 1 ) − 2 π λ ( ν t + x 2 ) = 2 π λ ( x 1 − x 2 ) \delta = \frac {2 \pi} {\lambda}(\nu t + x_1) - \frac {2 \pi} {\lambda}(\nu t + x_2) = \frac {2 \pi} {\lambda}(x_1 - x_2) δ=λ2π(νt+x1)−λ2π(νt+x2)=λ2π(x1−x2)
光程差
Δ = x 1 − x 2 \Delta = x_1 - x_2 Δ=x1−x2
相位差与光程差之间的关系
δ = 2 π λ Δ \delta = \frac {2 \pi} {\lambda} \Delta δ=λ2πΔ
3.光强
I = k a 2 I = ka^2 I=ka2
光强与振幅的平方成正比
光弹性实验装置
白光:多种有色光(多个波长)的混合光
单色光:单一波长的光
自然光:横波,沿任意方向振动
平面偏振光:光的横向振动在一个平面内
圆偏振光:以圆轨迹运动的偏振光
光轴:在晶体中的一个特殊的方向,沿该方向不会产生双折射现象
光的双折射现象:指一束光波以入射角为 i 的方向入射时,在进入具有各向异性的晶体以后,光在其中沿各个方向的折射率不同,因而传播速度不同,导致光线将分成两束以不同折射角 φ 1 \varphi_1 φ1, φ 2 \varphi_2 φ2 方向传播,这两束传播方向不同的光波不仅具有不同的传播速度,而且具有不同的偏振方向——它们的偏振方向相互垂直
人工双折射:玻璃、塑料、环氧树脂等各向同性透明非晶体材料,自然状态下通常不产生双折射现象,但当有载荷作用时,其内部会产生应力分布,导致材料由原先的光学各向同性变为各向异性,出现类似晶体的双折射性质
起偏镜:将入射光转化为平面偏振光
四分之一波片:由于四分之一波长相当于二分之派的相位,入射的平面偏振光发生双折射转化为圆偏振光
检偏镜:取入射的圆偏振光在该镜偏振方向上的分量
暗场:当起偏轴和检偏轴正交时,平面偏振光被检偏镜挡住吸收,形成暗场
亮场:当起偏轴和检偏轴平行时,平面偏振光穿过检偏轴,形成亮场

应力-光学定律
应力-光学定律的形式 1 通用
Δ = C h ( σ 1 − σ 2 ) \Delta = Ch(\sigma_1 - \sigma_2) Δ=Ch(σ1−σ2)
Δ \Delta Δ 为光程差 单位 m
C C C 为模型材料的应力光学系数
h h h 为模型厚度
σ \sigma σ 为应力 单位 Pa
意义:当模型厚度 h 一定时,任一点光程差与该点的主应力差成正比
1.平面偏振场


对于正交平面偏振光场,分析可得:
I = k ( a s i n 2 φ s i n δ 2 ) 2 I = k(asin2\varphi sin{\frac{\delta}{2}})^2 I=k(asin2φsin2δ)2
代入相位差与光程差之间的关系 δ = 2 π λ Δ \delta = \frac {2 \pi} {\lambda} \Delta δ=λ2πΔ,得
I = k ( a s i n 2 φ s i n π Δ λ ) 2 I = k(asin2\varphi sin{\frac {\pi \Delta} {\lambda}})^2 I=k(asin2φsinλπΔ)2
可见,
-
光强与光程差 Δ \Delta Δ 有关
-
光强与主应力与起偏镜之间的夹角 φ \varphi φ 有关
研究 I = 0 I = 0 I=0:
-
s i n 2 φ = 0 = > φ = 0 , π / 2 sin2\varphi = 0 => \varphi = 0, \pi /2 sin2φ=0=>φ=0,π/2
-
φ = 0 \varphi = 0 φ=0 时, σ 1 \sigma_1 σ1 与起偏镜的偏振方向重合
-
φ = π / 2 \varphi = \pi /2 φ=π/2 时, σ 2 \sigma_2 σ2 与起偏镜的偏振方向重合
等倾线:模型上应力主轴与起偏镜偏振轴重合的诸点,在检偏镜之后,光均将消失而呈现为黑点,这些点的迹线形成干涉条纹,成为等倾线
等倾线是具有相同主应力方向的点的轨迹,或者说等倾线上各点的主应力方向相同,且为偏振轴的方向
同步转动起偏镜和检偏镜,可以得到不同方向的等倾线
-
-
s i n π Δ λ = 0 = > π Δ λ = N π = > Δ = N λ , N = 0 , 1 , 2... sin{\frac {\pi \Delta} {\lambda}} = 0 => \frac {\pi \Delta} {\lambda} = N \pi => \Delta = N \lambda, N = 0, 1, 2... sinλπΔ=0=>λπΔ=Nπ=>Δ=Nλ,N=0,1,2...
光程差 Δ \Delta Δ 为入射的单色光的波长的整数倍时,在检偏镜之后,光均将消失而呈现为黑点,相同整数倍波长的点的迹线形成干涉条纹,成为等差线
在应力-光学定律的形式 1: Δ = C h ( σ 1 − σ 2 ) \Delta = Ch(\sigma_1 - \sigma_2) Δ=Ch(σ1−σ2) 中代入 Δ = N λ \Delta = N \lambda Δ=Nλ
得 C h ( σ 1 − σ 2 ) = N λ = > σ 1 − σ 2 = N λ C h = f N h Ch(\sigma_1 - \sigma_2) = N \lambda => \sigma_1 - \sigma_2 = \frac {N \lambda} {Ch} = f \frac {N} {h} Ch(σ1−σ2)=Nλ=>σ1−σ2=ChNλ=fhN
得应力-光学定律的形式 2:(只适用于等差线)
σ 1 − σ 2 = f N h \sigma_1 - \sigma_2 = f \frac {N} {h} σ1−σ2=fhN
其中 f = λ C f = \frac {\lambda}{C} f=Cλ 为材料条纹值,是与光源和材料有关的常数,物理意义为产生一级等差线所需的主应力差值
在单色光下,等倾线和等差线均为黑色条纹,如何将它们分开
-
加四分之一波片
-
同步转动起偏镜和检偏镜,等倾线会转动,等差线不动
正常的分析是
平面偏振场 亮场暗场
平面圆偏振场 亮场暗场
现在的情况是,ppt 里面只有平面偏振场的暗场分析
我也懒得自己写hhh
2.平面圆偏振场

光强:
-
暗场 I = k ( a s i n π Δ λ ) 2 I = k(asin{\frac {\pi \Delta} {\lambda}})^2 I=k(asinλπΔ)2
要令 I = 0 I = 0 I=0,有 s i n π Δ λ = 0 = > π Δ λ = N π = > Δ = N λ , N = 0 , 1 , 2... sin{\frac {\pi \Delta} {\lambda}} = 0 => \frac {\pi \Delta} {\lambda} = N \pi => \Delta = N \lambda, N = 0, 1, 2... sinλπΔ=0=>λπΔ=Nπ=>Δ=Nλ,N=0,1,2...
与 φ \varphi φ 无关,所以没有等倾线
与 λ \lambda λ 有关,所以有等差线,出现在光程差等于偶数倍的入射光的波长的点
-
亮场 I = k ( a c o s π Δ λ ) 2 I = k(acos{\frac {\pi \Delta} {\lambda}})^2 I=k(acosλπΔ)2
要令 I = 0 I = 0 I=0,有 c o s π Δ λ = 0 = > π Δ λ = m π 2 = > Δ = m 2 λ , m = 1 , 3 , 5... cos{\frac {\pi \Delta} {\lambda}} = 0 => \frac {\pi \Delta} {\lambda} = m \frac {\pi}{2} => \Delta = \frac {m}{2} \lambda, m = 1, 3, 5... cosλπΔ=0=>λπΔ=m2π=>Δ=2mλ,m=1,3,5...
与 φ \varphi φ 无关,所以没有等倾线
与 λ \lambda λ 有关,所以有等差线,出现在光程差等于奇数倍的入射光的半波长的点
综上,观察两种干涉条纹的实验条件为:
-
等倾线 正交平面偏振光场 白光光源
-
等差线 正交圆偏振光场 白光光源
白色光光源的等差线
以暗场为例,若以白光入射,则某点光程差等于某一色光的波长的整数倍时,该色光被消除,显示出该色光的互补色
因此光程差相同的点显示出相同颜色的条纹
光程差逐渐增大,消光的波长逐渐增大,从紫光到红光,直到等于紫光的新一级整数倍时,进入下一轮循环
亮场则为奇数倍半波长时消光
级数条纹 N 的确定
1.零级条纹
各向同性点:N = 0,光程差 Δ \Delta Δ = 0
根据应力-光学定律的形式 1: Δ = C h ( σ 1 − σ 2 ) \Delta = Ch(\sigma_1 - \sigma_2) Δ=Ch(σ1−σ2)
各向同性点 Δ = 0 = > σ 1 − σ 2 = 0 \Delta = 0 => \sigma_1 - \sigma_2 = 0 Δ=0=>σ1−σ2=0 为模型上主应力差为 0 的点
1)永久性黑色条纹是零级条纹
永久性黑色条纹:即无论载荷增加或减少,零级条纹的位置是不变的
暂时性黑点:当外载荷增加或减少时,这些点时而变黑、时而变亮,因而称为暂时性黑点
暂时性黑点并非真的零级条纹,而是高条纹点
隐没点:该点附近的条纹级数比附近区域的级数都低
发源点:该点附近的条纹级数比附近区域的级数都高
2)模型上的自由方角均为零级条纹
“自由”代表垂直于边界的方向上的应力为 0
“自由方角”进一步代表该点在两个相互垂直的方向的应力为 0
即 σ x , σ y = 0 \sigma_x, \sigma_y = 0 σx,σy=0
又因为自由表面上 τ x y = 0 \tau_{xy} = 0 τxy=0
由平面应力分析公式得,应力圆的圆心和半径都为 0,因此该点在每个方向上的应力都为 0,也即主应力 = 0
故 σ 1 − σ 2 = 0 \sigma_1 - \sigma_2 = 0 σ1−σ2=0
3)拉、压应力的交界处(过渡区)必有零级条纹
因各纵向纤维之间无挤压,所以各点均为单向应力状态
2.色序
以暗场为例,光程差增加时,与自然光波长的关系是:
黑色 0 ->
黄 -> 红 -> 蓝 -> 绿 的波长的一倍 ->
黄 -> 红 -> 蓝 -> 绿 的波长的两倍 -> …
所以沿着条纹级数增加的方向,颜色的变化是循环的
所以两条等色线之间必有一条整数级条纹
亮场则为两条等色线之间必有一条奇数倍半波长条纹
3.不同级数的等色线不会相交,反之,相交的条纹级数必相等
4.在白光下判断条纹级数,在单色光下进行拍照

图 圆盘圆环对径受压的等差线
白光下,干涉条纹具有不同颜色,方便根据色序判断条纹级数
在单色光下,只有某点的光程差等于整数倍的入射光的波长/奇数倍的入射光的半波长时,才会消去该色光
因此等差线是黑色的,等差线以外的区域反射入射光,显示入射光的颜色
这样更容易确定等差线的详细位置
5.在实验时若找不到各向同性点,如何确定其他条纹的级数?
1)连续加载法
一边加载一边观察
最先出现的条纹为第一级条纹
随后出现的条纹级数增大
2)柯可补偿法
非整数级/半整数级条纹的确定
两级条纹之间的级数与距离的关系往往不是线性的,不能直接线性插值
1.旋转检偏镜法
以暗场为例
-
确定模型上待测点的位置
-
设置正交平面偏振光场,同步调整起偏镜和检偏镜,直到某一等倾线通过待测点。由等倾线的角度确定待测点的主应力方向
-
保持起偏镜不动,加入四分之一波片,设置正交圆偏振光场,单独旋转检偏镜,使被测点附近的 N 级和 N -1 级等差线通过该点
第 N 级等差线通过该点时,向被测点转过 θ 1 \theta_1 θ1
N 0 = N − θ 1 / π N_0 = N - \theta_1/\pi N0=N−θ1/π
第 N - 1 级等差线通过该点时,向被测点转过 t h e t a 2 theta_2 theta2
N 0 = ( N − 1 ) + θ 2 / π N_0 = (N-1) + \theta_2/\pi N0=(N−1)+θ2/π
最终该点等差线级数取两次测量的平均值
等倾线
1.等倾线的绘制
以正交平面偏振光场为例

P 为起偏镜偏振轴
A 为检偏镜偏振轴
P 垂直,A 水平时为 0 ∘ 0^\circ 0∘
为了保持正交平面偏振光场,所以要求 P 和 A 始终相互垂直
然后为了得到角度 θ \theta θ 的等倾线,将 P 和 A 同步旋转角度 θ \theta θ
2.等倾线图
将各个不同角度的等倾线画在一张图上,这张图成为等倾线图
由前面的分析可知,正交平面偏振光场中同时存在等差线和等倾线
为了避免等差线和等倾线互相干扰,可以使用光学敏感性较低的材料——有机玻璃
其材料条纹值 f 很大,根据 σ 1 − σ 2 = f N h \sigma_1 - \sigma_2 = f \frac {N} {h} σ1−σ2=fhN 可知,要出现条纹需要施加很大的载荷


图 圆盘对径受压的等倾线

图 圆盘对径受压的等倾线图
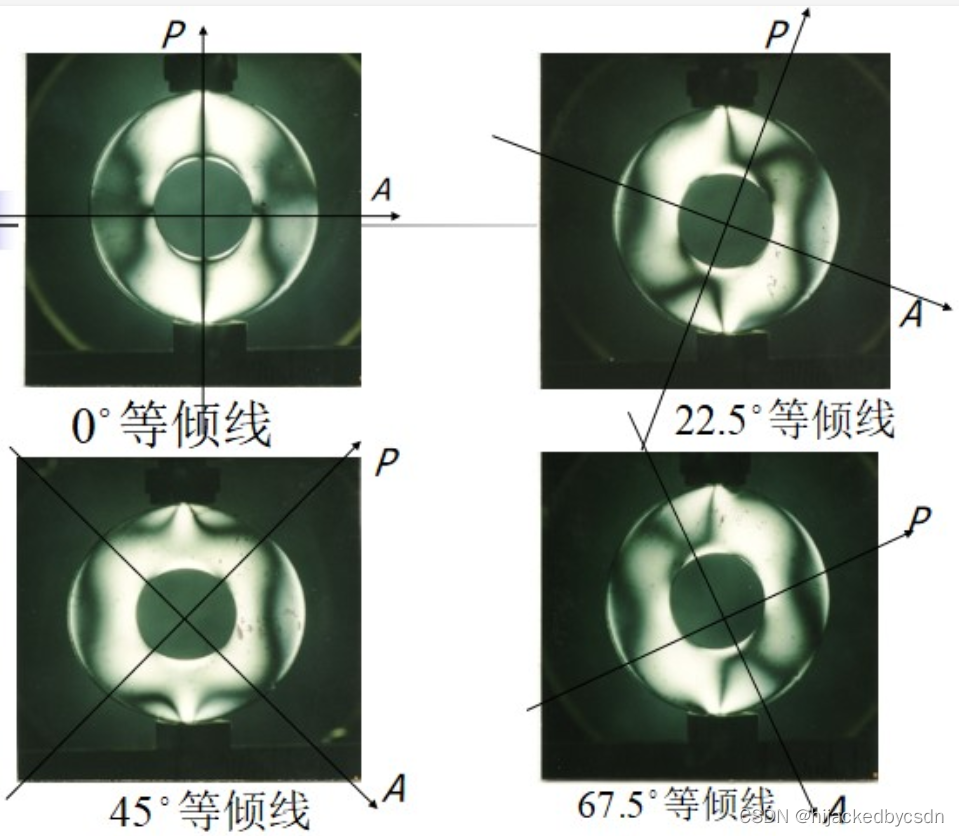
图 圆环对径受压的等倾线

图 圆环对径受压的等倾线图
等倾线的特征
1.自由曲线边界上

不受外载的模型边界称为自由边界
对于自由边界上的点,曲线的切线和法线方向就是此点的主应力方向
若某一等倾线与边界相交,且交点处模型边界的切线或法线与水平轴成 θ \theta θ 角,那么由等倾线上各点主应力方向相同的定义,有:
该等倾线上的各点的主应力方向均与水平轴成 θ \theta θ 或 π / 2 + θ \pi/2 + \theta π/2+θ 角
2.直线边界上

因为边界上无剪应力,所以边界线即为应力主线
所以边界线与等倾线重合
3.对称轴上

当模型的几何形状和载荷都以某轴线为对称时,则对称轴必为应力主轴,它就是一条等倾线
4.各向同性点上
在各向同性点上, σ 1 − σ 2 = 0 \sigma_1 - \sigma_2 = 0 σ1−σ2=0,可得 σ 1 = σ 2 \sigma_1 = \sigma_2 σ1=σ2
这意味着应力圆与 x 轴的两个交点重合,即应力圆是一个点
所以各向同性点上的任意方向都是主应力方向(感觉这才是各向同性点的名称来源吧)
所以不同角度的等倾线都必须通过各向同性点
5.集中载荷作用点
-
从主应力方向的观点看,是一个各向同性点
-
从主应力大小的观点看,是一个发源点
主应力方向 σ 1 , σ 2 \sigma_1, \sigma_2 σ1,σ2 的判别
等倾线图可以通过“同一线上主应力方向相同”的定义,先确定线上一点的主应力方向,再确定线上其他点的主应力方向
但是两个方向中哪个是 σ 1 \sigma_1 σ1 哪个是 σ 2 \sigma_2 σ2 无法判别
(或者说怎么判别哪个主应力是拉哪个是压)
(以拉应力为正)
1.分析法

-
从等倾线图中选择若干条等倾线
-
力学分析:
中心点的应力状态为:在 x 方向为拉应力,在 y 方向为压应力
-
再根据应力变化的连续性,在等倾线上参考已知应力状态点,就可以确定两个主应力的正负
2.钉压法

左图中单元体单向受拉,钉压后条纹级数增加 右图中单元体单向受压,钉压后条纹级数减小
-
假设单元体单向受拉:
原: σ 1 > 0 , σ 2 = 0 \sigma_1 > 0, \sigma_2 = 0 σ1>0,σ2=0
钉压: σ 1 > 0 , σ 2 < 0 \sigma_1 > 0, \sigma_2 < 0 σ1>0,σ2<0
同时 σ 1 \sigma_1 σ1 保持不变,则有 σ 1 − σ 2 \sigma_1 - \sigma_2 σ1−σ2 增大,条纹级数增加
-
假设单元体单向受压:
原: σ 1 < 0 , σ 2 = 0 \sigma_1 < 0, \sigma_2 = 0 σ1<0,σ2=0
钉压: σ 1 < 0 , σ 2 < 0 \sigma_1 < 0, \sigma_2 < 0 σ1<0,σ2<0
同时 σ 1 \sigma_1 σ1 保持不变,则有 σ 1 − σ 2 \sigma_1 - \sigma_2 σ1−σ2 减小,条纹级数减小
平面光弹性应力计算
1.边界应力
2.应力集中
3.内部应力分离方法
1.求主应力和法
2.斜射法
3.剪应力差法
4.材料条纹值的测定
三维光弹性的冻结切片法
1.三维光弹性的冻结切片法
-
应力冻结
-
切片
-
平面应力分析
2.次主应力
三维光弹性效应
1.平面应力-光学定理
2.模型切片的正射法
-
切片在 XY 平面,光线沿 Z 方向垂直入射
-
切片在 XZ 平面,光线沿 Y 方向垂直入射
-
切片在 YZ 平面,光线沿 X 方向垂直入射
























 666
666

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








