前言
由于摄像机标定中会使用到旋转矩阵以及旋转向量的知识,所以就整理了一下有关与这一部分基础知识的笔记,并进行详细的数学推导。
旋转矩阵
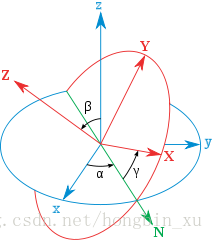
假设坐标系分别绕着 x x x轴旋转 ϕ \phi ϕ角,绕 y y y轴旋转 θ \theta θ角,绕 z z z轴旋转 ψ \psi ψ角,这里旋转的角度就是我们常说的pitch, roll, yaw。设任意某点在旋转前的坐标系中的坐标是 ( x , y , z ) (x,y,z) (x,y,z),旋转后的坐标是 ( x ′ , y ′ , z ′ ) (x^{'}, y^{'}, z^{'}) (x′,y′,z′)。
我们可以很容易地推导出这三种情况下的旋转矩阵:
- 绕X轴旋转φ角(PITCH):
R x = [ 1 0 0 0 cos ϕ − sin ϕ 0 sin ϕ cos ϕ ] R_x=\begin{bmatrix}1 & 0 & 0 \\ 0 & \cos{\phi} & -\sin{\phi} \\ 0 & \sin{\phi} & \cos{\phi} \end{bmatrix} Rx=⎣⎡1000cosϕsinϕ0−sinϕcosϕ⎦⎤
- 绕Y轴旋转θ角(ROLL):
R y = [ cos θ 0 sin θ 0 1 0 − sin θ 0 cos θ ] R_y=\begin{bmatrix} \cos{\theta} & 0 & \sin{\theta} \\ 0 & 1 & 0 \\ - \sin{\theta} & 0 & \cos{\theta} \end{bmatrix} Ry=⎣⎡cosθ0−sinθ010sinθ0cosθ⎦⎤
- 绕Z轴旋转ψ角(YAW):
R z = [ cos ψ − sin ψ 0 sin ψ cos ψ 0 0 0 1 ] R_z=\begin{bmatrix} \cos{\psi} & -\sin{\psi} & 0 \\ \sin{\psi} & \cos{\psi} & 0 \\ 0 & 0 & 1 \end{bmatrix} Rz=⎣⎡cosψsinψ0−sinψcosψ0001⎦⎤
详细步骤我就不列出来了,我以前的博客中有详细的推导步骤,虽然使用场景不同,但是概念都是一样的。(四旋翼姿态解算——基础理论及推导)
如果已经上面的三个角度 ϕ \phi ϕ、 θ \theta θ、 ψ \psi ψ,,我们可以通过将每一步的旋转矩阵相乘得到整个旋转矩阵。
R = R x ∗ R y ∗ R z R=R_x * R_y *R_z R=Rx∗Ry∗Rz
旋转向量
相机标定中表示旋转的方式,除了使用前面介绍的旋转矩阵之外,还可以使用旋转向量来表示。
我在网上搜索相关资料时,发现大多数都是直接给出了Rodrigue旋转向量的公式,而没有推导过程。如果只是拿来用,那肯定是没问题的,但是不把它的公式推导一遍,心里总是有点不踏实。(好吧,我知道我有点废话)下面我会给出我自己的证明步骤,在最后会给出公式。
补充概念:向量的拉格朗日公式
对于任意向量 a ⃗ ( a 1 , a 2 , a 3 ) \vec{a}(a_1,a_2,a_3) a(a1,a2,a3), b ⃗ ( b 1 , b 2 , b 3 ) \vec{b}(b_1,b_2,b_3) b(b1,b2,b3), c ⃗ ( c 1 , c 2 , c 3 ) \vec{c}(c_1,c_2,c_3) c(c1,c2,c3),有如下公式成立:
a ⃗ × ( b ⃗ × c ⃗ ) = ( a ⃗ ⋅ c ⃗ ) b ⃗ − ( a ⃗ ⋅ b ⃗ ) c ⃗ \vec{a} \times (\vec{b} \times \vec{c}) = (\vec{a} \cdot \vec{c})\vec{b} - (\vec{a} \cdot \vec{b}) \vec{c} a×(b×c)=(a⋅c)b−(a⋅b)c
证明如下:
设 d ⃗ = b ⃗ × c ⃗ \vec{d} = \vec{b} \times \vec{c} d=b×c,且可表示为 d ⃗ ( d 1 , d 2 , d 3 ) \vec{d}(d_1,d_2,d_3) d(d1,d2,d3)。
则有: d ⃗ = b ⃗ × c ⃗ = [ i ⃗ j ⃗ k ⃗ b 1 b 2 b 3 c 1 c 2 c 3 ] = i ⃗ ( b 2 c 3 − b 3 c 2 ) − j ⃗ ( b 1 c 3 − b 3 c 1 ) + k ⃗ ( b 1 c 2 − b 2 c 1 ) \vec{d} = \vec{b} \times \vec{c}=\begin{bmatrix} \vec{i} & \vec{j} & \vec{k} \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3 \end{bmatrix}\\=\vec{i}(b_2c_3-b_3c_2)-\vec{j}(b_1c_3-b_3c_1)+\vec{k}(b_1c_2-b_2c_1) d=b×c=⎣⎡ib1c1jb2c2kb3c3⎦⎤=i(b2c3−b3c2)−j(b1c3−b3c1)+k(b1c2−b2c1)
对应地就有: d 1 = b 2 c 3 − b 3 c 2 d_1=b_2c_3-b_3c_2 d1=b2c3−b3c2、 d 2 = b 3 c 1 − b 1 c 3 d_2=b_3c_1-b_1c_3 d2=b3c1−b1c3、 d 3 = b 1 c 2 − b 2 c 1 d_3=b_1c_2-b_2c_1 d3=b1c2−b2c1。
再设 e ⃗ = a ⃗ × d ⃗ = a ⃗ × ( b ⃗ × c ⃗ ) \vec{e} = \vec{a} \times \vec{d} = \vec{a} \times (\vec{b} \times \vec{c}) e=a×d=a×(b×c),且可表示为 e ⃗ ( e 1 , e 2 , e 3 ) \vec{e}(e_1,e_2,e_3) e(e1,e2,e3)。
那么: e ⃗ = a ⃗ × d ⃗ = [ i ⃗ j ⃗ k ⃗ a 1 a 2 a 3 d 1 d 2 d 3 ] = i ⃗ ( a 2 d 3 − a 3 d 2 ) − j ⃗ ( a 1 d 3 − a 3 d 1 ) + k ⃗ ( a 1 d 2 − a 2 d 1 ) \vec{e} = \vec{a} \times \vec{d}=\begin{bmatrix} \vec{i} & \vec{j} & \vec{k} \\ a_1 & a_2 & a_3 \\ d_1 & d_2 & d_3 \end{bmatrix}\\=\vec{i}(a_2d_3-a_3d_2)-\vec{j}(a_1d_3-a_3d_1)+\vec{k}(a_1d_2-a_2d_1) e=a×d=⎣⎡ia1d1ja2d2ka3d3⎦⎤=i(a2d3−a3d2)−j(a1d3−a3d1)+k(a1d2−a2d1)
对应地得到得到: e 1 = a 2 d 3 − a 3 d 2 e_1=a_2d_3-a_3d_2 e1=a2d3−a3d2、 e 2 = a 1 d 3 − a 3 d 1 e_2=a_1d_3-a_3d_1 e2=a1d3−a3d1、 e 3 = a 1 d 2 − a 2 d 1 e_3=a_1d_2-a_2d_1 e3=a1d2−a2d1
对于 e 1 e_1 e1,代入前面推导出来的 d 2 d_2 d2、 d 3 d_3 d3:
e 1 = a 2 d 3 − a 3 d 2 = a 2 ( b 1 c 2 − b 2 c 1 ) − a 3 ( b 3 c 1 − b 1 c 3 ) = b 1 ( a 2 c 2 + a 3 c 3 ) − c 1 ( a 3 b 3 + a 2 b 2 ) = b 1 ( a ⃗ ⋅ c ⃗ − a 1 c 1 ) − c 1 ( a ⃗ ⋅ b ⃗ − a 1 b 1 ) = b 1 ( a ⃗ ⋅ c ⃗ ) − c 1 ( a ⃗ ⋅ b ⃗ ) e_1=a_2d_3-a_3d_2=a_2(b_1c_2-b_2c_1)-a_3(b_3c_1-b_1c_3) \\ =b_1 (a_2c_2 + a_3c_3) - c_1 (a_3b_3 + a_2b_2) \\ = b_1 (\vec{a} \cdot \vec{c} - a_1c_1) - c_1 (\vec{a} \cdot \vec{b} - a_1b_1) \\ = b_1 (\vec{a} \cdot \vec{c}) - c_1 (\vec{a} \cdot \vec{b}) e1=a2d3−a3d2=a2(b1c2−b2c1)−a3(b3c1−b1c3)=b1(a2c2+a3c3)−c1(a3b3+a2b2)=b1(a⋅c−a1c1)−c1(a⋅b−a1b1)=b1(a⋅c)−c1(a⋅b)
同理可得:
e 2 = b 2 ( a ⃗ ⋅ c ⃗ ) − c 2 ( a ⃗ ⋅ b ⃗ ) e_2 = b_2 (\vec{a} \cdot \vec{c}) - c_2 (\vec{a} \cdot \vec{b}) e2=b2(a⋅c)−c2(a⋅b)
e 3 = b 3 ( a ⃗ ⋅ c ⃗ ) − c 3 ( a ⃗ ⋅ b ⃗ ) e_3 = b_3 (\vec{a} \cdot \vec{c}) - c_3 (\vec{a} \cdot \vec{b}) e3=b3(a⋅c)−c3(a⋅b)
把这三个式子合并,表示成向量形式:
e ⃗ = b ⃗ ( a ⃗ ⋅ c ⃗ ) − c ⃗ ( a ⃗ ⋅ b ⃗ ) \vec{e} = \vec{b} (\vec{a} \cdot \vec{c}) - \vec{c} (\vec{a} \cdot \vec{b}) e=b(a⋅c)−c(a⋅b)
证明完毕,后面我们还会用到这个公式。
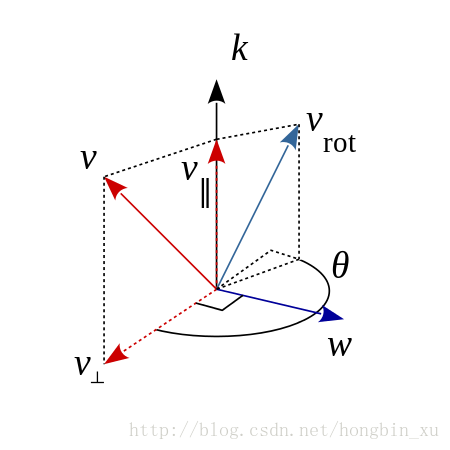
上图摘自维基百科。假设我们在任意空间中有任意一个向量 v ⃗ \vec{v} v, k ⃗ \vec{k} k是某个单位向量。现在,我们将向量 v ⃗ \vec{v} v以单位向量 k ⃗ \vec{k} k为轴,旋转任意角度 θ \theta θ,得到旋转后的向量 v r o t ⃗ \vec{v_{rot}} vrot如图中所示。在图中,我们将 v ⃗ \vec{v} v关于 k ⃗ \vec{k} k做正交分解(高中物理),会得到两个新的向量: v ⊥ ⃗ \vec{v_{\bot}} v⊥和 v ∥ ⃗ \vec{v_{\parallel}} v∥。
很明显: v ⊥ ⃗ \vec{v_{\bot}} v⊥与 k ⃗ \vec{k} k相互垂直, v ∥ ⃗ \vec{v_{\parallel}} v∥与 k ⃗ \vec{k} k共线(平行),且还有 v ⃗ = v ⊥ ⃗ + v ∥ ⃗ \vec{v}=\vec{v_{\bot}}+\vec{v_{\parallel}} v=v⊥+v∥。
因为 v ∥ ⃗ \vec{v_{\parallel}} v∥与 k ⃗ \vec{k} k共线,且 k ⃗ \vec{k} k是一个单位向量,所以:
v ∥ ⃗ = ∥ v ∥ ⃗ ∥ ⋅ k ⃗ = v ⃗ ⋅ k ⃗ ∥ k ⃗ ∥ ⋅ k ⃗ = ( v ⃗ ⋅ k ⃗ ) ⋅ k ⃗ \vec{v_{\parallel}}=\|\vec{v_{\parallel}}\| \cdot \vec{k}= \frac{\vec{v} \cdot \vec{k}}{\| \vec{k} \|} \cdot \vec{k} = (\vec{v} \cdot \vec{k}) \cdot \vec{k} v∥=∥v∥∥⋅k=∥k∥v⋅k⋅k=(v⋅k)⋅k
接下来求 v ⊥ ⃗ \vec{v_{\bot}} v⊥,由我们前面推导的向量的拉格朗日定理: a ⃗ × ( b ⃗ × c ⃗ ) = ( a ⃗ ⋅ c ⃗ ) b ⃗ − ( a ⃗ ⋅ b ⃗ ) c ⃗ \vec{a} \times (\vec{b} \times \vec{c}) = (\vec{a} \cdot \vec{c})\vec{b} - (\vec{a} \cdot \vec{b}) \vec{c} a×(b×c)=(a⋅c)b−(a⋅b)c,有:
k ⃗ × ( k ⃗ × v ⃗ ) = ( k ⃗ ⋅ v ⃗ ) ⋅ k ⃗ − ( k ⃗ ⋅ k ⃗ ) ⋅ v ⃗ = ( k ⃗ ⋅ v ⃗ ) ⋅ k ⃗ − v ⃗ \vec{k} \times (\vec{k} \times \vec{v}) = (\vec{k} \cdot \vec{v}) \cdot \vec{k} - (\vec{k} \cdot \vec{k}) \cdot \vec{v}=(\vec{k} \cdot \vec{v}) \cdot \vec{k} - \vec{v} k×(k×v)=(k⋅v)⋅k−(k⋅k)⋅v=(k⋅v)⋅k−v
然后,我们就可以推出:
v ⊥ ⃗ = v ⃗ − v ∥ ⃗ = − k ⃗ × ( k ⃗ × v ⃗ ) \vec{v_{\bot}}=\vec{v} - \vec{v_{\parallel}} = -\vec{k} \times (\vec{k} \times \vec{v}) v⊥=v−v∥=−k×(k×v)
我们可以根据前面给出的示意图来直观地理解这些式子: k ⃗ × v ⃗ \vec{k} \times \vec{v} k×v可以看作是 v ⊥ ⃗ \vec{v_{\bot}} v⊥绕着 k ⃗ \vec{k} k逆时针旋转90度得到的,即图中的 w ⃗ = k ⃗ × v ⃗ \vec{w}=\vec{k} \times \vec{v} w=k×v;对于 k ⃗ × ( k ⃗ × v ⃗ ) = k ⃗ × w ⃗ \vec{k} \times (\vec{k} \times \vec{v})=\vec{k} \times\vec{w} k×(k×v)=k×w,在图中观察发现,这个式子的结果其实就是 v ⊥ ⃗ \vec{v_{\bot}} v⊥绕着 k ⃗ \vec{k} k逆时针旋转180度得到的结果,共线且夹角为180度,正好对应推导出的结果: v ⊥ ⃗ = − k ⃗ × ( k ⃗ × v ⃗ ) \vec{v_{\bot}} = -\vec{k} \times (\vec{k} \times \vec{v}) v⊥=−k×(k×v)。
还是根据这幅图来看,旋转过程中 v ∥ ⃗ \vec{v_{\parallel}} v∥的大小始终不变,因为它是 v ⃗ \vec{v} v在 k ⃗ \vec{k} k方向上的投影,就在旋转轴上,自然不会变。所以有: v r o t , ∥ ⃗ = v ∥ ⃗ \vec{v_{rot, \parallel}} = \vec{v_{\parallel}} vrot,∥=v∥。
接下来看 v r o t , ⊥ ⃗ \vec{v_{rot, \bot}} vrot,⊥的变化:
首先,可以肯定的是旋转过程中矢量的模长不变,只会改变方向,所以: ∥ v r o t , ⊥ ⃗ ∥ = ∥ v ⊥ ⃗ ∥ \| \vec{v_{rot, \bot}} \| = \| \vec{v_{\bot}} \| ∥vrot,⊥∥=∥v⊥∥。
我们可以由 v ⊥ ⃗ \vec{v_{\bot}} v⊥和 k ⃗ \vec{k} k方向的投影,组合得到 v r o t , ⊥ ⃗ \vec{v_{rot, \bot}} vrot,⊥:
v r o t , ⊥ ⃗ = v ⊥ ⃗ cos θ + ∥ v ⊥ ⃗ ∥ sin θ w ⃗ ∥ w ⃗ ∥ \vec{v_{rot, \bot}}=\vec{v_{\bot}}\cos\theta + \| \vec{v_{\bot}} \| \sin\theta \frac{\vec{w}}{\|\vec{w}\|} vrot,⊥=v⊥cosθ+∥v⊥∥sinθ∥w∥w
前面有: w ⃗ = k ⃗ × v ⃗ \vec{w}=\vec{k} \times \vec{v} w=k×v可以看作是 v ⊥ ⃗ \vec{v_{\bot}} v⊥绕着 k ⃗ \vec{k} k逆时针旋转90度得到的。那么有: ∥ v ⊥ ⃗ ∥ = ∥ w ⃗ ∥ \| \vec{v_{\bot}} \| = \|\vec{w}\| ∥v⊥∥=∥w∥。
上式可以化简为:
v r o t , ⊥ ⃗ = v ⊥ ⃗ cos θ + sin θ w ⃗ = v ⊥ ⃗ cos θ + sin θ ( k ⃗ × v ⃗ ) \vec{v_{rot, \bot}} = \vec{v_{\bot}}\cos\theta + \sin\theta \vec{w}= \vec{v_{\bot}}\cos\theta + \sin\theta (\vec{k} \times \vec{v}) vrot,⊥=v⊥cosθ+sinθw=v⊥cosθ+sinθ(k×v)
将 v r o t , ⊥ ⃗ \vec{v_{rot, \bot}} vrot,⊥和 v r o t , ∥ ⃗ \vec{v_{rot, \parallel}} vrot,∥相加,即可得到 v r o t ⃗ \vec{v_{rot}} vrot:
v r o t ⃗ = v r o t , ⊥ ⃗ + v r o t , ∥ ⃗ = v ∥ ⃗ + v ⊥ ⃗ cos θ + sin θ ( k ⃗ × v ⃗ ) = v ∥ ⃗ + ( v ⃗ − v ∥ ⃗ ) cos θ + sin θ ( k ⃗ × v ⃗ ) = v ⃗ cos θ + ( 1 − cos θ ) v ∥ ⃗ + sin θ ( k ⃗ × v ⃗ ) \begin{aligned} \vec{v_{rot}} &= \vec{v_{rot, \bot}} + \vec{v_{rot, \parallel}} \\ &= \vec{v_{\parallel}} + \vec{v_{\bot}}\cos\theta + \sin\theta (\vec{k} \times \vec{v}) \\ &= \vec{v_{\parallel}} + (\vec{v} - \vec{v_{\parallel}}) \cos\theta +\sin\theta (\vec{k} \times \vec{v}) \\ &= \vec{v}\cos\theta + (1-\cos\theta) \vec{v_{\parallel}} + \sin\theta (\vec{k} \times \vec{v}) \end{aligned} vrot=vrot,⊥+vrot,∥=v∥+v⊥cosθ+sinθ(k×v)=v∥+(v−v∥)cosθ+sinθ(k×v)=vcosθ+(1−cosθ)v∥+sinθ(k×v)
前面推出来了: v ∥ ⃗ = ∥ v ∥ ⃗ ∥ ⋅ k ⃗ = v ⃗ ⋅ k ⃗ ∥ k ⃗ ∥ ⋅ k ⃗ = ( v ⃗ ⋅ k ⃗ ) ⋅ k ⃗ \vec{v_{\parallel}}=\|\vec{v_{\parallel}}\| \cdot \vec{k}= \frac{\vec{v} \cdot \vec{k}}{\| \vec{k} \|} \cdot \vec{k} = (\vec{v} \cdot \vec{k}) \cdot \vec{k} v∥=∥v∥∥⋅k=∥k∥v⋅k⋅k=(v⋅k)⋅k,直接把那个结论代入这里。
v r o t ⃗ = v ⃗ cos θ + ( 1 − cos θ ) ( v ⃗ ⋅ k ⃗ ) ⋅ k ⃗ + sin θ ( k ⃗ × v ⃗ ) \begin{aligned} \vec{v_{rot}} &= \vec{v}\cos\theta + (1-\cos\theta) (\vec{v} \cdot \vec{k}) \cdot \vec{k} + \sin\theta (\vec{k} \times \vec{v}) \end{aligned} vrot=vcosθ+(1−cosθ)(v⋅k)⋅k+sinθ(k×v)
现在我们已经推导出了旋转向量公示了,我们可以套用这个公式来表示任意旋转。
接下来要进一步整理成矩阵形式:
对于 k ⃗ × v ⃗ \vec{k} \times \vec{v} k×v,用矩阵形式来表示:(无非就是向量叉乘,拆成三个轴上的分量来表示)
[ ( k ⃗ × v ⃗ ) x ( k ⃗ × v ⃗ ) y ( k ⃗ × v ⃗ ) z ] = [ k y v z − k z v y k z v x − k x v z k x v y − k y v x ] = [ 0 − k z k y k z 0 − k x − k y k x 0 ] ⋅ [ v x v y v z ] \begin{bmatrix} (\vec{k} \times \vec{v})_x \\ (\vec{k} \times \vec{v})_y \\ (\vec{k} \times \vec{v})_z \end{bmatrix} = \begin{bmatrix}k_yv_z-k_zv_y \\ k_zv_x-k_xv_z \\ k_xv_y - k_yv_x \end{bmatrix} = \begin{bmatrix} 0 & -k_z & k_y \\ k_z & 0 & -k_x \\ -k_y & k_x &0 \end{bmatrix} \cdot \begin{bmatrix} v_x \\ v_y \\ v_z\end{bmatrix} ⎣⎢⎡(k×v)x(k×v)y(k×v)z⎦⎥⎤=⎣⎡kyvz−kzvykzvx−kxvzkxvy−kyvx⎦⎤=⎣⎡0kz−ky−kz0kxky−kx0⎦⎤⋅⎣⎡vxvyvz⎦⎤
使用一个大写的 K K K来表示:
K = [ 0 − k z k y k z 0 − k x − k y k x 0 ] K=\begin{bmatrix} 0 & -k_z & k_y \\ k_z & 0 & -k_x \\ -k_y & k_x &0 \end{bmatrix} K=⎣⎡0kz−ky−kz0kxky−kx0⎦⎤
那么有: K v ⃗ = k ⃗ × v ⃗ K\vec{v}=\vec{k} \times \vec{v} Kv=k×v
还有: K ( K v ⃗ ) = K 2 v ⃗ = K ( k ⃗ × v ⃗ ) = k ⃗ × ( K v ⃗ ) = k ⃗ × ( k ⃗ × v ⃗ ) K(K\vec{v})=K^2\vec{v}=K(\vec{k} \times \vec{v}) = \vec{k} \times (K\vec{v}) = \vec{k} \times (\vec{k} \times \vec{v}) K(Kv)=K2v=K(k×v)=k×(Kv)=k×(k×v)
公式可以进一步化简为:
v r o t ⃗ = v ⃗ cos θ + ( 1 − cos θ ) ( v ⃗ ⋅ k ⃗ ) ⋅ k ⃗ + sin θ ( k ⃗ × v ⃗ ) = v ⃗ cos θ + ( 1 − cos θ ) ( v ⃗ + k ⃗ × ( k ⃗ × v ⃗ ) ) + sin θ ( k ⃗ × v ⃗ ) = v ⃗ + ( 1 − cos θ ) K 2 v ⃗ + s i n θ K v ⃗ \begin{aligned} \vec{v_{rot}} &= \vec{v}\cos\theta + (1-\cos\theta) (\vec{v} \cdot \vec{k}) \cdot \vec{k} + \sin\theta (\vec{k} \times \vec{v}) \\ &= \vec{v}\cos\theta + (1-\cos\theta) (\vec{v} + \vec{k} \times (\vec{k} \times \vec{v})) + \sin\theta (\vec{k} \times \vec{v}) \\ &= \vec{v} + (1-\cos\theta)K^2\vec{v} + sin\theta K \vec{v} \end{aligned} vrot=vcosθ+(1−cosθ)(v⋅k)⋅k+sinθ(k×v)=vcosθ+(1−cosθ)(v+k×(k×v))+sinθ(k×v)=v+(1−cosθ)K2v+sinθKv
给出旋转矩阵 R R R有: v r o t ⃗ = R v ⃗ \vec{v_{rot}} = R \vec{v} vrot=Rv
那么消去 v ⃗ \vec{v} v:$R = I + (1-\cos\theta)K^2 + sin\theta K $
Rodrigue旋转向量公式
已知单位向量 k ⃗ = ( k x , k y , k z ) \vec{k}=(k_x,k_y,k_z) k=(kx,ky,kz),向量 v ⃗ \vec{v} v绕着它旋转 θ \theta θ角。旋转后的向量 v r o t ⃗ \vec{v_{rot}} vrot可以通过如下公式求得:
v r o t ⃗ = v ⃗ cos θ + ( 1 − cos θ ) ( v ⃗ ⋅ k ⃗ ) ⋅ k ⃗ + sin θ ( k ⃗ × v ⃗ ) \begin{aligned} \vec{v_{rot}} &= \vec{v}\cos\theta + (1-\cos\theta) (\vec{v} \cdot \vec{k}) \cdot \vec{k} + \sin\theta (\vec{k} \times \vec{v}) \end{aligned} vrot=vcosθ+(1−cosθ)(v⋅k)⋅k+sinθ(k×v)
我们可以把 v ⃗ \vec{v} v提取出来,就得到了:
v r o t ⃗ = R v ⃗ = ( I ⋅ cos θ + ( 1 − cos θ ) k ⃗ ⋅ k ⃗ + sin θ K ) v ⃗ \begin{aligned} \vec{v_{rot}} &= R \vec{v} \\ &= (I \cdot \cos\theta + (1-\cos\theta) \vec{k} \cdot \vec{k} + \sin\theta K)\vec{v} \end{aligned} vrot=Rv=(I⋅cosθ+(1−cosθ)k⋅k+sinθK)v
其中:
K = [ 0 − k z k y k z 0 − k x − k y k x 0 ] K=\begin{bmatrix} 0 & -k_z & k_y \\ k_z & 0 & -k_x \\ -k_y & k_x &0 \end{bmatrix} K=⎣⎡0kz−ky−kz0kxky−kx0⎦⎤
根据上面这个式子,我们可以给出Rodrigue旋转公式:
对于旋转向量
r
⃗
=
(
r
x
,
r
y
,
r
z
)
\vec{r} = (r_x, r_y, r_z)
r=(rx,ry,rz):
θ \theta θ为向量 r ⃗ \vec{r} r的模长,而且要保证向量 r ⃗ \vec{r} r是一个单位向量。
反变换也可以很容易求出:
注:在opencv中有相关的实现(Rodrigues2函数)
当然还有一种写法:
v r o t ⃗ = R v ⃗ = I ⋅ v ⃗ + ( 1 − cos θ ) K 2 ⋅ v ⃗ + s i n θ K ⋅ v ⃗ \vec{v_{rot}} = R\vec{v} = I \cdot \vec{v} + (1-\cos\theta)K^2 \cdot \vec{v} + sin\theta K \cdot \vec{v} vrot=Rv=I⋅v+(1−cosθ)K2⋅v+sinθK⋅v
对应的旋转矩阵:(我们可以用这个公式来求旋转矩阵)
R = I + ( 1 − cos θ ) K 2 + s i n θ K R = I + (1-\cos\theta)K^2 + sin\theta K R=I+(1−cosθ)K2+sinθK
其中:
K = [ 0 − k z k y k z 0 − k x − k y k x 0 ] K=\begin{bmatrix} 0 & -k_z & k_y \\ k_z & 0 & -k_x \\ -k_y & k_x &0 \end{bmatrix} K=⎣⎡0kz−ky−kz0kxky−kx0⎦⎤
参考链接:





 本文详细介绍了旋转矩阵的概念及其数学推导过程,并通过拉格朗日公式辅助理解。同时,文章深入探讨了旋转向量表示法,包括Rodrigues公式推导,最终给出了旋转矩阵的计算公式。
本文详细介绍了旋转矩阵的概念及其数学推导过程,并通过拉格朗日公式辅助理解。同时,文章深入探讨了旋转向量表示法,包括Rodrigues公式推导,最终给出了旋转矩阵的计算公式。
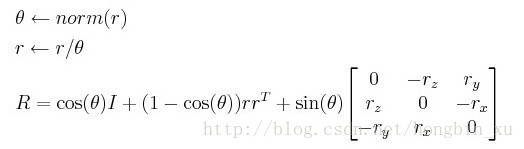
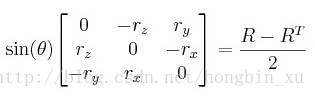
















 2894
2894










