本文探讨了三重积分在几何中的应用，通过类比土豆的不同切法，深入浅出地解释了投影法和截面法的概念。文章重点介绍了如何利用这两种方法计算空间区域的体积，并讨论了对称区域上积分的特性。
1. 问题的引入——三重积分的实际背景
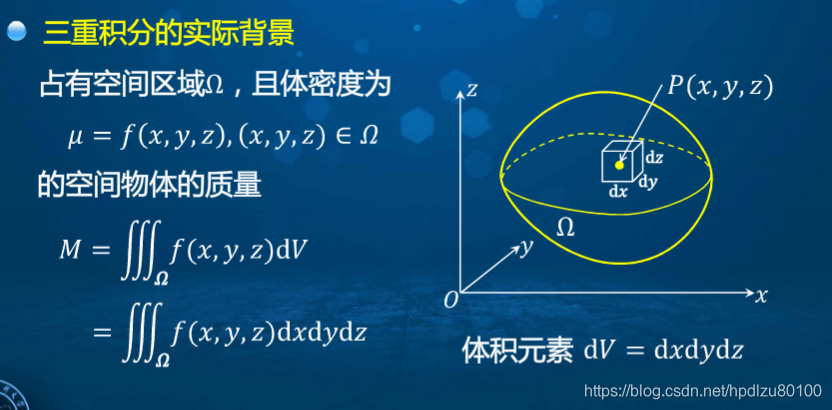
土豆的切法（切丝、切片、切丁）与三重积分的关系（先一后二法——投影法、先二后一法——截面法）
2. 投影法（投影区域积分法，先一后二法，切丝法）
1. 空间积分区域的类型（关于z轴的简单区域）
2. 三重积分计算的“先一后二”法——投影法
通常，用更简单的形式记为：
3. 截面法（先二后一法，切片法）
4. 对称区域上的三重积分（偶倍奇零）
扫一扫
653
评论
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
查看更多评论
添加红包
