10.3 三重积分

10.3 三重积分

一、三重积分的概念

定积分及二重积分作为和的极限的概念，可以很自然地推广到三重积分。定义设 f(x,y,z)f(x,y,z)f(x,y,z) 是空间有界闭区域 Ω\OmegaΩ 上的有界函数。将 Ω\OmegaΩ 任意分成 nnn 个小闭区域 ΔV1,ΔV2,…,ΔVn\Delta V_1, \Delta V_2, \ldots, \Delta V_nΔV1​,ΔV2​,…,ΔVn​，其中 ΔVi\Delta V_iΔVi​ 表示第 iii 个小闭区域，也表示它的体积。在每个 ΔVi\Delta V_iΔVi​ 上任取一点 (ξi,ηi,ζi)(\xi_i, \eta_i, \zeta_i)(ξi​,ηi​,ζi​)，作乘积

如果当各小闭区域直径中的最大值 λ→0\lambda \to 0λ→0 时，这和的极限总存在，且与闭区域 Ω\OmegaΩ 的分法及点 (ξi,ηi,ζi)(\xi_i, \eta_i, \zeta_i)(ξi​,ηi​,ζi​) 的取法无关，那么称此极限为函数 f(x,y,z)f(x, y, z)f(x,y,z) 在闭区域 Ω\OmegaΩ 上的三重积分，即积分。记作：

其中 f(x,y,z)f(x, y, z)f(x,y,z) 叫做被积函数，dVdVdV 叫做体积元素，Ω\OmegaΩ 叫做积分区域。

其中 dx dy dzdx \, dy \, dzdxdydz 叫做直角坐标系中的体积元素。

当函数 f(x,y,z)f(x, y, z)f(x,y,z) 在闭区域 Ω\OmegaΩ 上连续时，上式右端的和的极限必定存在，也就是函数 f(x,y,z)f(x, y, z)f(x,y,z) 在闭区域 Ω\OmegaΩ 上的三重积分必定存在。以后我们总假定函数 f(x,y,z)f(x, y, z)f(x,y,z) 在闭区域 Ω\OmegaΩ 上是连续的。三重积分的性质与第一节中所叙述的二重积分的性质类似，这里不再重复了。

如果 f(x,y,z)f(x, y, z)f(x,y,z) 表示某物体在点 (x,y,z)(x, y, z)(x,y,z) 处的密度，Ω\OmegaΩ 是该物体所占有的空间闭区域，且 f(x,y,z)f(x, y, z)f(x,y,z) 在 Ω\OmegaΩ 上连续，那么

是该物体的质量 mmm 的近似值，这个和当 λ→0\lambda \to 0λ→0 时的极限就是该物体的质量 mmm，所以：

二、三重积分的计算

计算三重积分的基本方法是将三重积分化为三次积分来计算。下面按利用不同的坐标来分别讨论将三重积分化为三次积分的方法，且只限于叙述方法。

1. 利用直角坐标计算三重积分

假设平行于 zzz 轴且穿过闭区域 Ω\OmegaΩ 内部的直线与闭区域 Ω\OmegaΩ 的边界曲面 SSS 相交不多于两点。把闭区域 Ω\OmegaΩ 投影到 xOyxOyxOy 面上，得一平面闭区域 D1D_1D1​（图 10-29）。以 D1D_1D1​ 的边界为准线作母线平行于 zzz 轴的柱面。这柱面与曲面 SSS 的交线从 SSS 中分出的上、下两部分，它们的方程分别为

其中 z1(x,y)z_1(x, y)z1​(x,y) 与 z2(x,y)z_2(x, y)z2​(x,y) 都是 D1D_1D1​ 上的连续函数，且 z1(x,y)≤z2(x,y)z_1(x, y) \leq z_2(x, y)z1​(x,y)≤z2​(x,y)。过 D1D_1D1​ 内任一点 (x,y)(x, y)(x,y) 作平行于 zzz 轴的直线，这直线通过曲面 S1S_1S1​ 穿入 Ω\OmegaΩ 内，然后通过曲面 S2S_2S2​ 穿出 Ω\OmegaΩ 外，穿入点与穿出点的竖坐标分别为 z1(x,y)z_1(x, y)z1​(x,y) 与 z2(x,y)z_2(x, y)z2​(x,y)。

在这种情形下，积分区域 Ω\OmegaΩ 可表示为

先将 xxx、yyy 看做定值，将 (x,y,z)(x, y, z)(x,y,z) 只看做 zzz 的函数，在区间 [z1(x,y),z2(x,y)][z_1(x, y), z_2(x, y)][z1​(x,y),z2​(x,y)] 上对 zzz 积分。积分的结果是 xxx、yyy 的函数，记为 F(x,y)F(x, y)F(x,y)，即

然后计算 F(x,y)F(x, y)F(x,y) 在闭区域 D1D_1D1​ 上的二重积分

假如闭区域

把这个二重积分化为二次积分，于是得到三重积分的计算公式

公式（3-2）把三重积分化为先对 zzz、次对 yyy、最后对 xxx 的三次积分。

如果平行于 xxx 轴或 yyy 轴且穿过闭区域 Ω\OmegaΩ 内部的直线与 Ω\OmegaΩ 的边界曲面 SSS 相交不多于两点，也可把闭区域 Ω\OmegaΩ 投影到 yOzyOzyOz 面上或 xOzxOzxOz 面上，这样便可把三重积分化为按其他顺序的三次积分。如果平行于坐标轴且穿过闭区域 Ω\OmegaΩ 内部的直线与边界曲面 SSS 的交点多于两个，也可像处理二重积分那样，把 Ω\OmegaΩ 分成若干部分，使 Ω\OmegaΩ 上的三重积分化为各部分闭区域上的三重积分的和。

例1 计算三重积分 ∭Ωf(x,y,z) dV\iiint_\Omega f(x, y, z) \, dV∭Ω​f(x,y,z)dV，其中 Ω\OmegaΩ 为三个坐标面及平面 x+2y+z=1x + 2y + z = 1x+2y+z=1 所围成的闭区域。

解：作闭区域 Ω\OmegaΩ 如图 10-30 所示。将 Ω\OmegaΩ 投影到 xOyxOyxOy 面上，得投影区域 D1D_1D1​ 为三角形闭区域 OABOABOAB。直线 OAOAOA、OBOBOB 及 ABABAB 的方程依次为 y=0y = 0y=0、x=0x = 0x=0 及 x+2y=1x + 2y = 1x+2y=1，所以

在 D1D_1D1​ 内任取一点 (x,y)(x, y)(x,y)，过此点作平行于 zzz 轴的直线，该直线通过平面 z=0z = 0z=0 穿入 Ω\OmegaΩ 内，然后通过平面 z=1−x−2yz = 1 - x - 2yz=1−x−2y 穿出 Ω\OmegaΩ 外。

于是，由公式（3-2）得

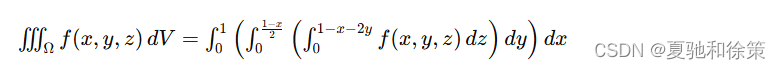
有时，我们计算一个三重积分也可以化为先计算一个二重积分，再计算一个定积分，即有下述计算公式。

设空间闭区域

其中 DzD_zDz​ 是竖坐标为 zzz 的平面截闭区域 Ω\OmegaΩ 所得到的一个平面闭区域（图 10-31），则有

解：空间闭区域 Ω\OmegaΩ 可表示为

如图 10-32 所示。由公式（3-3）得

2. 利用柱面坐标计算三重积分

设 M(x,y,z)M(x, y, z)M(x,y,z) 为空间内一点，并设点 MMM 在 xOyxOyxOy 面上的投影 PPP 的极坐标为 (p,θ)(p, \theta)(p,θ)，则这样的三个数 (p,θ,z)(p, \theta, z)(p,θ,z) 就叫做点 MMM 的柱面坐标（图 10-33），这里规定 ppp、θ\thetaθ、zzz 的变化范围为

显然，点 MMM 的直角坐标与柱面坐标的关系为

现在要把三重积分 ∭Ωf(x,y,z) dV\iiint_\Omega f(x, y, z) \, dV∭Ω​f(x,y,z)dV 变换为柱面坐标。为此，用三组坐标面 p=常数p = \text{常数}p=常数、θ=常数\theta = \text{常数}θ=常数、z=常数z = \text{常数}z=常数 把 Ω\OmegaΩ 分成许多小闭区域，除了含 Ω\OmegaΩ 的边界点的一些不规则小闭区域外，这种小闭区域都是柱体。今考虑由 ppp、θ\thetaθ 和 zzz 各取得微小增量 dpdpdp、dθd\thetadθ 和 dzdzdz 所成的柱体的体积（图 10-34）。这个体积等于高与底面积的乘积。现在高为 dzdzdz、底面积在不计高阶无穷小时为 p dp dθp \, dp \, d\thetapdpdθ（即极坐标系中的面积元素），于是得

这就是柱面坐标系中的体积元素。再注意到关系式（3-4），就有

其中 F(p,θ,z)=f(pcos⁡θ,psin⁡θ,z)F(p, \theta, z) = f(p \cos \theta, p \sin \theta, z)F(p,θ,z)=f(pcosθ,psinθ,z)。这就是把三重积分的变量从直角坐标变换为柱面坐标的公式。至于变量变换为柱面坐标后的三重积分的计算，则可化为三次积分来进行。化为三次积分时，积分限是根据 ppp、θ\thetaθ 和 zzz 在积分区域 Ω\OmegaΩ 中的变化范围来确定的，下面通过例子来说明。

解：把闭区域 Ω\OmegaΩ 投影到 xOyxOyxOy 面上，得半径为 2 的圆形闭区域

在 DDD 内任取一点 (p,θ)(p, \theta)(p,θ)，过此点作平行于 zzz 轴的直线，此直线通过曲面 z=p2z = p^2z=p2 穿入 Ω\OmegaΩ 内，然后通过平面 z=4z = 4z=4 穿出 Ω\OmegaΩ 外。因此闭区域 Ω\OmegaΩ 可用不等式

来表示。于是

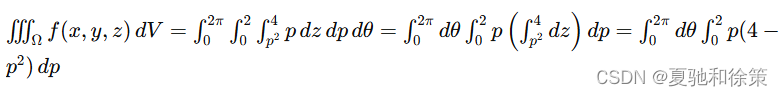
计算得

3. 利用球面坐标计算三重积分

设 M(x,y,z)M(x, y, z)M(x,y,z) 为空间内一点，则点 MMM 也可用这样三个有次序的数 rrr、ϕ\phiϕ 和 θ\thetaθ 来确定，其中 rrr 为原点 OOO 与点 MMM 间的距离，ϕ\phiϕ 为有向线段 OMOMOM 与 zzz 轴正向所夹的角，θ\thetaθ 为从正 zzz 轴来看自 xxx 轴按逆时针方向转到有向线段 OPOPOP 的角，这里 PPP 为点 MMM 在 xOyxOyxOy 面上的投影（图 10-35）。这样的三个数 rrr、ϕ\phiϕ 和 θ\thetaθ 叫做点 MMM 的球面坐标，这里 rrr、ϕ\phiϕ 和 θ\thetaθ 的变化范围为

显然，点 MMM 的直角坐标与球面坐标的关系为

为了把三重积分中的变量从直角坐标变换为球面坐标，用三组坐标面 r=常数r = \text{常数}r=常数、ϕ=常数\phi = \text{常数}ϕ=常数、θ=常数\theta = \text{常数}θ=常数 把积分区域 Ω\OmegaΩ 分成许多小闭区域。考虑由 rrr、ϕ\phiϕ 和 θ\thetaθ 各取得微小增量 drdrdr、dϕd\phidϕ 和 dθd\thetadθ 所成的六面体的体积（图 10-36）。不计高阶无穷小，可把这个六面体看做长方体，其经线方向的长为 r dϕr \, d\phirdϕ、纬线方向的宽为 rsin⁡ϕ dθr \sin \phi \, d\thetarsinϕdθ、向径方向的高为 drdrdr，于是得

这就是球面坐标系中的体积元素。再注意到关系式（3-6），就有

要计算变量变换为球面坐标后的三重积分，可把它化为对 rrr、对 ϕ\phiϕ 及对 θ\thetaθ 的三次积分。

例4 求半径为 aaa 的球面与半顶角为 α\alphaα 的内接锥面所围成的立体（图 10-37）的体积。

解：设球面通过原点 OOO，球心在 zzz 轴上，又内接锥面的顶点在原点 OOO，其轴与 zzz 轴重合，则球面方程为 r=acos⁡ϕr = a \cos \phir=acosϕ，锥面方程为 ϕ=α\phi = \alphaϕ=α。因为立体所占有的空间闭区域 Ω\OmegaΩ 可用不等式

来表示，所以

计算得