机器学习-白板推导系列(十)-EM算法（Expectation Maximization）

10. EM算法（Expectation Maximization）

本章主要内容：

1. 凸集，凸函数，凹集，凹函数的概念
2. Jensen’s inequality
3. KL散度（相对熵）
4. EM算法两步迭代过程与收敛性证明
5. 广义EM算法与狭义EM算法

10.1 EM算法公式以及算法收敛性证明

$ExpectationMaximization(EM)$算法，中文名字叫做“期望最大”算法。是用来解决$具有隐变量的混合模型的高斯分布$。对于简单的问题，可以直接得出参数的解析解，比如：MLE(极大似然估计(例子)): $p(x|\theta )$。我们想要求解的结果就是：
$${\theta }_{MLE}=\arg \underset{\theta }{\max }\log p(x|\theta ).\text{\hspace{1em}(10.1.1)}$$
其中$\log p(x|\theta )$称为对数似然函数。一旦问题变得复杂，就不是这么简单了，特别是引入了隐变量之后，此时我们要用上EM算法（例子）。

10.1.1 EM算法简述

1. 假设有如下数据：

   • $X$:observed data
   • $Z$:unobserved data(latent variable)，分布为$q(z)$
   • $(X,Z)$:complete data
   • $\theta$:parameter

2. EM算法的目的是解决具有隐变量的参数估计（MLE、MAP）问题。因此对MLE引入隐变量得EM的基本表达式是：$${\theta }^{(t+1)}=arg\underset{\theta }{\max }{\int }_z\log p(x,z|\theta )\cdot p(z|x,{\theta }^{(t)})dz.\text{\hspace{1em}(10.1.2)}$$
   其中：

   • ${\theta }^{(t)}$表示$t$时刻的参数；
   • $p(z|x,{\theta }^{(t)})$是后验；
   • $\log p(x,z|\theta )$是完整数据，对数联合概率。

3. EM算法是一种迭代的算法，我们的目标是求：
   $$\begin{array}{lc}{\theta }^{(t+1)}& =\arg \underset{\theta }{\max }{\int }_{z}p(x,z|\theta )p(z|x,{\theta }^{(t)})dz\\ & =\arg \underset{\theta }{\max }{\mathbb{E}}_{z\sim p(z|x,{\theta }^{(t)})}[\log p(x,z|\theta )]\end{array}\text{\hspace{1em}(10.1.3)}$$
   EM算法的目标：找到一个更新的参数$\theta$，使得$\log p(x,z|\theta )$出现的概率更大。

4. $EM算法(公式(10.1.3))分为两步$：

   • 第一步是E：求出期望；

     固定${\theta }^{(t)}$，改变$q(z)$，使得$KL(q(z)||p(z|x,\theta ))=-{\int }_{z}q(z)log\frac{p(z|x,\theta )}{q(z)}\mathrm{d}z=0$，因此：$\log p(x|{\theta }^{(t)})={\int }_{z}q(z)log\frac{p(x,z|\theta )}{q(z)}\mathrm{d}z=ELBO.$

   • 第二步是M：将期望最大化。

     固定$q(z)$，极大化${\theta }^{(t+1)}=\arg \underset{\theta }{\max }{\mathbb{E}}_{z\sim P(z|x,{\theta }^{(t)})}\left[\log P(x,z|\theta )\right]$

   更深入的了解：EM算法的实例
   可以从下图理解：其中$F(...)$表示$lowbound$，为$ELBO$。
   

---

10.2 从ELBO+KL Divergence角度进行EM算法公式推导

10.2.1 概述

1. 回顾
   机器学习的模型实际上就可以看成是一堆的参数。极大似然估计的思想是求解：
   $${\theta }_{MLE}=\log P(x|\theta )\text{\hspace{1em}(10.2.1)}$$
   其中:

   • $X$为observed data；
   • $Z$为latent data，分布为$q(z)$；
   • $(X,Z)$为complete data；
   • $\theta$为parameter。

   对于$具有隐变量的混合模型的高斯分布$，EM公式就被我们描述为：
   $${\theta }^{(t+1)}=\arg \underset{\theta }{\max }{\int }_z\log P(x,z|\theta )P(z|x,{\theta }^{(t)})dz.\text{\hspace{1em}(10.2.2)}$$

2. EM算法的步骤
   EM算法可以被我们分解成E-step和M-step两个部分。

   • E(Expectation)-step：$P(z|x,{\theta }^{(t)})⟶{\mathbb{E}}_{z\sim P(z|x,{\theta }^{(t)})}\left[\log P(x,z|\theta )\right]$
   • M(Maximization)-step：${\theta }^{(t+1)}=\arg \underset{\theta }{\max }{\mathbb{E}}_{z\sim P(z|x,{\theta }^{(t)})}\left[\log P(x,z|\theta )\right]$
     上一章已经证明了EM算法的收敛性，即：
     $$\log P(x|{\theta }^{(t+1)})\ge \log P(x|{\theta }^{(t)})$$
     本节的目标就是推导EM算法公式(10.2.2)究竟是怎么来的。

10.2.2 从ELBO+KL散度的角度推到EM步骤

1. $E(Expectation)-step:KL=0,\log p(x|{\theta }^t)=ELBO$
   对$\log p(x|\theta )$进行处理：
   $$\begin{array}{rl}\log p(x|\theta )& =\log p(x,z|\theta )-\log p(z|x,\theta )\\ & =\log \frac{p(x,z|\theta )}{q(z)}-\log \frac{p(z|x,\theta )}{q(z)}(q(z)\ne 0).\end{array}\text{\hspace{1em}(10.2.3)}$$
   公式(10.2.3)引入一个关于$z的概率分布为q(z)$，然后式子两边同时求对$q(z)$的期望
   $$左边={\int }_{z}q(z)\cdot logp(x|\theta )\mathrm{d}z=logp(x|\theta ){\int }_{z}q(z)\mathrm{d}z=logp(x|\theta ).\text{\hspace{1em}(10.2.4)}$$
   $$右边=\underset{ELBO(evidencelowerbound)}{\underbrace{{\int }_{z}q(z)log\frac{p(x,z|\theta )}{q(z)}\mathrm{d}z}}\underset{KL(q(z)||p(z|x,\theta ))}{\underbrace{-{\int }_{z}q(z)log\frac{p(z|x,\theta )}{q(z)}\mathrm{d}z}}.\text{\hspace{1em}(10.2.5)}$$
   因此我们得出$logp(x|\theta )=ELBO+KL(q(z)||p(z|x,\theta ))$:

   • 由于KL散度恒$\ge 0$，因此$\log p(x|\theta )\ge ELBO$，则$ELBO就是似然函数\log p(x|\theta )的下界$。

   • 当$\log p(x|\theta )=ELBO$，就必须有$KL(q(z)||p(z|x,\theta ))=0$，根据 KL散度的定义, 也就是$q(z)=p(z|x,\theta )$。
     

   • 在每次迭代中取:
     $$q(z)=p(z|x,{\theta }^{(t)})\text{\hspace{1em}(10.2.6)}$$
     就可以保证$logp(x|{\theta }^t)$与$ELBO$相等。也就是当$\theta ={\theta }^{(t)}时，logp(x|{\theta }^t)$取$ELBO$:
     $$\begin{array}{rl}\log p(x|{\theta }^{(t)})& =\underset{ELBO}{\underbrace{{\int }_{z}p(z|x,{\theta }^{(t)})log\frac{p(x,z|{\theta }^{(t)})}{p(z|x,{\theta }^{(t)})}\mathrm{d}z}}\underset{=0}{\underbrace{-{\int }_{z}p(z|x,{\theta }^{(t)})log\frac{p(z|x,{\theta }^{(t)})}{p(z|x,{\theta }^{(t)})}\mathrm{d}z}}\\ & =ELBO\end{array}.\text{\hspace{1em}(10.2.7)}$$

2. $M(Maximization)-step:ELBO与\log p(x|\theta )$

   • 根据公式(10.2.7)可得：$logp(x|\theta )$与ELBO都是关于$\theta$的函数，且满足$logp(x|\theta )\ge ELBO$，也就是说$\log p(x|\theta )的图像总是在ELBO的图像的上面$。
   • 对于$q(z)$，我们取$q(z)=p(z|x,{\theta }^t)$，这也就保证了只有在$\theta ={\theta }^{(t)}时logp(x|\theta )$与$ELBO$才会相等，因此：$使ELBO取极大值的{\theta }^{(t+1)}一定能使得\log p(x|{\theta }^{(t+1)})\ge logp(x|{\theta }^{(t)})$。该过程如下图所示：
     
     通过上图，观察ELBO取极大值的过程：
     $$\begin{array}{ll}{\theta }^{(t+1)}& =\underset{\theta }{\mathrm{argmax}}ELBO=\underset{\theta }{\mathrm{argmax}}{\int }_{z}p(z|x,{\theta }^{(t)})log\frac{p(x,z|\theta )}{p(z|x,{\theta }^{(t)})}\mathrm{d}z\\ & =\underset{\theta }{\mathrm{argmax}}{\int }_{z}p(z|x,{\theta }^{(t)})logp(x,z|\theta )\mathrm{d}z-\underset{与\theta 无关}{\underbrace{\underset{\theta }{\mathrm{argmax}}{\int }_{z}p(z|x,{\theta }^{(t)})p(z|x,{\theta }^{(t)})\mathrm{d}z}}\\ & =\underset{\theta }{\mathrm{argmax}}{\int }_{z}p(z|x,{\theta }^{(t)})logp(x,z|\theta )\mathrm{d}z\\ & =\underset{\theta }{\mathrm{argmax}}{E}_{z|x,{\theta }^{(t)}}[logp(x,z|\theta )]\end{array}\text{\hspace{1em}(10.2.8)}$$
     其中${\theta }^{(t)}在每次\arg \underset{\theta }{\max }的时候是常量$，$\theta 才是变量$。因此：$EM算法的一个想法是让ELBO不断的增加，使\log P(X|\theta )不断变大$的一种攀爬的迭代方法。

---

10.3 从ELBO+Jensen不等式的角度推导EM算法

1. Jensen不等式
   对于一个凹函数$f(x)$，对于$t\in [0,1]$，存在$c=ta+(1-t)b,\varphi =tf(a)+(1-t)f(b)$。凹函数恒有$f(c)\ge \varphi$， 也就是：$$f(ta+(1-t)b)\ge tf(a)+(1-t)f(b).\text{\hspace{1em}(10.3.1)}$$
   
   如上图，当$t=\frac{1}{2}$时有$f(\frac{a}{2}+\frac{b}{2})\ge \frac{f(a)}{2}+\frac{f(b)}{2}$。 可以理解为：
   $$先求期望再求函数\underline{恒\ge }先求函数再求期望$$
   即函数值的期望大于等于期望的函数值：
   $$E[f(x)]\le f(E[x])\text{\hspace{1em}(10.3.2)}$$
2. $应用Jensen不等式导出EM算法$
   • $E(Expectation)-step:\log p(x|{\theta }^{(t)})=ELBO$：
     $$\begin{array}{rl}logp(x|\theta )& =log{\int }_{z}p(x,z|\theta )\mathrm{d}z=log{\int }_z\frac{p(x,z|\theta )}{q(z)}\cdot q(z)\mathrm{d}z\\ & =log{E}_{q(z)}[\frac{p(x,z|\theta )}{q(z)}]\ge \underset{ELBO}{\underbrace{E_{q(z)}[log\frac{p(x,z|\theta )}{q(z)}]}}\end{array}\text{\hspace{1em}(10.3.3)}$$
     根据$JensenInequality$的定义，当$\frac{P(x,z|\theta )}{q(z)}=C$时可以取得等号。

     此处的${\mathbb{E}}_{z\sim q(z)}\left[\log \frac{P(x,z|\theta )}{q(z)}\right]$是${\int }_{z}q(z)\log \frac{P(x,z|\theta )}{q(z)}dz$，也就是之前在KL Divergence角度进行分析时得到的ELBO(公式(10.2.6))。

   • $M(Maximization)-step:ELBO与\log p(x|\theta )$
     当取等时，可以达到最大，即：
     $$\begin{array}{rl}& \frac{p(x,z|\theta )}{q(z)}=C\\ \Rightarrow & q(z)=\frac{p(x,z|\theta )}{C}\\ \Rightarrow & {\int }_{z}q(z)\mathrm{d}z={\int }_z\frac{1}{C}p(x,z|\theta )\mathrm{d}z\\ \Rightarrow & 1=\frac{1}{C}{\int }_{z}p(x,z|\theta )\mathrm{d}z\\ \Rightarrow & C=p(x|\theta )\end{array}.\text{\hspace{1em}(10.3.4)}$$
     将$C$代入$q(z)=\frac{p(x,z|\theta )}{C}$得:
     $$q(z)=\frac{p(x,z|\theta )}{p(x|\theta )}=p(z|x,\theta ).\text{\hspace{1em}(10.3.5)}$$
     $q(z)$就是后验概率，当$q(z)=p(z|x|\theta )$时取等号时：
     $$logp(x|\theta )=\underset{ELBO}{\underbrace{E_{q(z)}[log\frac{p(x,z|\theta )}{q(z)}]}}.\text{\hspace{1em}(10.3.6)}$$
     因此在迭代更新过程中取$q(z)=p(z|x,{\theta }^t)$。接下来的推导如公式(10.2.7)和公式(10.2.8)，最终得到：
     $${\theta }^{(t+1)}=arg\underset{\theta }{\max }{\int }_z\log P(x,z|\theta )\cdot P(z|x,{\theta }^{(t)})dz.\text{\hspace{1em}(10.3.7)}$$

---

总结

最后梳理一下EM算法的实现思想。我们的目标是使$P(X|\theta )$似然函数值最大。但是，直接优化非常的难。所以需要优化下降的方法。对于，每一个${\theta }^{(t)}$时，计算得到下界为：${\mathbb{E}}_{Z\sim Q(Z)}\left[\log \frac{P(X,Z|\theta )}{P(Z|X,{\theta }^{(t)})}\right]$，令这个值最大就得到了想要求得的${\theta }^{(t+1)}$。然后，按这个思路，不断的进行迭代。

EM算法的步骤
EM算法可以被我们分解成E-step和M-step两个部分。

• $输入$：
  观察到的数据$x=(x_1,x_2,...x_n)$，联合分布函数$p(x,z;\theta )$，条件分布$p(z|x,\theta )$，最大迭代次数J。
• $算法步骤$：
  1. 随机初始化模型参数$\theta$的初值${\theta }_0$。
  2. $j=1,2,...,J$ 开始EM算法迭代。
  3. E(Expectation)-step($P(z|x,{\theta }^{(t)})⟶{\mathbb{E}}_{z\sim P(z|x,{\theta }^{(t)})}\left[\log P(x,z|\theta )\right]$)
     计算联合分布的条件概率期望：
     • $q_i(z_i)=p(z_i|x_i,{\theta }_j)$
     • $ELBO(\theta ,{\theta }_j)={\mathbb{E}}_{z\sim P(z|x,{\theta }^{(t)})}\left[\log P(x,z|\theta )\right]={\sum }_{i=1}^n{\sum }_{z_i}^{}{q}_i(z_i)log\frac{p(x_i,z_i;\theta )}{q_i(z_i)}$
  4. M(Maximization)-step：${\theta }^{(t+1)}=\arg \underset{\theta }{\max }{\mathbb{E}}_{z\sim P(z|x,{\theta }^{(t)})}\left[\log P(x,z|\theta )\right]$
     极大化ELBO，得到${\theta }_{j+1}$:
     • ${\theta }^{(t+1)}=\arg \underset{\theta }{\max }{\mathbb{E}}_{z\sim P(z|x,{\theta }^{(t)})}\left[\log P(x,z|\theta )\right]$
  5. 如果${\theta }_{j+1}$已经收敛，则算法结束。否则继续进行E步和M步进行迭代。
• $输出$： 模型参数$\theta$。
  

---

10.4 EM算法的收敛性

EM算法的求解过程是${\theta }^{(t)}⟶{\theta }^{(t+1)}$，因此迭代是：$\log P(x|{\theta }^{(t)})\to \log P(x|{\theta }^{(t+1)})$，若要收敛，则需要证明$P(x|{\theta }^{(t)})\le P(x|{\theta }^{(t+1)})$。证明如下：

1. $引出不等式$
   对$P(x|\theta )$加入隐变量，,利用全概率公式（$P(A,B)=P(B|A)P(A)$）可以写成：
   $$\log P(x|\theta )=\log \frac{P(x,z|\theta )}{P(z|x,\theta )}=\log P(x,z|\theta )-\log P(z|x,\theta ).\text{\hspace{1em}(10.1.4)}$$
   接下来在公式两边同时求关于$P(z|x,{\theta }^{(t)})$的期望：

   • 左边
     $$\begin{array}{ll}左边& ={\int }_{z}P(z|x,{\theta }^{(t)})\cdot \log P(x|\theta )dz\\ & =\log P(x|\theta ){\int }_{z}P(z|x,{\theta }^{(t)})dz\\ & =\log P(x|\theta ).\end{array}\text{\hspace{1em}(10.1.5)}$$
   • 右边
     $$\begin{array}{lc}右边& =\underset{Q(\theta ,{\theta }^{(t)})}{\underbrace{{\int }_{z}P(z|x,{\theta }^{(t)})\cdot \log P(x,z|\theta )dz}}-\underset{H(\theta ,{\theta }^{(t)})}{\underbrace{{\int }_{z}P(z|x,{\theta }^{(t)})\cdot \log P(z|x,\theta )dz}}\end{array}.\text{\hspace{1em}(10.1.6)}$$
     因此证明$\log P(x|{\theta }^{(t)})\le \log P(x|{\theta }^{(t+1)})$：
     $$logP(x|{\theta }^{(t)})-logP(x|{\theta }^{(t+1)})=[Q({\theta }^{(t)},{\theta }^{(t)})-Q({\theta }^{(t+1)},{\theta }^{(t)})]-[H({\theta }^{(t)},{\theta }^{(t)})-H({\theta }^{(t+1)},{\theta }^{(t)})]\le 0$$
     相当于证明：
     $$Q({\theta }^{(t)},{\theta }^{(t)})-H({\theta }^{(t)},{\theta }^{(t)})\le Q({\theta }^{(t+1)},{\theta }^{(t)})-H({\theta }^{(t+1)},{\theta }^{(t)}).\text{\hspace{1em}(10.1.7)}$$

2. $证明Q({\theta }^{(t+1)},{\theta }^{(t)})\ge Q({\theta }^{(t)},{\theta }^{(t)})$
   写出$Q({\theta }^{(t)},{\theta }^{(t)})$和$Q({\theta }^{(t+1)},{\theta }^{(t)})$的形式：
   $$\begin{gathered} Q({\theta }^{(t)},{\theta }^{(t)})={\int }_{z}P(z|x,{\theta }^{(t)})\cdot \log P(x,z|{\theta }^{(t)})dz \\ Q({\theta }^{(t+1)},{\theta }^{(t)})={\int }_{z}P(z|x,{\theta }^{(t)})\cdot \log P(x,z|{\theta }^{(t+1)})dz.\text{\hspace{1em}(10.1.8)} \end{gathered}$$
   根据EM算法的定义：
   $${\theta }^{(t+1)}=arg\underset{\theta }{\max }{\int }_z\log P(x,z|\theta )\cdot P(z|x,{\theta }^{(t)})dz$$
   所以很明显：
   $$Q({\theta }^{(t+1)},{\theta }^{(t)})\ge Q({\theta }^{(t)},{\theta }^{(t)}).\text{\hspace{1em}(10.1.9)}$$

3. $证明H({\theta }^{(t+1)},{\theta }^{(t)})\le H({\theta }^{(t)},{\theta }^{(t)})$
   根据$Q$ 的结论，接下来需要证明 $H({\theta }^{(t+1)},{\theta }^{(t)})\le H({\theta }^{(t)},{\theta }^{(t)})$
   $$\begin{array}{ll}& H({\theta }^{(t+1)},{\theta }^{(t)})-H({\theta }^{(t)},{\theta }^{(t)})\\ & ={\int }_{z}P(z|x,{\theta }^{(t)})\cdot \log P(z|x,{\theta }^{(t+1)})dz-{\int }_{z}P(z|x,{\theta }^{(t)})\cdot \log P(z|x,{\theta }^{(t)})dz\\ & ={\int }_{z}P(z|x,{\theta }^{(t)})\cdot [\log P(z|x,{\theta }^{(t+1)})-\log P(z|x,{\theta }^{(t)})]dz\\ & ={\int }_{z}P(z|x,{\theta }^{(t)})\cdot \log \frac{P(z|x,{\theta }^{(t+1)})}{P(z|x,{\theta }^{(t)})}dz\end{array}$$

   • $利用KLDivergence来证明$：
     $KLDivergence$的定义：两个概率分布$P(x)$和$Q(x)$的$KL散度$的定义为$$D_{KL}(P||Q)=E_{x\sim P}[log\frac{P(x)}{Q(x)}].\text{\hspace{1em}(10.1.10)}$$
     因为KL散度是恒$\ge 0$的，则：
     $${\int }_{z}P(z|x,{\theta }^{(t)})\cdot \log \frac{P(z|x,{\theta }^{(t+1)})}{P(z|x,{\theta }^{(t)})}dz=-KL(P(z|x,{\theta }^{(t)})\Vert P(z|x,{\theta }^{(t+1)}))<0\text{\hspace{1em}(10.1.11)}$$
     所以$H({\theta }^{(t+1)},{\theta }^{(t)})\le H({\theta }^{(t)},{\theta }^{(t)})$。
   • $利用Jensen不等式来证明$：
     $Jensen不等式$的定义：若 $f(x)$是convex function(凸函数) 则
     $$E[f(x)]\ge f(E[x]).\text{\hspace{1em}(10.1.12)}$$
     
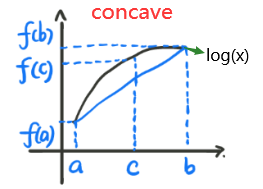
     由于$log(x)$为concave function（凹函数），则
     $$E[\log x]\le \log E[x].\text{\hspace{1em}(10.1.13)}$$
     因此：
     $$\begin{array}{ll}& H({\theta }^{(t+1)},{\theta }^{(t)})-H({\theta }^{(t)},{\theta }^{(t)})\\ & ={\int }_{z}P(z|x,{\theta }^{(t)})\cdot \log \frac{P(z|x,{\theta }^{(t+1)})}{P(z|x,{\theta }^{(t)})}dz\\ & \le \log {\int }_{z}P(z|x,{\theta }^{(t)})\cdot \frac{P(z|x,{\theta }^{(t+1)})}{P(z|x,{\theta }^{(t)})}dz\\ & =\log {\int }_{z}P(z|x,{\theta }^{(t+1)})dz\\ & =\log 1=0\end{array}$$
     所以$H({\theta }^{(t+1)},{\theta }^{(t)})\le H({\theta }^{(t)},{\theta }^{(t)})$。

   由$KLDivergence$和$Jensen不等式$可知：
   $$H({\theta }^{(t+1)},{\theta }^{(t)})-H({\theta }^{(t)},{\theta }^{(t)})\le 0.\text{\hspace{1em}(10.1.14)}$$

   根据公式(10.1.9)和公式（10.1.14）可得：
   $$Q({\theta }^{(t)},{\theta }^{(t)})-H({\theta }^{(t)},{\theta }^{(t)})\le Q({\theta }^{(t+1)},{\theta }^{(t)})-H({\theta }^{(t+1)},{\theta }^{(t)})\text{\hspace{1em}(10.1.7)}$$
   则EM算法的收敛性：
   $$\log P(x|{\theta }^{(t)})\le \log P(x|{\theta }^{(t+1)}).\text{\hspace{1em}(10.1.15)}$$
   证毕。

4. 其他定理
   另外还有其他定理保证了EM的算法收敛性。首先对于${\theta }^{(i)}(i=1,2,\cdots )$序列和其对应的对数似然序列$L({\theta }^{(t)})=logp(x|{\theta }^{(t)})(t=1,2,\cdots )$有如下定理：

   • 如果$p(x|\theta )$有上界，则$L({\theta }^{(t)})=logp(x|{\theta }^{(t)})$收敛到某一值$L^{\ast }$；
   • 在函数$Q(\theta ,{\theta }^{{}^{\prime }})$与$L(\theta )$满足一定条件下，由EM算法得到的参数估计序列${\theta }^{(t)}$的收敛值${\theta }^{\ast }$是$L(\theta )$的稳定点。

---

10.5 再回首

接下来的内容是：

• 从狭义的EM推广到广义的EM
• 证明狭义EM是EM的一个特例
• 介绍真正的EM

本节主要介绍EM算法的由来。

1. $EM是一种算法，不是模型$，有点像梯度下降（GD）。
2. $EM主要是为了解决生成模型，并且是概率生成模型$。

   • 假设有以下数据：

     • $X$：Observed Variable $⟶$ X = { x i } i = 1 N X=\{ x_i \}_{i=1}^N X={xi​}i=1N​；
     • $Z$：Latent Variable $⟶$ Z = { Z i } i = 1 N Z=\{ Z_i \}_{i=1}^N Z={Zi​}i=1N​；
     • $(X,Z)$：Complete Model；
     • $\theta$：Model Parameter。

     EM算法的目标是得到一个参数$\hat{\theta }$，来推导出$X$，也就是$P(X|\theta )$。实际上是假设使用MLE：
     $$\begin{array}{ll}\hat{\theta }& =\arg {\max }_{\theta }P(X|\theta )\\ & =\arg {\max }_{\theta }{\prod }_{i=1}^{N}P(x_i|\theta )\\ & =\arg {\max }_{\theta }{\sum }_{i=1}^N\log P(x_i|\theta )\end{array}\text{\hspace{1em}(10.4.1)}$$

   • 实际观察的输入空间$\mathcal{X}$分布$P(X)$是非常复杂。可能什么规律都找不出来，这时引入了一个隐变量$Z$，这个变量中包含了已有的一些归纳总结，引入了内部结构。假设存在一个隐变量$z$能够生成$x$。即：
     $$P(x)={\int }_{z}P(x,z)dz.\text{\hspace{1em}(10.4.2)}$$

---

10.6 广义EM

1. EM算法是为了解决参数估计问题，也就是learning问题：
   $$\hat{\theta }=\arg \underset{\theta }{\max }P(x|\theta ).\text{\hspace{1em}(10.5.1)}$$
   $P(x|\theta )$可能会非常的复杂。在生成模型的思路中，假设一个隐变量$Z$。有了这个生成模型的假设后，就可以引入一些潜在归纳出的结构进去。通过$P(x)=\frac{P(x,z)}{P(z|x)}$，就可以把问题具体化了。

这里说明一下，我们习惯用的表达是$\log P(x|\theta )$，但是也有的文献中使用$P(x;\theta )$或者$P_{\theta }(x)$。这三种表达方式代表的意义是等价的。

2. 引出隐变量
   把隐变量$q(z)（q(z)\ne 0）$代入：
   $$logp(x|\theta )={\int }_{z}q(z)log\frac{p(x,z|\theta )}{q(z)}\mathrm{d}z-{\int }_{z}q(z)log\frac{p(z|x,\theta )}{q(z)}\mathrm{d}z=ELBO+KL(q||p).\text{\hspace{1em}(10.5.1)}$$
   其中$q=q(z),p=p(z|x,\theta )$：
   $$\{\begin{array}{l}ELBO=L(q,\theta )=E_{q(z)}[\log \frac{P(x,z|\theta )}{q(z)}]\\ KL(q\Vert p)=\int q(z)\cdot \log \frac{q(z)}{P(z|x,\theta )}dz\end{array}.\text{\hspace{1em}(10.5.2)}$$
   因为$KL\ge 0$，所以 $\log P(x|\theta )\ge L(q,\theta )$；当$q=p$时，$KL=0$。

3. 求解$p$和$\theta$
   在10.2节中假定$q(z)=P(z|x,\theta )$ ，但实际上$P(z|x,{\theta }^{(t)})是intractable$的，如果生成模型较复杂，则无法求出$P(z|x,{\theta }^{(t)})$。因此$q$无法直接取到$p$ ，需要进行优化，逐渐接近 $p$。

   • 先固定$\theta$
     固定的$\theta$，$q$越接近$p$，则$KL(q||p)$越小，由于$\log P(x|\theta )$不变，所以$ELBO$将越大。此时，就要求$q$的最大值：
     $$\hat{q}=arg\underset{q}{\min }KL(q\Vert p)=arg\underset{q}{\max }L(q,\theta ).\text{\hspace{1em}(10.5.3)}$$
   • 再固定$q$
     当$q$被我们求出来以后，我们就可以将$q$固定了，再来求解$\theta$：
     $$\hat{\theta }=\arg \underset{\theta }{\max }L(\hat{q},\theta ).\text{\hspace{1em}(10.5.4)}$$

   $广义的EM算法基本思路$：
   $$\begin{gathered} E-step：q^{(t+1)}=\underset{q}{\mathrm{argmax}}L(q,{\theta }^{(t)}) \\ M-step：{\theta }^{(t+1)}=\underset{q}{\mathrm{argmax}}L(q^{(t+1)},\theta ).\text{\hspace{1em}(10.5.5)} \end{gathered}$$

4. 注
   再次观察一下ELBO：
   $$\begin{array}{ll}ELBO=L(q,\theta )& =E_{q(z)}[\log \frac{P(x,z|\theta )}{q(z)}]\\ & =E_q[\log P(x,z)-\log q(z)]\\ & =E_q[\log P(x,z)]-E_q[\log q(z)]\\ & =E_q[\log P(x,z)]+H[q(z)]\end{array}\text{\hspace{1em}(10.5.6)}$$
   $${\theta }^{(t+1)}=arg\underset{\theta }{\max }{E}_{p(z|x,{\theta }^{(t)})}[\log P(x,z|\theta )]\text{\hspace{1em}(10.5.7)}$$
   公式(10.5.7)是之前讲的狭义EM算法的M-step，对比公式(10.5.7)和公式(10.5.6)（广义EM算法的M-Step），会发现ELBO中最后那个$H(q(z))$竟然不见了。这是为什么？因为在M-step中，$q(z)已经是假设固定了，显然H[q(z)]就是一个定值$，并且与优化目标$\theta$之间并没有关系，所以就被省略掉了。

   • $广义的EM算法$：
     $$\begin{array}{rl}E-step& ：q^{(t+1)}=\underset{q}{\mathrm{argmax}}L(q,{\theta }^{(t)})\\ M-step& ：{\theta }^{(t+1)}=\underset{q}{\mathrm{argmax}}L(q^{(t+1)},\theta )\end{array}\text{\hspace{1em}(10.5.8)}$$
   • $狭义的EM算法$：
     $$\begin{array}{rl}E-step& ：P(z|x,{\theta }^{(t)})⟶{\mathbb{E}}_{z\sim P(z|x,{\theta }^{(t)})}\left[\log P(x,z|\theta )\right]\\ M-step& ：{\theta }^{(t+1)}=\arg \underset{\theta }{\max }{\mathbb{E}}_{z\sim P(z|x,{\theta }^{(t)})}\left[\log P(x,z|\theta )\right]\end{array}\text{\hspace{1em}(10.5.9)}$$
     $两者的差异$：狭义EM算法是广义EM算法的特例——狭义EM算法直接令$q(z)=p(z|x,\theta )$，当然这种情况下$p(z|x,\theta )$是可求解的，这时只需要求解$\theta$。对于广义EM算法，$p(z|x,\theta )$是不可求解的，因此需要求解$\theta$和$q(z)$，当$q(z)$确定后信息熵$H[q(z)]$就随之确定。

---

10.7 EM的变种

1. SMO与GD
   上节推广出广义EM算法：
   $$\begin{array}{rl}E-step& ：q^{(t+1)}=\underset{q}{\mathrm{argmax}}L(q,{\theta }^{(t)})\\ M-step& ：{\theta }^{(t+1)}=\underset{q}{\mathrm{argmax}}L(q^{(t+1)},\theta ).\end{array}\text{\hspace{1em}(10.6.1)}$$
   • 因为$两步都是max$，所以也称为MM算法。
   • 这两步方法也是$坐标上升法$（SMO，固定部分坐标，优化其他坐标，再⼀遍⼀遍的迭代）。

     SMO算法采用的也是坐标上升法。

   • 梯度下降法(SG)与坐标上升法（SMO).
     
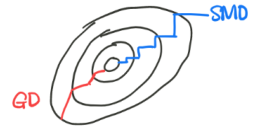
     坐标上升法的优化方向基本是恒定不变的，而梯度下降法的优化方向是随着梯度方向而不断发生改变的。
2. EM算法的变形
   如果在 EM 框架中，⽆法求解$z$后验概率，那么需要采⽤⼀些变种的 EM 来估算这个后验：
   1. 如果E-Step采用$基于平均场的VI$，则称为VBEM/VEM；
   2. 采用$蒙特卡洛采样法$求后验，称为：基于蒙特卡洛的EM（MCEM）。