台湾国立大学机器学习技法.听课笔记(第六讲)
:Support Vector Regression
一,Kernel Ridge Regression
1.提出线性岭回归问题
我们上一讲学习了解决Two-level的问题时,我们可以用两种方法解决:

那么ridge regression有啥特点呢?
那我们有没有什么方法能解决linear/ridge regression(线性岭回归)呢??
2,提出kernel Ridge Regression Problem问题
所以kernel Ridge Regression Problem的模型是:
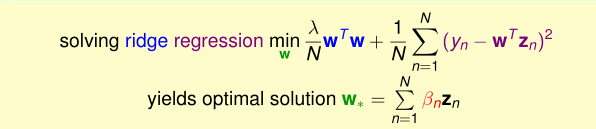
我们用上一讲中的Representer theorem的方法带入,就得到:
现在我们就是解无约束的优化问题:

我们把已经解决了的问题与已有的线性问题进行对比,可以得到:
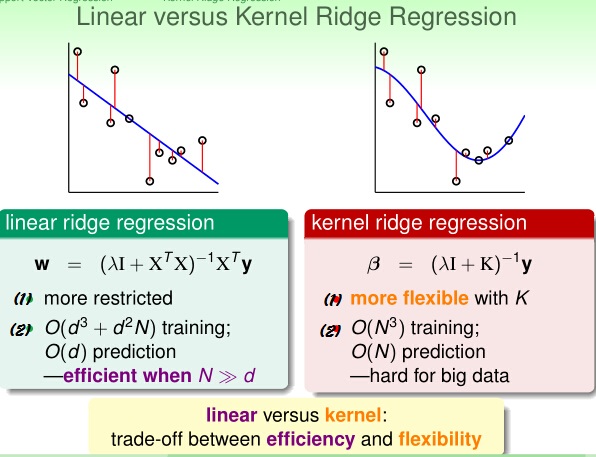
二,Support Vector Regression Primal
我们先对SVM的最小二乘问题进行定义:
那我们来看看LSSVM的特点:
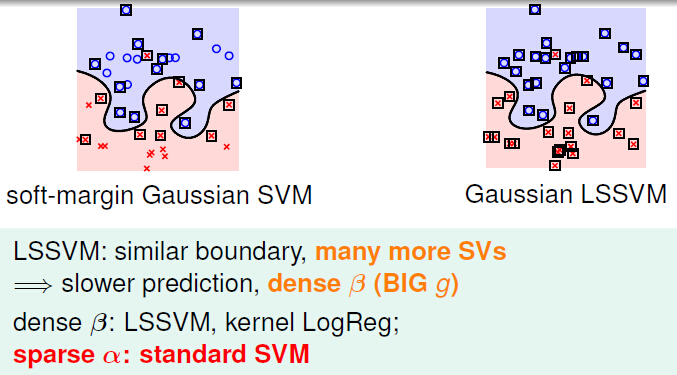
那我们能不能用LSSVM得到sparse的β呢??
1.tube Regression
我们通过tube Regression得到得到sparse β:

TUBE Regression它有啥特点呢?如果你选择的参数够好,他其实和square有点相像:
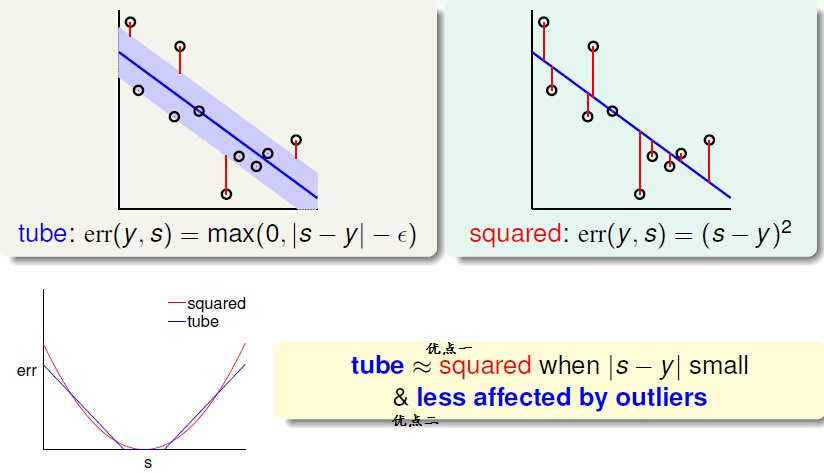
于是我们通过化简和简化,就得到了TuBe Regression 的一般表示形式:
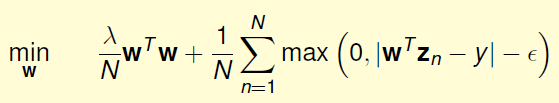
2,Support Vector Regression(SVR)
对其与标准的SVM格式进行对比,得到:

我们把上式称为Support Vector Regression(SVR),得到SVR问题的特点是,参数时表示什么形式呢?

三,Support Vector Regression Dual
我们已经把SVR已经写成了QP问题的基本形式,那我们能不能用Lagrange Dual问题呢?
我们先把SVR问题写成Lagrange 问题。
于是SVR问题变成了无约束的Lagrange问题,运用Lagrange Dual形式,导出其KKT条件的形式(具体形式见我们推到见Lecture 4):

我们对KKT田间得出来的等式或者complementary slackness进行分析:

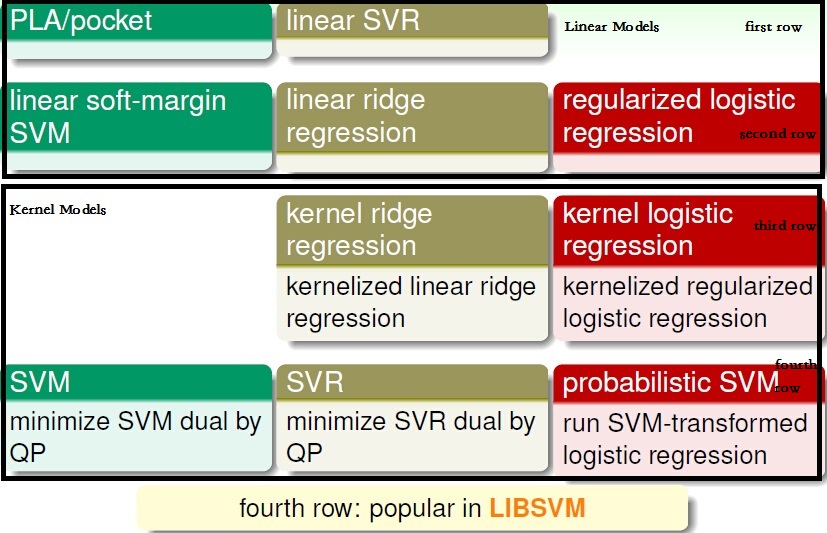
四,Summary of Kernel Models
1, Linear Model
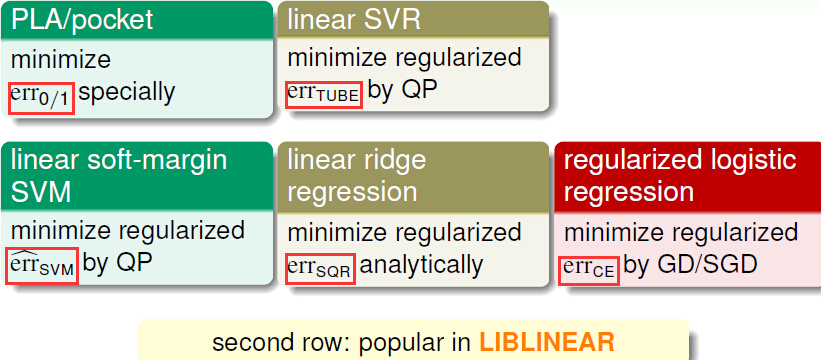
我们在机器学习基石上已经学习了PLC/Pocket,Linear ridge regression,regularizedlogistics regression;后来我们在机器学习技法学到了linear soft-margin SVM和linear SVR。这些都是我们至今学习到的linear Models。
2,Linear/Kernel Models
我们再对SVM进行Dual,得到Dual SVM—SVM with kernel;对SVR进行Dual,得到Dual SVR—SVR with kernel;对Linear ridge regression进行Dual,得到kernel ridge regression;对regularized Logistic Regression进行Dual,得到Kernel Logistic regression。
3,kernel 的选择

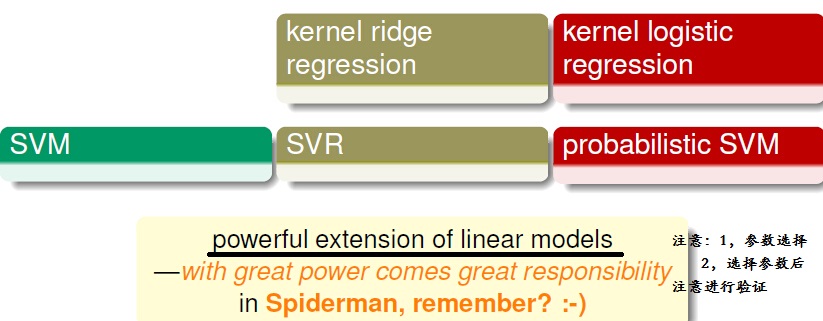
总结:
我们现在已经学到kernel Models的选择,我们下一讲开始说模型的选择。












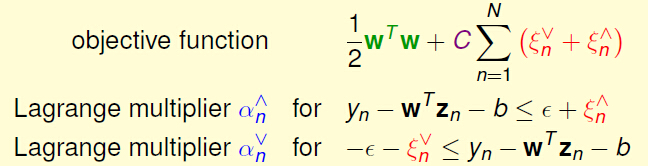

















 5304
5304

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








