本次分享主要是对相机标定原理做一个简介,让初学者对相机标定有一个简单的认识,对于具有资深标定经验的人员可能会稍显简单,本文主要分为以下5个部分:
-
相机模型
- 小孔成像
- 坐标系
- 相机畸变
- 内参&外参
-
张正友标定法
- 张正友标定原理
-
改进方法
- 圆环&棋盘格
- 偏心误差
-
标定实操
- opencv标定函数
- 相机机位和数量选择
- 标定结果的评判标准
- 应用
- 单目:PnP问题
- 双目测量
-
经验分享
- 为何要用背光板
- 标定特征点个数选取
1、相机模型
首先简单介绍一下相机成像原理:
1.1 小孔成像
相机成像模型是小孔成像,它的原理是光在同种均匀介质中,在不受引力作用干扰的情况下沿直线传播。小孔成像特点是光的直线传播,各种颜色的光都能通过小孔后成像。
- 小孔成像时,像的清晰程度与小孔的大小有关、跟小孔的形状无关。
- 小孔成像的小孔越小,成像越清晰,但是亮度会比较小;
- 小孔成像是倒立、放大;
- 小孔成像成的是倒立的实像, 这是因为光线在通过小孔时会发生折射和散射,从而导致图像的方向发生了变化。

(1)世界坐标系:代表物体再真实世界里的三维坐标,坐标系用
X
w
X_w
Xw,
Y
w
Y_w
Yw,
Z
w
Z_w
Zw表示,如图1。
(2)相机坐标系:代表以相机光学中心为原点的坐标系,光轴与
z
z
z轴重合,坐标系用
X
c
X_c
Xc,
Y
c
Y_c
Yc,
Z
c
Z_c
Zc表示,如图2。
(3)图像坐标系:代表相机拍摄图像的坐标系,原点为相机光轴与成像平面的交点,是图像的中心点,坐标系用
X
X
X,
Y
Y
Y表示,如图3左图。
(4)像素坐标系:由于图像的基本单位是像素,所以该坐标系是图像上点在图像存储矩阵中的像素位置,坐标原点在左上角,坐标系用
u
u
u,
v
v
v表示,如图3右图。
注意:前三个坐标系的单位是
m
m
(
毫米
)
,而最后一个坐标系的单位是
p
i
x
e
l
(
像素
)
。
\color {red}{注意:前三个坐标系的单位是mm(毫米),而最后一个坐标系的单位是pixel(像素)。}
注意:前三个坐标系的单位是mm(毫米),而最后一个坐标系的单位是pixel(像素)。

O w O_w Ow为坐标原点,世界坐标系是由用户定义的三维世界坐标系,描述物体和相机在真实世界中的位置,坐标原点 O w O_w Ow可以任意选择。

相机坐标系,以相机的光心
S
S
S 为坐标原点,
X
c
X_c
Xc 轴 和
Y
c
Y_c
Yc 轴平行于图像坐标系的
x
x
x 轴和
y
y
y 轴,
Z
c
Z_c
Zc 轴为相机的光轴(因为
Z
c
Z_c
Zc 与相机的光轴重合),图中的矩形区域代表的是相机的物理成像平面。
如上图2,假设图1世界坐标系下的某一三维点
P
w
(
X
w
,
Y
w
,
Z
w
)
P_w(X_w,Y_w,Z_w)
Pw(Xw,Yw,Zw) 投影到相机坐标系下的三维坐标是
P
c
(
X
c
,
Y
c
,
Z
c
)
P_c(X_c,Y_c,Z_c)
Pc(Xc,Yc,Zc) ,再由相机坐标系投影到图像坐标系下的二维坐标是
P
(
w
,
y
)
P(w,y)
P(w,y) 。

图像坐标系:与物理成像平面重合,以物理成像平面的中心(相机光轴
z
\bf z
z 与成像平面的交点)
O
′
\bf O^{'}
O′ 为坐标原点,
x
′
\bf x^{'}
x′ 轴和
y
′
\bf y^{'}
y′ 轴 分别平行于物理成像平面的两条边。
像素坐标系:与物理成像平面重合,以物理成像平面的左上角顶点为原点,
u
\bf u
u 轴和
v
\bf v
v 轴分别平行于图像坐标系的
x
′
\bf x^{'}
x′ 轴和
y
′
\bf y^{'}
y′ 轴。
为了得到真实世界里物体的图像,需要将真实世界的物体映射到像素坐标下,所以相机成像 \bf\color {red} {为了得到真实世界里物体的图像,需要将真实世界的物体映射到像素坐标下,所以相机成像} 为了得到真实世界里物体的图像,需要将真实世界的物体映射到像素坐标下,所以相机成像
的过程就是,世界坐标到像素坐标的映射过程: \bf\color {red} {的过程就是,世界坐标到像素坐标的映射过程:} 的过程就是,世界坐标到像素坐标的映射过程:
即世界坐标系 − > 相机坐标系 − > 图像坐标系 − > 像素坐标系。 \bf\color {red} {即世界坐标系->相机坐标系->图像坐标系->像素坐标系。} 即世界坐标系−>相机坐标系−>图像坐标系−>像素坐标系。
1.2.1 世界坐标系到相机坐标系的变换:
世界坐标系是真实世界的基准坐标系,在三维空间中,物体的运动可以分为两种:刚体运动和非刚体运动。
- 刚体运动是指物体的每一点在运动过程中都保持相对位置不变,包括平移和旋转运动;
- 非刚体运动则是指物体在运动过程中发生了形状的变化,比如拉伸、挤压、弯曲等;
针对相机来说,我们需要知道真实世界的物体在相机坐标系下的位置,这个坐标的转换过程是一个刚体变换的过程,而刚体从世界坐标系转换到相机坐标系的过程,又可以通过旋转和平移这两个基础运动来得到,因此我们将其变换过程,由一个旋转矩阵和平移向量组合成的齐次坐标矩阵来表示:
对于一个刚体变换,可以表示为:
[ X c Y c Z c 1 ] = [ R t 0 1 ] [ X w Y w Z w 1 ] (0) \begin{bmatrix} X_c \\ Y_c \\ Z_c \\ 1 \end{bmatrix}=\begin{bmatrix} R & t \\ 0 & 1 \\ \end{bmatrix}\begin{bmatrix} X_w \\ Y_w \\ Z_w \\ 1 \end{bmatrix} \tag{0} XcYcZc1 =[R0t1] XwYwZw1 (0)
其中
[
R
t
0
1
]
=
[
R
3
×
3
t
3
×
1
0
1
]
(1)
\begin{bmatrix} R^{} & t^{} \\ 0 & 1 \\ \end{bmatrix} = \begin{bmatrix} R^{3\times3} & t^{3\times1} \\ 0 & 1 \\ \end{bmatrix} \tag{1}
[R0t1]=[R3×30t3×11](1)
- 坐标转换矩阵(3维到3维):
- R R R是一个 3 ∗ 3 3*3 3∗3的旋转矩阵,因为坐标系是3个维度,每个维度又有3个自由度,这是由于旋转运动可向3个方向进行旋转;
- t t t是一个 3 ∗ 1 3*1 3∗1的平移矩阵,因为坐标系是3个维度,每个维度只有1个自由度,这是由于平移运动只能向一个方向进行平移;
- 由一个旋转矩阵和一个平移矩阵,可唯一确定一个刚体变换。
1.2.2 相机坐标系到图像坐标系的变换:
该变换可以看作是简单的射影变换(将相机看作小孔成像模型),将三维坐标变换为二维坐标。其中
f
f
f为相机的焦距(焦距
f
f
f 在相机出厂时即可获得)。
{
x
=
f
Z
c
X
c
y
=
f
Z
c
Y
c
(2)
\begin{cases} x=\dfrac{f}{Z_c}X_c \\ \\ y=\dfrac{f}{Z_c}Y_c \\ \tag{2} \end{cases}
⎩
⎨
⎧x=ZcfXcy=ZcfYc(2)
用矩阵表示
[
x
y
1
]
=
[
f
/
Z
c
0
0
0
0
f
/
Z
c
0
0
0
0
1
/
Z
c
0
]
[
X
c
Y
c
Z
c
1
]
(3)
\begin{bmatrix} x \\ y \\ 1 \end{bmatrix}=\begin{bmatrix} f/Z_c & 0 & 0 & 0 \\ 0 & f/Z_c & 0 & 0 \\ 0 & 0 & 1/Z_c & 0 \\ \end{bmatrix}\begin{bmatrix} X_c \\ Y_c \\ Z_c \\ 1 \end{bmatrix} \tag{3}
xy1
=
f/Zc000f/Zc0001/Zc000
XcYcZc1
(3)
- Z c Z_c Zc即为图3右图中相似三角形的 Z Z Z;
- 中间的矩阵即为坐标转换矩阵(3维到2维)。
1.2.3 图像坐标系到像素坐标系的变换:
假设图像 x 方向每毫米有
f
x
f_x
fx个像素,y 方向每毫米有
f
y
f_y
fy个像素,则有:
{
u
=
c
x
+
x
⋅
f
x
v
=
c
y
+
y
⋅
f
y
(4)
\begin{cases} u=c_x+x \cdot{f_x} \\ \\ v=c_y+y \cdot{f_y} \\ \tag{4} \end{cases}
⎩
⎨
⎧u=cx+x⋅fxv=cy+y⋅fy(4)
用矩阵表示
[
u
v
1
]
=
[
f
x
0
c
x
0
f
y
c
y
0
0
1
]
[
x
y
1
]
(5)
\begin{bmatrix} u \\ v \\ 1 \end{bmatrix}=\begin{bmatrix} f_x & 0 & c_x \\ 0 & f_y& c_y \\ 0 & 0 & 1 \\ \end{bmatrix}\begin{bmatrix} x \\ y \\ 1 \end{bmatrix} \tag{5}
uv1
=
fx000fy0cxcy1
xy1
(5)
- 其中 c x c_x cx, c x c_x cx是图像坐标系原点在像素坐标系下的坐标;
- 中间的矩阵即为坐标转换矩阵(2维到2维)。
根据上述坐标转换可以看出,从世界坐标系,经过三次矩阵的连乘,就可以把世界坐标系下的一个3维的点转换为像素坐标系下的一个2维的像素。这个根据矩阵变换算出像素坐标,是理想状态下的映射坐标,没有产生任何的畸变情况,但是在相机实际拍摄过程中,由于硬件等原因,或多或少会产生图像畸变。
1.3 相机畸变
相机拍摄的图像一般是存在畸变的,比如鱼眼镜头的畸变是比较严重的,正常的一个3维物体,假如说它是横平竖直的一个物体,由于畸变的存在,它在相机里的成像是会产生一些弯曲,一般会有下面两种弯曲情况,正常情况下我们只考虑 径向畸变 和 切向畸变。
对于相机畸变模型,在数学表示上就是一个多项式的表示:
{
x
d
i
s
t
o
r
t
e
d
=
x
(
1
+
k
1
r
2
+
k
2
r
4
+
k
3
r
6
)
+
2
p
1
x
y
+
p
2
(
r
2
+
2
x
2
)
y
d
i
s
t
o
r
t
e
d
=
y
(
1
+
k
1
r
2
+
k
2
r
4
+
k
3
r
6
)
+
2
p
2
x
y
+
p
1
(
r
2
+
2
y
2
)
(6)
\begin{cases} x_{distorted}=x(1+k_1r^2+k_2r^4+k_3r^6)+2p_1xy+p_2(r^2+2x^2) \\ \\ y_{distorted}=y(1+k_1r^2+k_2r^4+k_3r^6)+2p_2xy+p_1(r^2+2y^2) \\ \tag{6} \end{cases}
⎩
⎨
⎧xdistorted=x(1+k1r2+k2r4+k3r6)+2p1xy+p2(r2+2x2)ydistorted=y(1+k1r2+k2r4+k3r6)+2p2xy+p1(r2+2y2)(6)
- 其中, r 2 = x 2 + y 2 r^2=x^2+y^2 r2=x2+y2( r r r是图像上某一点离图像中心点的距离), k i k_i ki和 p i p_i pi都是系数。
- x , y x,y x,y是输入的原始像素坐标点, x d i s t o r t e d , y d i s t o r t e d x_{distorted},y_{distorted} xdistorted,ydistorted是 x , y x,y x,y产生畸变后的坐标点。
- 另外,多项式 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 1+k_1r^2+k_2r^4+k_3r^6 1+k1r2+k2r4+k3r6的原始公式其实是 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 + k 4 r 8 + k 5 r 1 6.... 1+k_1r^2+k_2r^4+k_3r^6+k_4r^8+k_5r^16.... 1+k1r2+k2r4+k3r6+k4r8+k5r16....,但经一些学者论证,增加系数,对最终计算出的结果影响不大,甚至随着系数的增加效果会变差;因此在相机标定中,我们常见的畸变系数 k k k只有 k 1 , k 2 k_1,k_2 k1,k2,最多到 k 3 k_3 k3就结束了,因为大家默认 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 1+k_1r^2+k_2r^4+k_3r^6 1+k1r2+k2r4+k3r6 这个多项式已经足够去表示畸变模型,没必要再去增加其他系数了。

思考:当 k > 0 时,是桶型畸变还是枕型畸变?
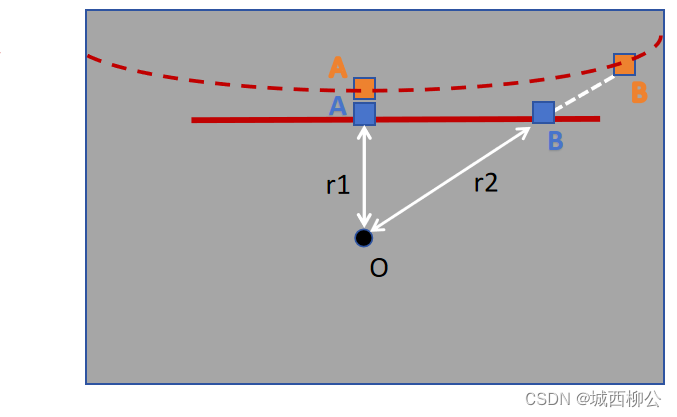
如图6, O O O是图像的中心点, A , B A,B A,B是在 X X X方向上的两个点, r 1 , r 2 r_1,r_2 r1,r2 分别是点 A , B A,B A,B离图像中心点 O O O的距离值,在 k > 0 k>0 k>0的情况下,根据上述畸变模型多项式得到 x , y x,y x,y方向上的畸变偏移值( x d i s t o r t e d x_{distorted} xdistorted, y d i s t o r t e d y_{distorted} ydistorted)都是大于0的,且偏移值的大小与 r r r成正比,即 r r r值越大,畸变偏移值越大;所以离中心点越近的点,畸变值小;离中心点越远的点,畸变值越大;因此最终会形成枕型畸变(红色实线代表畸变前,红色虚线代表畸变后)。
经过4个坐标系之间的转换,我们得到真实世界坐标下的一个3维点 ( X , Y , Z ) (X,Y,Z) (X,Y,Z)映射到像素坐标系下的坐标是 ( u , v ) (u,v) (u,v),再经过畸变模型处理,得到最终的畸变图像,这也是相机拍摄产生图像畸变的过程(三次矩阵连乘+畸变多项式)。我们知道,相机标定的主要目的是需要将相机拍摄的畸变图像还原到畸变之前,而这个 还原的过程 是与 相机成像的过程 是相反的,并且还原所需要的参数就是3个坐标系转换矩阵的参数和畸变系数。
而如何获取 3 个坐标系转换矩阵的参数和畸变系数(即内参和外参)的过程就是相机标定的过程。 \bf\color {red} {而如何获取3个坐标系转换矩阵的参数和畸变系数(即内参和外参)的过程就是相机标定的过程。} 而如何获取3个坐标系转换矩阵的参数和畸变系数(即内参和外参)的过程就是相机标定的过程。
1.4 内参&外参
相机标定具体要标定什么?
标定的是3个坐标转换矩阵中所涉及的参数
内参: f x f_x fx, f y f_y fy, c x c_x cx, c y c_y cy, k 1 k_1 k1, k 2 k_2 k2, k 3 k_3 k3, p 1 p_1 p1, p 2 p_2 p2
外参: R R R, t t t
- f x f_x fx, f y f_y fy是相机物理成像平面,在 X , Y X,Y X,Y方向上,每毫米分别对应的像素数量;
- c x c_x cx, c x c_x cx是图像坐标系原点在像素坐标系下的坐标;
- k 1 k_1 k1, k 2 k_2 k2, k 3 k_3 k3, p 1 p_1 p1, p 2 p_2 p2是畸变参数;
- R R R, t t t 分别是刚体变换的旋转矩阵和平移矩阵。
- 在相机标定中,针对同一相机,它的内参是固定的;外参则是由相机拍摄时的位姿决定的,也就是说,每拍摄一张图片,就会有一组外参。
可以看出:
内参:图像坐标系到像素坐标系的转换矩阵参数(这个转换过程是2维到2维的转换)+ 畸变参数;
外参:世界坐标系到相机坐标系的转换矩阵参数(这个转换过程是3维到3维的转换)。
1.4.1 目标函数
那如何得到内参和外参呢?我们需要建立一个目标函数:
∑
i
=
1
n
∑
j
=
1
m
∥
m
i
j
−
m
^
(
A
,
R
i
,
t
i
,
M
j
)
∥
2
(7)
\sum \limits_{i=1}^n\sum \limits_{j=1}^m\begin{Vmatrix} m_{ij}-\hat{m}(A,R_i,t_i,M_j) \\ \end{Vmatrix} ^2 \tag{7}
i=1∑nj=1∑m
mij−m^(A,Ri,ti,Mj)
2(7)
加入畸变的目标函数如下:
∑
i
=
1
n
∑
j
=
1
m
∥
m
i
j
−
m
^
(
A
,
k
1
,
k
2
,
R
i
,
t
i
,
M
j
)
∥
2
(8)
\sum \limits_{i=1}^n\sum \limits_{j=1}^m\begin{Vmatrix} m_{ij}-\hat{m}(A, k_1,k_2,R_i,t_i,M_j) \\ \end{Vmatrix} ^2 \tag{8}
i=1∑nj=1∑m
mij−m^(A,k1,k2,Ri,ti,Mj)
2(8)
其中,
- n n n 是标定使用的图片张数, m m m 是每张图片上选取的角点数;
- m i j m_{ij} mij 是相机拍摄的 第 i i i 图像中所提取出的角点数据, m ^ \hat{m} m^ 是根据坐标转换关系计算出来的与 m i j m_{ij} mij角点 对应的像素值。
- 对所有标定图片上的角点对进行差平方求和。
- 优化该目标函数,使得目标函数的值最小。
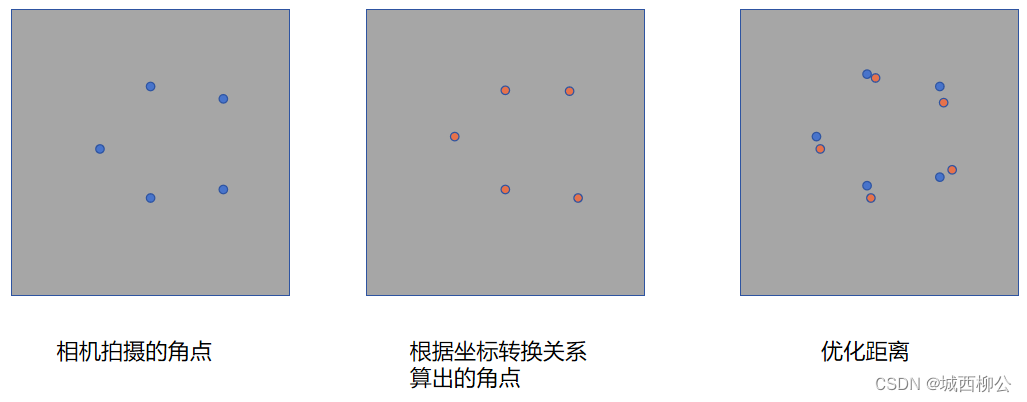
- 图7左图中的蓝色点为相机拍摄的真实图像,经角点提取算法处理后的角点;
- 图7中间图中的红色点为经过3次坐标转换和畸变多项式计算出的与绿色角点一 一匹配的角点;
- 图7右图为蓝色角点与红色角点之间的误差距离。
所以我们需要优化目标函数,使得真实图像上的角点与计算出的角点,它们之间的误差距离越小越好。(图6右图, 偏移的产生一般是由相机硬件的精度不足产生的)。
那为什么现在的标定方法没有直接用这种最优化的方法,而是使用张正友标定法?
- 这是因为目标函数要优化的参数太多了。
- 当我们在第一次进行标定的时候,所有的内参和外参我们是不知道的,所以要凭经验给定一个初始值,如果初始值不好的话,后续在对初始化后的内参、外参的值进行更新/优化时,很容易陷入局部最优解,甚至根本无法得到最优解。接下来,我们具体来看看标定时需要优化的参数有哪些?
假如在没有任何先验知识的情况下,拍摄了20张图片进行标定,我们来看看具体需要求解多少个参数。
- 内参: f x f_x fx, f y f_y fy, c x c_x cx, c y c_y cy, k 1 k_1 k1, k 2 k_2 k2, k 3 k_3 k3, p 1 p_1 p1, p 2 p_2 p2,共9个;
- 外参:每一张图片都有一组 R R R, t t t;而每一个 R R R 有9个未知量, t t t 有3个未知量,共(9+3)* 20 = 720个。
所以需要优化的内外参共有:729个;而且每增加一张图片, R R R, t t t 的未知量个数还会增加,所以使用这种先随机初始化参数,再去慢慢优化目标函数的方式,是无法求解出最优解的。
因此提出了张正友标定法,它是通过数值解法,解出了一个比较准确的内外参初始值;在进行目标函数初始化参数的时候能给到一个好的初始值,最终使得在目标函数优化结束后,能得到一个比较准确的标定结果。所以,我们要明确张正友方法的贡献到底是什么,它不是提出了一个新的目标函数,而是它通过相机成像原理等一系列先验条件,求解出了一个非常好的数值解,这个数值解最终被用在了目标函数的优化当中。
2、张正友标定法
本文主要是以应用为主,所以张正友方法所涉及的详细公式的推导,在这里就不做详细的讲解了,感兴趣的同学可以自行查看官方文档,接下来主要介绍下张正友方法中的一些关键点,方便大家理解。
2.1 标定平面
- 在世界坐标系下的标定平面,必须处于
Z
w
=
0
Z_w=0
Zw=0 的一个平面上(即标定板上的点必须处于
Z
w
=
0
Z_w=0
Zw=0 的平面上);
图8. 标定平面示意图
在实际的标定场景中,我们经常会看到有人拿一块泡沫塑料板,并在上面粘一个棋盘格打印纸去做标定,如果泡沫塑料板是凹凸不平的话,这样就在一开始就引入误差了;如果使用张正友标定方法的话,就必须把这个标定平面给做平了。
2.2 求解内外参
2.2.1 求解单应性矩阵
单应性矩阵:表示的是一个平面与另一个平面的映射关系。
s
[
u
v
1
]
=
A
[
r
1
r
2
r
3
t
]
[
X
Y
0
1
]
(9)
s\begin{bmatrix} u \\ v \\ 1 \end{bmatrix}= A \begin{bmatrix} r_1& r_2 & r_3 & t\end{bmatrix}\begin{bmatrix} X \\ Y \\ 0 \\ 1 \end{bmatrix} \tag{9}
s
uv1
=A[r1r2r3t]
XY01
(9)
因为张正友方法规定了标定板处于
Z
w
=
0
Z_w=0
Zw=0 平面 ,所以
r
3
r_3
r3 不起作用,可将公式(9)简化到公式(10),方便后续计算:
s
[
u
v
1
]
=
A
[
r
1
r
2
t
]
[
X
Y
1
]
(10)
s\begin{bmatrix} u \\ v \\ 1 \end{bmatrix}= A \begin{bmatrix} r_1& r_2 & t\end{bmatrix}\begin{bmatrix} X \\ Y \\ 1 \end{bmatrix} \tag{10}
s
uv1
=A[r1r2t]
XY1
(10)
其中,
H
=
A
[
r
1
r
2
t
]
(11)
H= A \begin{bmatrix} r_1& r_2 & t\end{bmatrix} \tag{11}
H=A[r1r2t](11)
- 单应性矩阵, A A A是相机所有内参的矩阵, [ r 1 r 2 t ] \begin{bmatrix} r_1& r_2 & t\end{bmatrix} [r1r2t] 是外参矩阵;
- 假如有两个平面,每个平面上各有一些角点,并且这些角点都是一 一对应的关系,如图7,那么这个一 一对应的关系,我们可以用一个矩阵表示,这个矩阵称之为单应性矩阵;
因此,如果我们知道了两个平面上角点的对应关系,就可以求出对应的单应性矩阵 H H H 。而在实际的标定过程中,真实拍摄图片上的角点和根据相机成像模型计算出的角点(如图7的左边两个图)的一 一对应关系是可以获取的,根据这些对应关系,将数值代入公式(10)中,即可求得单应性矩阵 A A A,具体数学求解步骤就不详细讲解。
2.2.2 根据单应性矩阵 H H H求解内外参(即标定时目标函数的内外参初始值)
根据2.2.1的内容求解出单应性矩阵 H H H之后,由于 H H H是内参矩阵和外参矩阵的混合体,而我们的目的是分别得到内参和外参,所以需要先求出内参(因为内参比外参更容易求出,这是因为每张标定图片的内参都是固定不变的,而外参因为不同的标定图片是不同的),得到内参后,再外参即可求出。
1、求解内外参是张正友方法的主要工作,具体步骤如下:
使用
[
h
1
h
2
h
3
]
\begin{bmatrix} h_1& h_2 & h_3\end{bmatrix}
[h1h2h3]表示单应性矩阵
H
H
H,则有
[
h
1
h
2
h
3
]
=
λ
A
[
r
1
r
2
t
]
(12)
\begin{bmatrix} h_1& h_2 & h_3\end{bmatrix}= \lambda A \begin{bmatrix} r_1& r_2 & t\end{bmatrix} \tag{12}
[h1h2h3]=λA[r1r2t](12)
- [ r 1 r 2 t ] \begin{bmatrix} r_1& r_2 & t\end{bmatrix} [r1r2t] 是刚体变换,也就是公式(1),而公式(1)中的 R R R是一个3*3的旋转矩阵,我们知道旋转矩阵又是正交矩阵(即行列向量两两正交,且向量模长为1);所以在 [ r 1 r 2 t ] \begin{bmatrix} r_1& r_2 & t\end{bmatrix} [r1r2t] 中, r 1 r_1 r1 垂直于 r 2 r_2 r2 , r 1 r_1 r1 的模长等于 r 2 r_2 r2 的模长;
- 所以 r 1 ⋅ r 2 r_1 \cdot r_2 r1⋅r2= 0; r 1 ⋅ r 1 r_1 \cdot r_1 r1⋅r1= r 2 ⋅ r 2 r_2 \cdot r_2 r2⋅r2
公式(12)等式两边左乘
A
−
1
A^{-1}
A−1 得到:
A
−
1
[
h
1
h
2
h
3
]
=
λ
A
[
r
1
r
2
t
]
(13)
A^{-1} \begin{bmatrix} h_1& h_2 & h_3\end{bmatrix}= \lambda A \begin{bmatrix} r_1& r_2 & t\end{bmatrix} \tag{13}
A−1[h1h2h3]=λA[r1r2t](13)
即:
h
1
T
A
−
T
A
−
1
h
2
=
0
(14)
h_1^{T}A^{-T}A^{-1} h_2=0 \tag{14}
h1TA−TA−1h2=0(14)
h
1
T
A
−
T
A
−
1
h
1
=
h
2
T
A
−
T
A
−
1
h
2
(15)
h_1^{T}A^{-T}A^{-1} h_1=h_2^{T}A^{-T}A^{-1} h_2 \tag{15}
h1TA−TA−1h1=h2TA−TA−1h2(15)
- 公式(14)即为: r 1 ⋅ r 2 r_1 \cdot r_2 r1⋅r2= 0 ;
- 公式(15)即为: r 1 ⋅ r 1 r_1 \cdot r_1 r1⋅r1= r 2 ⋅ r 2 r_2 \cdot r_2 r2⋅r2
- 这样就可把外参剥离出去,只求内参;
接下来就是各种公式的计算了:
令:

-
B
B
B 是对称矩阵,因此9个元素中只需要确定6个元素即可,即公式(17)。
b = [ B 11 , B 12 , B 22 , B 13 , B 23 , B 33 ] (17) b= \begin{bmatrix} B_{11},B_{12} ,B_{22},B_{13}, B_{23}, B_{33}\end{bmatrix} \tag{17} b=[B11,B12,B22,B13,B23,B33](17) - 由公式(16)可以看出,
b
b
b 中的每个元素又是由相机内参确定的,即
b
b
b 是由相机内参的未知量组合而成。
v i j = [ h i 1 h j 1 , h i 1 h j 2 + h i 2 h j 1 , h i 2 h j 2 , h i 3 h j 1 + h i 1 h j 3 , h i 3 h j 2 + h i 2 h j 3 , h i 3 h j 3 ] T (18) v_{ij}= \begin{bmatrix} h_{i1}h_{j1},h_{i1}h_{j2} + h_{i2}h_{j1},h_{i2}h_{j2}, h_{i3}h_{j1}+h_{i1}h_{j3}, h_{i3}h_{j2} + h_{i2}h_{j3}, h_{i3}h_{j3}\end{bmatrix}^{T} \tag{18} vij=[hi1hj1,hi1hj2+hi2hj1,hi2hj2,hi3hj1+hi1hj3,hi3hj2+hi2hj3,hi3hj3]T(18) - v i j v_{ij} vij 由单应性矩阵组成,因为 H H H 已知,所以 v i j v_{ij} vij 也是已知的。
- v i j v_{ij} vij 的维度是6。
接下来需要解方程:
[
v
12
T
(
v
11
−
v
22
)
T
]
b
=
0
(19)
\begin{bmatrix} v_{12}^{T} \\ (v_{11} - v_{22})^{T}\end{bmatrix} b= 0 \tag{19}
[v12T(v11−v22)T]b=0(19)
简化后为:
V
⋅
b
=
0
(20)
V \cdot b= 0 \tag{20}
V⋅b=0(20)
- 对于一张照片,就会有一个 V b = 0 Vb= 0 Vb=0 的方程,这是一个 2维 ⋅ \cdot ⋅ 6维 = 0 的方程;
- 而一张照片是无法唯一确定方程中的 b b b 。
至少需要几张照片才能唯一确定 b ?
对于一个相机,它的内参是不变的,而它的外参则是每一张标定图片对应一组外参;因此至少需要3张图片,才能唯一确定参数 b b b ;标定时使用的照片数量越多的话,公式(19)就变成了一个冗余方程,这样的方程抗噪声能力就越强,所以在实际标定时不会仅仅采集3张图片就去做标定。
- 对于一个冗余方程 V b = 0 Vb= 0 Vb=0 , V T ⋅ V V^T \cdot V VT⋅V (矩阵),它(矩阵)的最小特征值的特征向量就是 b b b 的解。
到目前为止,根据张正友的方法,我们通过解冗余方程的方式已经将
b
b
b (内参未知量)求解出来了。
若想获取外参,可将求解出的内参未知量代入公式(11)中,即可求出对应的外参。
张正友方法解出的内外参是代数意义上的最优解(是目标函数优化时的初始值),而目标函 \bf\color {red} {张正友方法解出的内外参是代数意义上的最优解(是目标函数优化时的初始值),而目标函} 张正友方法解出的内外参是代数意义上的最优解(是目标函数优化时的初始值),而目标函
数解出的内外参才是物理意义上的最优解(是标定的最终结果)。 \bf\color {red} {数解出的内外参才是物理意义上的最优解(是标定的最终结果)。} 数解出的内外参才是物理意义上的最优解(是标定的最终结果)。
2.3 目标函数优化
目标函数:
∑
i
=
1
n
∑
j
=
1
m
∥
m
i
j
−
m
^
(
A
,
R
i
,
t
i
,
M
j
)
∥
2
\sum \limits_{i=1}^n\sum \limits_{j=1}^m\begin{Vmatrix} m_{ij}-\hat{m}(A,R_i,t_i,M_j) \\ \end{Vmatrix} ^2
i=1∑nj=1∑m
mij−m^(A,Ri,ti,Mj)
2
上述张正友方法得到的只是一个较好的初始值,需要代入目标函数,对内外参进行迭代更新,最终优化迭代得到的内外参才是物理意义上的最优解。迭代的方法是:将3维点依次投影到2维图像上,然后和相机拍摄的图像上的2维角点,进行求差,这个差值是一个具有物理含义的值,我们将这个差值进行最优化。
加入畸变的目标函数:
∑
i
=
1
n
∑
j
=
1
m
∥
m
i
j
−
m
^
(
A
,
k
1
,
k
2
,
R
i
,
t
i
,
M
j
)
∥
2
\sum \limits_{i=1}^n\sum \limits_{j=1}^m\begin{Vmatrix} m_{ij}-\hat{m}(A, k_1,k_2,R_i,t_i,M_j) \\ \end{Vmatrix} ^2
i=1∑nj=1∑m
mij−m^(A,k1,k2,Ri,ti,Mj)
2
与上面的标准目标函数的迭代方法不同,加入畸变的目标函数迭代方法,不是直接将3维点投影到2维图像上,而是在投影到2维图像之前,需要引入畸变,变成一个新的点,然后再和相机拍摄的图像上的2维角点,进行求差,最后对这个差值就行最优化。
由于张正友方法是在2000年提出的,时间比较久远,到目前为止,很多人都对该方法作了一些改进。
3、改进方法
3.1 使用圆环或棋盘格进行标定
- 对于张正友标定法,它只是提供了内外参的获取方法,并没有对使用何种标定图案进行限制。
- 为提高标定效果,现在大多使用棋盘格或者圆环的图案进行标定。
3.2 圆环与棋盘格的优缺点分别是什么?
有论文验证,在标定时,使用圆环进行标定,其标定的精度和鲁棒性要高于棋盘格。只有在标定时,了解圆环和棋盘格各自的优缺点,才能根据实际的标定情况选择合适的标定方式;
- 圆检测精度高,主要表现为中心点拟合精度高,但是具有偏心误差;
- 棋盘格检测精度低,但不存在偏心误差;
3.2.1 什么是偏心误差
- 对于棋盘格而言,我们要使用的角点其实就是两条直线的交点。
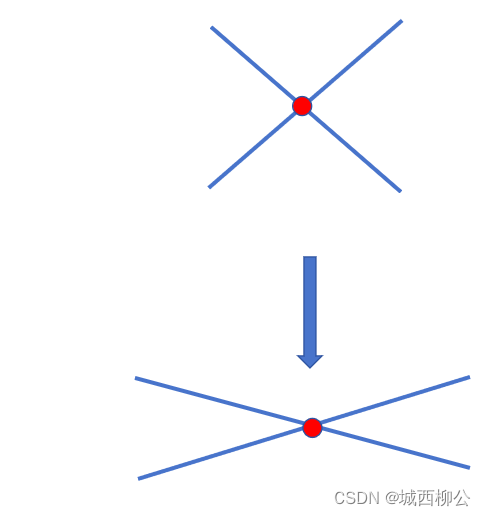
图9. 直线投影示意图
从相机角度看,两条直线可能存在变形,但是两条直线的交点依旧代表现实中的交点在相机中的位置,即投影交点与相机实际成像交点重合,如图9所示(上面的两条直线为3维世界中的两条直线,下面的两条直线为相机拍摄的画面)。
- 对于圆环而言,我们要使用的角点其实是圆心。
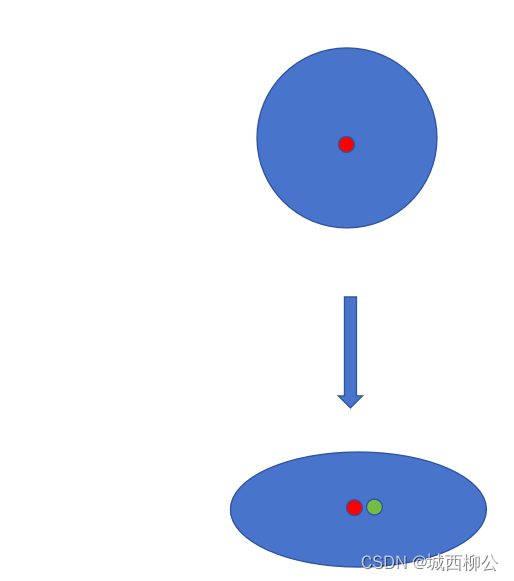
图10. 圆投影示意图
从相机角度看,只要不是在圆的正上方拍摄,圆在相机上的投影一定是椭圆,但对于实际相机拍摄的图像,椭圆的中心与投影中心不重合,存在偏差,即为偏心误差,如图10所示(上面的圆心为3维世界中的圆心,下面的圆心为投影圆心和实际相机拍摄的圆心);也就是说,圆的中心的投影不等于投影椭圆的中心。
由于偏心误差的存在,所以在使用圆环进行标定的时候,一开始就引入了误差,因此在标定时大多数人会选取棋盘格进行标定。
如何去解决偏心误差的问题呢?
目前最好的方法是这个论文 << Accurate camera calibration using iterative refinement of control points>> 所提出的方法,也是使用圆环标定用的最多的优化方法,其大致思路是:
- 3维世界中的圆投影出的椭圆,根据投影关系,将这个椭圆投影回正圆,检测正圆的圆心,再将圆心投影回去,即为椭圆的圆心;这样就解决了偏心误差对标定结果的影响。
- 这个方法比棋盘格的标定效果好很多。具体实现方法和代码可看论文。
- 如果直接使用圆环进行标定,不解决偏心误差的问题,那么标定出的效果可能和棋盘格的效果一样,甚至会更差;所以使用圆环进行标定时,需要解决偏心误差。





















 2503
2503











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








