三维空间中的两直线相交

        很多资料上提供的两直线相交求点问题一般都是基于二维空间的，而且是直接使用坐标系进行求解。实际上知道二维空间中的求法（使用坐标系进行求解的），要想从中推导到三维空间中的求法是不容易的。在进行几何问题求解时，除了使用坐标系求解问题外，使用向量求解问题也许更容易。向量空间是隐藏坐标系的，使用向量空间求解几何问题比使用坐标系求解问题更好的是，它将问题的解法提升到了一个宏观的高度，并且有了基于向量空间的解法，那么可以把这个解法直接延伸到n维都很容易。

        假设有两直线l1和l2，它们的参数方程如下所示：(向量v1,v2均为单位向量)

l1: P1 = R1 + t1v1;
l2: P2 = R2 + t2v2.

两直线平行、异面和相交的判断方法：

平行：v1×v2 = 0；

异面：(R2-R1, v1, v2) ≠ 0；

相交：(R2-R1, v1, v2) ＝ 0且v1×v2 ≠ 0。

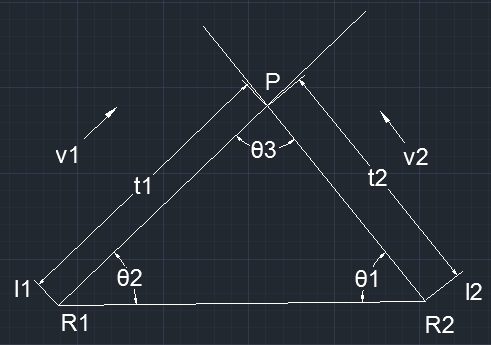
若相交，那么需要求出两直线的交点。如下图所示：

两直线交点为P，|R1P| = t1，|R2P| = t2。根据三角形正弦定理，△R1R2P中，t1/sinθ1 = t2/sinθ2 = |R1R2|/sinθ3，要求交点，可先求得t1或t2，t1,t2的值可通过正弦定理求得。两向量夹角的正弦值是隐藏在向量外积的长度上的，如上图所示，θ3是向量v1,v2的夹角，则|v1×v2| = sinθ3。

        可立方程：(R1-R2)×v2 = t1(v2×v1)，因为|(R1-R2)×v2| = |R1R2|sinθ1。可求得：t1 = (R1-R2)×v2/(v2×v1)，同理，可求得t2 = (R2-R1)×v1/(v1×v2)，将t1代入l1方程即可得到交点P，或将t2代入l2方程也可得到交点P，两者只需求其一。

        但是在计算机中，由于同一直线，它的参数方程可有多种描述（起点可选不同的点，或者单位方向向量可不同），参数t可为正值也可为负值。所以需要将对两直线相交的情况分为四种，上述是第一种情况，第二种是只需对l1做反向延长线进行求交，第三种是只需对l2做反向延长线进行求交，第四种是需要对l1和l2均做反向延长线进行求交。

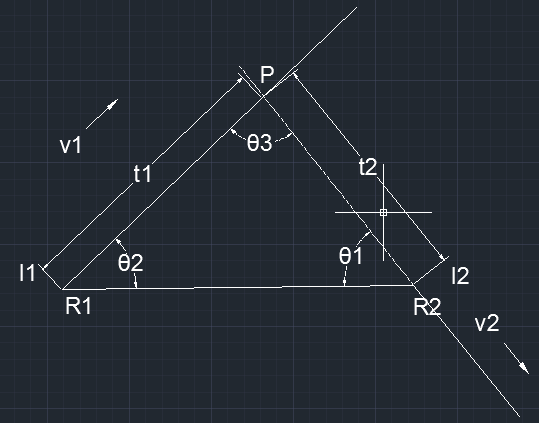
        第二种情况和第三种情况可视为同一种情况，这里只对第三种情况进行分析。第三种情况如下图所示：

则相对第一种情况，在这种情况下，t1' = t1 = (R1-R2)×v2/(v2×v1), t2' = t2 = (R2-R1)×v1/(v1×v2)，只不过t1‘的值为正值，t2’的值为负值。

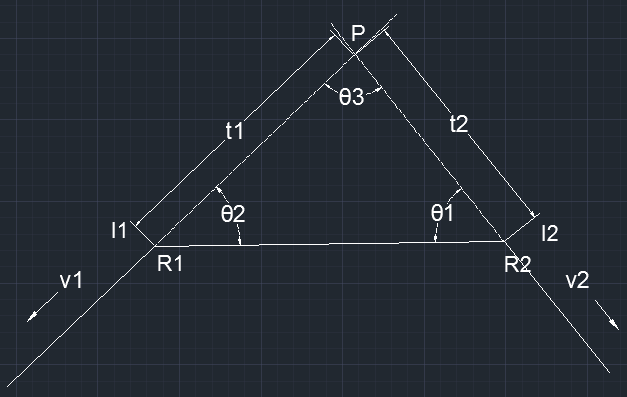
        第三种情况如下图所示：

则相对第一种情况，在这种情况下，t1'‘ = t1 = (R1-R2)×v2/(v2×v1), t2'’ = t2 = (R2-R1)×v1/(v1×v2)，只不过t1''和t2''的值均为负值。

        综上四种情况，t1和t2的求解公式都是一样的，即t1 = (R1-R2)×v2/(v2×v1)，t2 = (R2-R1)×v1/(v1×v2)。