Numpy系列（八）：函数库之5傅里叶变换函数

Numpy系列目录

---

一、 简介

傅里叶变换是将时域数据转换成频域数据。傅里叶反变换可以从频域还原数据。

计算机处理的数据通常是离散数据，因此数值计算中的傅里叶变换都是离散傅里叶变换。
Numpy中提供了基于快速傅里叶变换（FFT）方法实现的离散傅里叶变换（DFT）常用函数，
同时还提供了用于计算频域频率的工具函数。

二、 思维导图

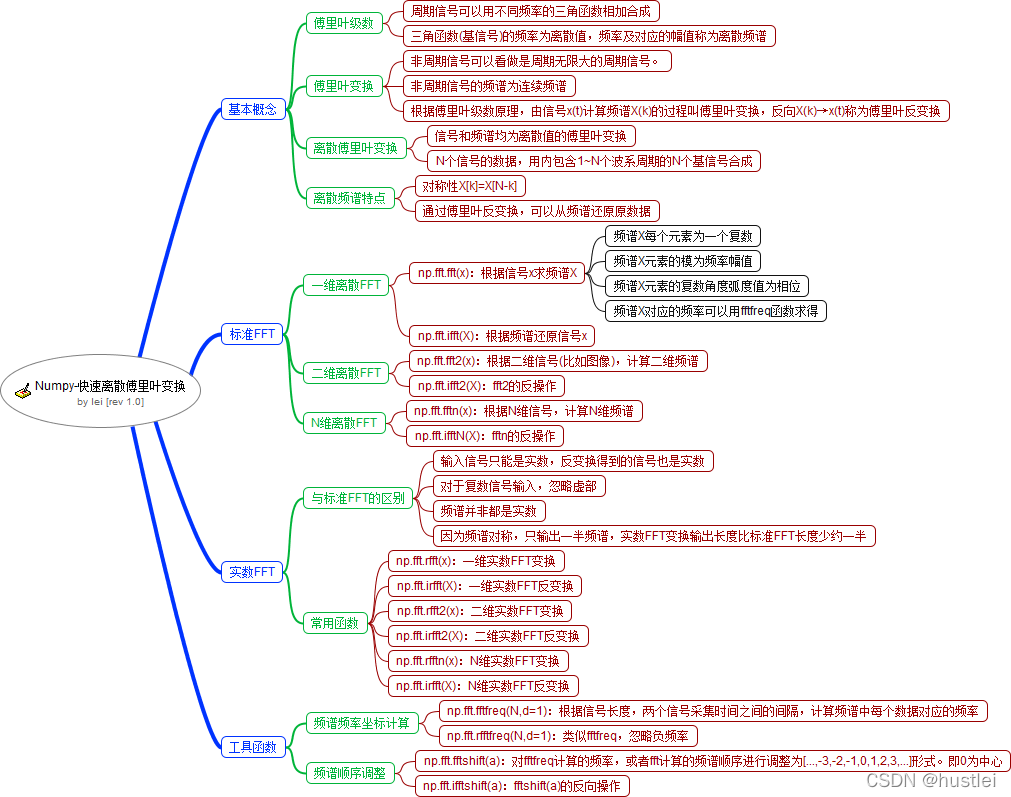
三、 傅里叶变换基础知识

1. 傅里叶级数

傅里叶级数：任意周期函数(信号)可用多个周期函数（基函数，通常为三角函数）相加而合成。即傅里叶级数就是把一个周期函数表示成三角函数的级数。

周期信号$x(t)$，周期为$T_0$，频率$f_0=1/T_0$，角频率为${\omega }_0=\frac{2\pi }{T_0}$。其傅里叶级数展开为：

$$x(t)=\frac{a_0}{2}+\sum _{n=1}^{\infty }[a_n\cos (n{\omega }_{0}t)+b_n\sin (n{\omega }_{0}t)]$$

$$x(t)=\frac{a_0}{2}+\sum _{n=1}^{\infty }{A}_n\sin (n{\omega }_{0}t+{\varphi }_n)=\frac{a_0}{2}+\sum _{n=1}^{\infty }{A}_n\cos (n{\omega }_{0}t+{\varphi }_n-\frac{\pi }{2})$$

以上两式等价。

式中：$a_n,b_n$称为傅里叶系数；$A_n=\sqrt{a_n^2+b_n^2}$为幅值，${\varphi }_n=\arctan \frac{b_n}{a_n}$(弧度)为相位。

$$\begin{gathered} a_n=\frac{2}{T_0}{\int }_{\frac{-T_0}{2}}^{\frac{T_0}{2}}x(t)\cdot \cos (n{\omega }_{0}t)dt \\ {b}_n=\frac{2}{T_0}{\int }_{\frac{-T_0}{2}}^{\frac{T_0}{2}}x(t)\cdot \sin (n{\omega }_{0}t)dt \end{gathered}$$

2. 复数形式傅里叶级数

$$x(t)=\sum _{n=-\infty }^{\infty }{c}_n{e}^{\text{j}n{\omega }_{0}t}$$

式中：${\omega }_0=\frac{2\pi }{T_0}，\text{j}=\sqrt{-1}，c_n也称作离散频谱$。

$$c_n=\frac{1}{T_0}{\int }_{\frac{-T_0}{2}}^{\frac{T_0}{2}}x(t)e^{-\text{j}n{\omega }_{0}t}dt$$

3. 傅里叶变换

周期函数(信号)可以用傅里叶级数来表达，傅里叶系数又叫做离散频谱。称为离散频谱，是因为谱线只出现在频率$f_0=1/T_0，{\omega }_0=2\pi /T_0$的整数倍上。

对于周期信号：

$$x(t)=\sum _{n=-\infty }^{\infty }X(n{\omega }_0)e^{\text{j}n{\omega }_{0}t}$$

$$X(n{\omega }_0)=\frac{1}{T_0}{\int }_{\frac{-T_0}{2}}^{\frac{T_0}{2}}x(t)e^{-\text{j}n{\omega }_{0}t}dt$$

对于非周期信号$x(t)$，可以认为是周期无限大。即$T_0\to \infty$，则${\omega }_0=2\pi /T_0\to 0$。用$\omega =n{\omega }_0$，则$\omega$变成了连续变量，离散频谱变成了连续频谱。

$$X(\omega )={\int }_{-\infty }^{\infty }x(t)e^{-\text{j}\omega t}dt$$

把连续频谱带入傅里叶级数，可以得到：

$$x(t)=\frac{1}{2\pi }{\int }_{-\infty }^{\infty }X(\omega )e^{\text{j}\omega t}d\omega$$

根据频谱计算信号，即：$X(\omega )\to x(t)$，也称为逆傅里叶变换，或傅里叶反转换。

4. 离散傅里叶变换

连续信号的傅里叶变换的作用主要是理论价值，但实际应用的都是离散傅里叶变换。

离散傅里叶变换（DFT）是指傅里叶变换在时域和频域上都呈现离散的形式。
将时域信号的采样，变换为在离散时间傅里叶变换（DTFT）频域的采样。

离散傅里叶级数

对时间上连续的信号进行采样，可以把信号离散化。对于采样序列：

$$[x_0,x_1,\dots ,x_n,\dots ]$$

$x[n]$表示第n个采样信号。

对于离散信号，傅里叶变换也就是傅里叶级数。如果信号$x[n]$周期为N，则$x[n]=x[n+N]$。按照傅里叶级数的思路，它可以表达为角频率为"${\omega }_0=2\pi /N$的整数倍"的三角函数的和。

周期为N的无限长度周期信号，和长度为N的信号是等价的。可以用长度为N的信号序列表示：$[x_0,x_1,\dots ,x_n,\dots ,x_N]$

取k作为频率倍数参数，即$\omega =k{\omega }_0=2\pi k/N$，则傅里叶变换为：

$$x[n]=\sum _{k=0}^{N-1}X[k]e^{\text{j}\frac{2\pi k}{N}n}$$

$$X[k]=\frac{1}{N}\sum _{n=0}^{N-1}x[n]e^{-\text{i}\frac{2\pi k}{N}n}$$

• 离散傅里叶变换：$x[n]\to X[k]$
• 逆离散傅里叶变换：$X[k]\to x[n]$

$x[n]$表示第n个采样信号，$X[k]$表示角角频率为$\omega =\frac{2\pi k}{N}$的频谱。

离散傅里叶变换进一步说明

1）三角函数的特点

• t在[0-1]范围内波形具有一个周期（圆频率$\omega =2\pi$）

$$\begin{array}{r}\cos (\omega t)=\cos (2\pi t)\\ \sin (\omega t)=\sin (2\pi t)\end{array}$$

• t在[0-N]范围内波形具有一个周期（圆频率$\omega =2\pi /N$）

$$\cos (\omega t)=\cos (\frac{2\pi }{N}t)$$

• t在[0-1]范围内波形内具有k个周期（圆频率$\omega =2\pi k$）

$$\cos (\omega t)=\cos (2\pi kt)$$

• t在[0-N]范围内波形具有n个周期（圆频率$\omega =\frac{2\pi k}{N}$）

$$\cos (\omega t)=\cos (\frac{2\pi k}{N}t)$$

$\omega =0$则波形为常量，即直线。

2） 离散信号

在[0-T]时间段采样N次（采样频率为$f_s=N/T$），得到信号序列x：

$$[x_0,x_1,\dots ,x_n,\dots ,x_N]$$

$x[n]$表示第n个采样，即信号在时间$t=\frac{n}{N}T$处的信号幅值。

根据离散傅里叶变换，$x[n]$可以表示为角频率$\omega =\frac{2\pi k}{N}$的三角函数的线性和。每个频率的三角函数称为一个基信号。

3）基信号

对于样本数为N的信号采样。离散基信号最多为N个，即：

$$e^{\text{i}\frac{2\pi k}{N}t}=\cos (\frac{2\pi k}{N}t)+\text{i}\sin (\frac{2\pi k}{N}t),k=0...N-1$$

k=N与k=0相同，均恒为1，可以表示常量。

因此，任意离散信号序列，都可以用离散傅里叶级数表示（直接用n表示时间维度变量）：

$$x[n]=\sum _{k=0}^{N-1}X[k]e^{\text{j}{\omega }_{k}n}=\sum _{k=0}^{N-1}X[k]e^{\text{j}\frac{2\pi k}{N}n}$$

频谱$X[k]$：

$$X[k]=\frac{1}{N}\sum _{n=0}^{N-1}x[n]e^{-\text{i}{\omega }_{k}n}=\frac{1}{N}\sum _{n=0}^{N-1}x[n]e^{-\text{i}\frac{2\pi k}{N}n}$$

• 频谱$X[k]$具有对称性，即$X[k]=X[N-k]$。所以我们一般只看前一半数据就ok了。

• 频谱通过傅里叶级数（离散傅里叶反/逆变换）可以重新得到原信号

频谱$X[k]$为复数，与原信号的关系：

• X[k]的模为对应基信号分量幅值

• X[k]的复数角度（弧度）为对应基信号的相位

FFT之后某个频率分量为复数$a_n+b_{n}j$表示，那么这个复数的模就是$A_n=\frac{\sqrt{a_n^2+b_n^2}}{N}$，相位就是${\varphi }_n=\arctan (\frac{b_n}{a_n})$。

注意：因为对称型，第n个频率和第N-n个频率实际上是一个值，因此，我们在只看一半数据时，可以认为$A_n=2\frac{\sqrt{a_n^2+b_n^2}}{N}$，

四、 Numpy快速傅里叶变换

1. 标准FFT

在实际应用中通常采用快速傅里叶变换(FFT)以高效计算DFT。

计算n个数值组成的一维数据的离散傅里叶变换(DFT)，使用快速傅里叶变换算法CT。

1.1 一维离散FFT

• freq=np.fft.fft(x)
  • x：输入数据，可以是复数。
  • X：输出频谱。
    • X[i]:表示角频率$\omega =\frac{2\pi i}{N}$（采样范围内有i个周期）的频谱幅值。
      • X[i]与X[n-i]共轭，幅值相等。只看前一半数据就ok了。
      • X[0]表示常数项，其实部等于输入数据实部的和。

示例：对于$x(t)=\cos (2\pi t+0.5)+3\sin (2\pi 3t)$。

其频域$X[k]$：

• X[0]为常数项

• X[1]幅值为1，相位为0.5

• X[3]幅值为3，相位为0

>>> t=np.linspace(0,2,200)                 #采样时长T=2
>>> x=np.cos(2*np.pi*t+0.5) + 3*np.cos(2*np.pi*3*t)  #采样数据
>>> X=np.fft.fft(x)                        #求频谱
>>> A=(X.real**2+X.imag**2)**0.5*2/200     #求幅值
>>> PHI=np.angle(X)                        #求相位
>>> A,PHI = np.round(A,2),np.round(PHI,2)  #四舍五入，方便观察
>>>
>>> #频率为1即角频率为2π的频谱，k=1，由于采样时长T=2,所以其序号为k=i/T即k=1对应i=2
>>> #原理见本例后说明。同样频率为3角频率为3×2π的频谱，k=3,序号i为6
>>> A[2],A[6],PHI[2],PHI[6]  #幅值和相位与公式基本一致，采样时长增加，会更加准确
(1.03, 3.0, 0.51, 0.09)

我们知道频谱$X[k]$中的$k$值实际上是基信号（三角函数）频率，即三角函数单位时间内的周期个数。而圆频率$\omega =2\pi k$表示三角函数单位时间内走过的角度。

在离散傅里叶公式中我们用离散数据的序号n代替了时间t。实际上$t=n/f_s,f_s$为采样频率，即单位时间内采样的数据个数。采样个数（离散数据个数）为N，总采样时间为$T$,那么$f_s=N/T$。

由于我们用原信号数据序号n代替了t，用频谱序号i代替了频率k，那么$e^{-j\frac{2\pi k}{N}n}$，转换为$e^{-j\omega t}$形式，则为$e^{-j\frac{2\pi i{f}_s}{N}\frac{n}{f_s}}=e^{-j2\pi \frac{i}{T}\frac{n}{f_s}}$。即离散傅里叶变换计算得到的频谱实际上是$i\sim X[i]$，其中$i$为序号。转换为$k\sim X[k]$形式$e^{-j2\pi kt}$，则$k=\frac{i}{T}，t=\frac{n}{f_s}$。

在本文4中的工具函数fftfreq就是把频谱X的序号i转换为频率k的。其基本原理就是用X的下标除以采样时长T。

由上例可知，频谱序号和采样时长有关，当采样时长为小数，比如1.5时，同一频率的频谱会被分解为2-3三个上。

1.2 一维离散FFT反变换

• x=np.fft.ifft(X):根据频谱X求原始信号x

>>> x1=np.fft.ifft(X)  #使用上节np.fft.fft(x)计算的频谱求逆变换
>>> np.allclose(x,x1)  #逆变换得到的值与原始信号x基本相同
True

1.3 二维离散FFT

二维FFT公式：

$$F(u,v)=\int \int f(x,y)e^{-j2\pi (ux+vy)}dxdy$$

二维傅里叶变换就是将图像与每个不同频率的不同方向的复平面波做内积（先点乘在求和）

也就是求基函数$e^{-j2\pi (ux+vy)}$上投影的过程。不同方向上基信号波形的叠加。

• X=np.fft.fft2(x)：x为二维数据，输出频谱X也是二维数据

>>> x=np.array([[1,2,3],[1,2,3]])
>>> X=np.fft.fft2(x)
>>> X
array([[12.+0.j        , -3.+1.73205081j, -3.-1.73205081j],
       [ 0.+0.j        ,  0.+0.j        ,  0.+0.j        ]])

1.4 二维离散FFT逆转换

• x=np.fft.ifft2(X)：np.fft.fft2的逆向操作

>>> x1=np.fft.ifft2(X)
>>> np.allclose(x,x1)
True

1.5 多维离散FFT

类似二维离散fft

• X=np.fft.fftn(x)：根据N维数据计算FFT变换频谱X
• x=np.fft.fftn(X)：N维FFT逆变换，np.fft.fftn的反向操作

2. 实数FFT

• X=np.fft.rfft(x)： 计算实数输入的一维离散傅立叶变换。

  • x为复数时忽略虚部。
  • 频域X为复数

• x=np.fft.irfft(X)： 计算n点DFT的逆变换。

  • X可以为复数，但是逆变换后的x为实数。

• np.fft.rfft2(a): 计算实数组的二维FFT。

• np.fft.irfft2(a): 计算实数组的二维逆FFT。

• np.fft.rfftn(a): 计算实输入的N维离散傅立叶变换。

• np.fft.irfftn(a): 计算实输入的N维FFT的逆。

3. 工具函数

3.1 频谱频率坐标计算函数fftfreq

在画频谱图的时候，要给出横坐标的数字频率，这里可以用fftfreq给出。

正如2.1中所说，频率$k=i/T$，即频率等于频谱序号(下标)除以采样时长。

• k = np.fft.fftfreq(N, d=1.0)：根据采样数据个数N，d采样周期（间隔），计算频谱频率序列k

  • 第一个参数N是FFT的点数，一般取FFT之后的数据的长度（size）

  • 第二个参数d是采样周期，其倒数就是采样频率$f_s$，即$d=1/f_s=T/N,T为采样时长$

  • 得到的结果为各个数字频率 $k[i]=\frac{i}{T}=\frac{i{f}_s}{N}=\frac{i}{dn}$，即序列[$\frac{0}{dn},\frac{1}{dn}...$]

>>> k = np.fft.fftfreq(200,2/200)
>>> k
array([  0. ,   0.5,   1. ,   1.5,   2. ,   2.5,   3. ,   3.5,   4. ,
...
-4., -3.5,  -3. ,  -2.5,  -2. ,  -1.5, -1. ,  -0.5])

由上例可以看出k[2]=1,k[6]=3。与2.1示例中频谱吻合。

DFT变换中，频率的分辨率为$\frac{f_s}{N}=\frac{1}{dn}$

由于频谱X[k]的对称性，输出的k[i]也是对称的，fftfreq输出结果前半部分频率形式为$[\frac{0}{dn},\frac{1}{dn}...]$，但是后半部分为对称的负频率，形式为$[...,-\frac{1}{dn},-\frac{0}{dn}]$。

3.2 实数频谱频率坐标计算函数rfftfreq

与fftfreq功能相似，但是只给出前半部分频率，即正频率。

• `k = np.fft.rfftfreq(N, d=1.0)：根据采样点数N，采样周期d(时间间隔)，计算频谱正频率序列k

  • 参数N为采样点数，及信号数组的长度

  • 参数d为采样周期，即相邻两个采样数据时间间隔，为采样频率的倒数

fftfreq输出的频率数组长度为N

rfftfreq输出的频率数组长度为N//2+1

>>> np.fft.rfftfreq(200,2/200)
array([ 0. ,  0.5,  1. ,  1.5,  2. ,  2.5,  3. ,  3.5,  4. ,  4.5,  5. ,
...        
       45. , 45.5, 46. , 46.5, 47. , 47.5, 48. , 48.5, 49. ,49.5, 50. ])

3.3 移动频率顺序

离散傅里叶计算得到的频谱X[k]，以及fftfreq得到的频率都是从0开始排序的。

使用fftshift函数可以把0频率放在正中间，即把[0,1,2,…,…,-2,-1]形式数据调整为[…-3,-2,-1,0,1,2,…]

• np.fft.fftshfit(x):把fft计算的频谱或者fftfreq计算的频率，按照0频率在中间的方式排列

>>> f=np.array([0,1,2,3,-3,-2,-1])
>>> np.fft.fftshift(f)     #移动频率
array([-3, -2, -1,  0,  1,  2,  3])
>>>
>>> X=np.array([1j,2j,3j,4j,5j])  #假设X为fft计算得到的频谱
>>> np.fft.fftshift(X)            #移动频谱顺序，与fftfreq得到的频率移动顺序对应
array([0.+4.j, 0.+5.j, 0.+1.j, 0.+2.j, 0.+3.j])

• np.fft.ifftshift(x)：fftshift的逆向操作

>>> f=np.array([-3, -2, -1,  0,  1,  2,  3])
>>> np.fft.ifftshift(x)
f=np.array([-3, -2, -1,  0,  1,  2,  3])

---

Numpy系列目录

---

个人总结，部分内容进行了简单的处理和归纳，如有谬误，希望大家指出，持续修订更新中。

修订历史版本见：https://github.com/hustlei/AI_Learning_MindMap

未经允许请勿转载。