一直认为凸透镜是标准的圆弧,今天特模拟了下标准圆弧的焦点,下面直接上图吧。



由此可见凸透镜看起来不是标准的圆弧或者椭圆的圆弧。
下面是菲涅尔透镜原理图。
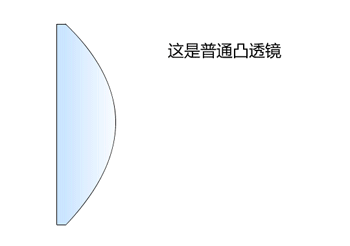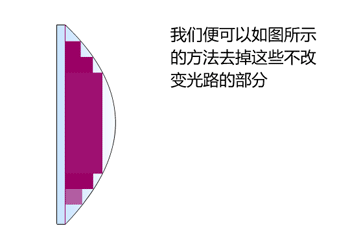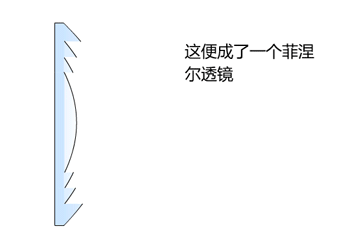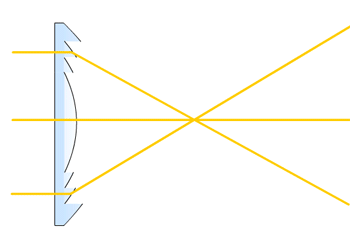
下面开始探讨下理想的凸透镜(所有光线都聚焦到一个点)到底是什么样的曲线。
按照光程差相等, 得出理想的凸透镜是一个双曲线方程, 如下:

![]()
其中:n为折射率,f为焦距,d为透镜厚度。
下面是仿真效果:

证明

可以证明透镜上的任何一点(x,y),满足
条件sin(θ2)=n*sin(θ1), tan(θ1)=-1/y',其中θ1是入射角,θ2是出射角。
可以得到:tan(θ2-θ1)=y/(f-x),或f=x+y/tan(θ2-θ1) 及所有的出设光线都满足在焦点(f,0)处汇集。
证明:
1. 一阶导数:y'=f'(x), 先只考虑x<=d, y>0的部分.

2. 由折射率可得:sin(θ2)=n*sin(θ1), tan(θ1)=-1/y'
3. fx = x + y/tan(θ2-θ1), 化简可得:
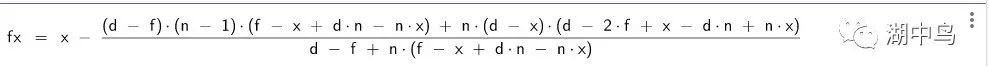
进一步化简可得:
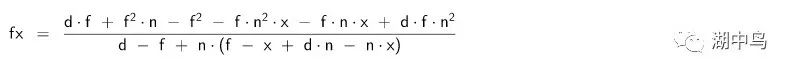
提取公因数可得:

显然, fx = f.(上式分子上的为笔误,应该为
)
由此证明对于任意一点(x, y),满足 x + y/tan(θ2-θ1) = f, 及所有平行光线都满足在(f, 0)处汇集。
下载链接链接:百度网盘 请输入提取码, 提取码关注“湖中鸟”公众号, 发送"提取码“即可获取。
或扫码关注“湖中鸟”









 本文探讨了理想凸透镜的形状,并通过光程差相等的原理推导出其为双曲线方程。文中提供了详细的数学证明过程,并附有仿真效果及菲涅尔透镜原理图。
本文探讨了理想凸透镜的形状,并通过光程差相等的原理推导出其为双曲线方程。文中提供了详细的数学证明过程,并附有仿真效果及菲涅尔透镜原理图。
















 381
381

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








