【算法设计zxd】第3章 求解方程的近似算法 非线性——二分法（穿根），牛顿法（切线），线性代数

目录

非线性方程：

非线性方程的收敛性和收敛速度：

 建立迭代方程

【例3-5】求9x^2-sin x-1=0，在(0,1)之间的解，要求| 9x^2-sin x-1|<0.00001。

二分法：（穿根法）

 二分法的时间渐近复杂度分析

【例3-5】求9x^2-sin x-1=0，在(0,1)之间的解，要求| 9x^2-sin x-1|<0.00001。

牛顿法--有点儿化曲为直那意思

线性代数方程：

 【例3-8】求下列解线性方程组的解

---

非线性方程：

非线性方程的收敛性和收敛速度：

定义 3.1 设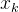是方程 f(x) =0 的根，若存在 x k 的一个邻域 Δ，当 初值属于 Δ时，迭代收敛，则称该迭代过程具有局部收敛性。

定义3.2 设 为第k次迭代的迭代误差，若 【第k+1次迭代误差 与 第k次迭代误差的p次方 同阶。】

则称迭代是 p阶收敛的。称c 为渐近误差常数。

定义 3.3 称 为效率指数，其中，θ表示每次迭代的 计算量， p 表示迭代的收敛阶。

定理 3.1 若当 x ∈ [a, b] 时， φ(x) ∈ [a, b] ，且 φ(x)满足 |φ’(x)| ≤ L<1, x ∈ [a, b]

则迭代收敛于唯一的根。

 建立迭代方程 <