学习使用MATLAB-实现比例、惯性、积分、比例微分、比例积分环节信号仿真

最近在上<<自动控制原理>>，如同听天书，在做完典型电路实物实验后，想用MATLAB做仿真看能不能实现，一方面加深对理论知识的理解，另一方面顺便学习MATLAB软件的使用。
话不多说，这就开始搭建

比例

比例环节传递函数为
$$G(s)=-\frac{z_2}{z_1}=-\frac{R2}{R1}$$
其搭建simulink过程如下

如图首先点击库浏览器,在搜索栏中搜索step,找到如③所示的阶跃信号源，长按拖动至界面里。
像这样操作依次放置一个(step)阶跃信号源,两个(gain)两个比例放大器，一个(scope)示波器。

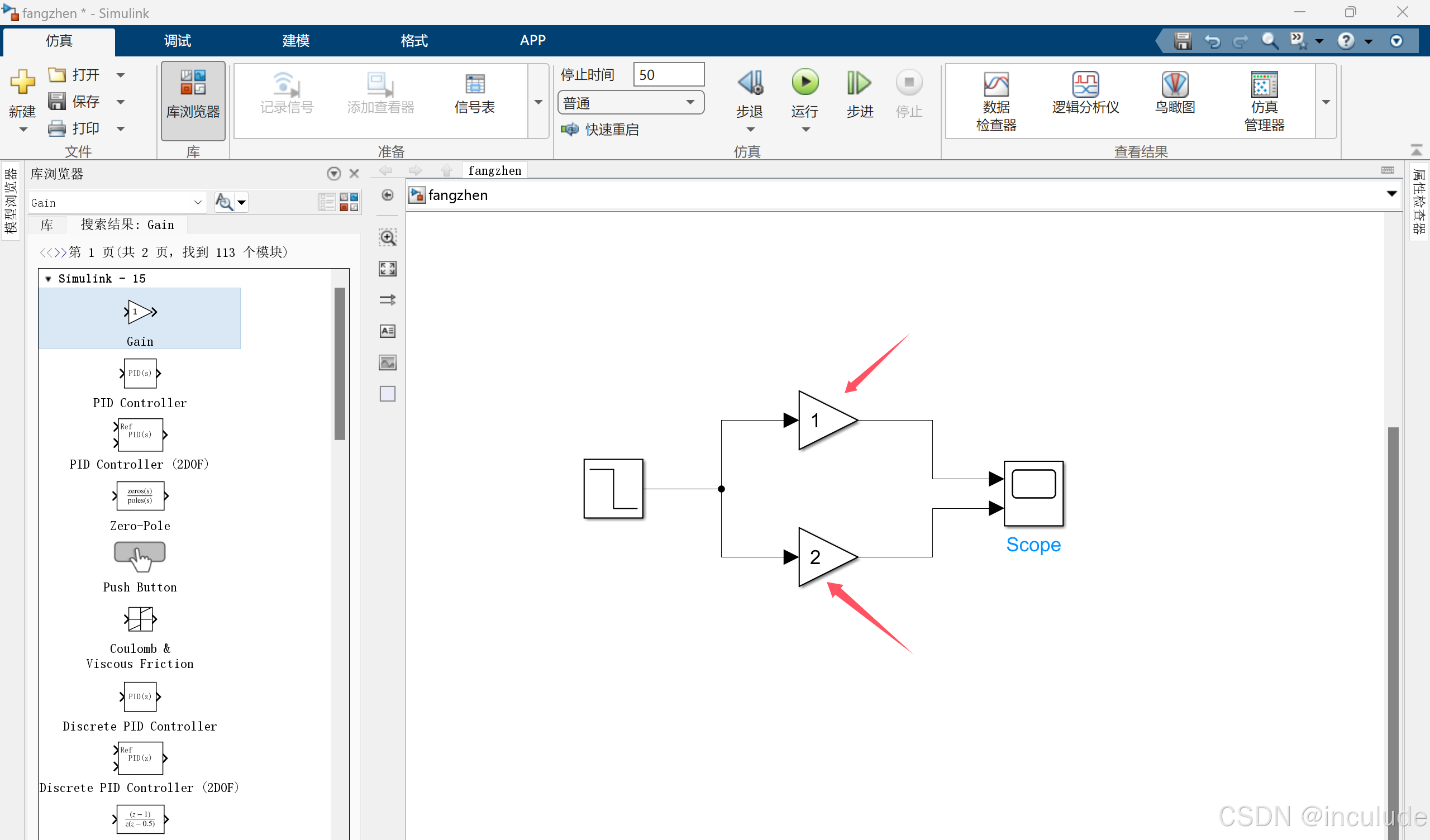
设置比例放大器的放大增益倍数，我这里设置了一个二倍，和一个一倍，也就是不放大，再用导线将其按图中所示连接。

点击运行，双击示波器，现象如下图。

蓝色为，二倍放大增益，黄色为一倍放大增益。

惯性

惯性环节传递函数为
$$G(s)=-\frac{z_2}{z_1}=-\frac{R_2/R_1}{R_2{C}_{1}s}$$
其搭建simulink过程如下

步骤与搭建比例电路大致相同，不同的是需要放置一个Transfer Fcn,

双击这个模块，可以进行调参，系数为降幂排列。
完事点击运行，双击示波器，现象如下图。

积分

积分环节传递函数为
$$G(s)=-\frac{z_2}{z_1}=-\frac{1}{R_2{C}_{1}s}$$
其搭建simulink过程如下
在惯性的基础上进行修改，对Transfer Fcn这个模块进行操作。

配置参数像我这样。点击运行，双击示波器观察到现象如下图。

比例微分

比例微分环节传递函数为
$$G(s)=-\frac{z_2}{z_1}=-R_1{C}_{1}s$$
很简单，就是把比例增益和微分模块串联起来。
需要用到一个微分模块，Derivative

运行现象如下图所示

比例积分

比例积分环节传递函数为
$$G(s)=-\frac{z_2}{z_1}=-\frac{R_2+1/C_1}{R_1}$$
将比例和积分串联

现象如下图

利用MATLAB图像功能显示Simulink的数据

这个时候有个问题，Simulink示波器显示的波形，只能看个大概，没法进一步分析数据，比如我想看比例积分这个图，他在1.2秒时，Y轴所对应的数据，没法看，但MATLAB里的显示的图像能够使用鼠标点击曲线，具体显示点的X,Y轴数据。所以在这里，记录下Simulink与MATLAB的联系。

这里以比例积分作为例子，目的是将比例积分在Simulink生成的图像在MATLAB中显示，并导出图片。

对刚刚比例积分的线路进行适当修改，给示波器添加一个采样通道，方便后续进行对比。

双击示波器，在弹出的界面，点击视图，点击配置属性

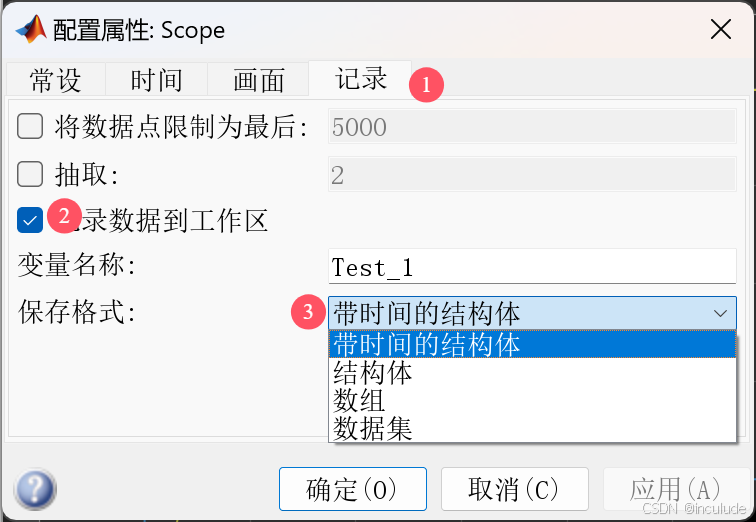
点击记录，勾选记录数据到工作区，保存格式选择带时间的结构体。变量名称我这里写的是Test_1。
完成上述操作，在Simulink界面点击运行即可。
回到MATLAB界面。

在右侧的工作区，找到名称为out，旁边的值写着1X1 SimulationOutput。双击下去。

弹出如此界面，找到我们刚刚写的名称为Test_1的变量。

time记录的是时间。
signals记录的是数值。
这里以signals为例子，往下点。

显示出这个表格，1字段记录的是响应，2字段记录的是输入信号。为什么我会知道，你点击去就知道了。这里我双击点进1字段。

红框所框起来的，便是存储响应数据的结构体。等会需要用到。

接着回到编辑器。

编写这五行程序，

A1=out.Test_1.time;             %将时间数据赋值给A1
B1=out.Test_1.signals(1).values;%将响应数据赋给B1

A2=out.Test_1.time;             %将时间数据赋给A2
B2=out.Test_1.signals(2).values;%将响应数据赋给B2

%在一个图里作两条曲线
%以A1为横轴，以B1为纵轴。
%以A2为横轴，以B2为纵轴。
plot(A1,B1,A2,B2);

点击运行，结果如下图所示。