2023: [Usaco2005 Nov]Ant Counting 数蚂蚁
Time Limit: 4 Sec Memory Limit: 64 MBSubmit: 281 Solved: 183
[ Submit][ Status][ Discuss]
Description
有一天,贝茜无聊地坐在蚂蚁洞前看蚂蚁们进进出出地搬运食物.很快贝茜发现有些蚂蚁长得几乎一模一样,于是她认为那些蚂蚁是兄弟,也就是说它们是同一个家族里的成员.她也发现整个蚂蚁群里有时只有一只出来觅食,有时是几只,有时干脆整个蚁群一起出来.这样一来,蚂蚁们出行觅食时的组队方案就有很多种.作为一头有数学头脑的奶牛,贝茜注意到整个蚂蚁群由T(1≤T≤1000)个家族组成,她将这些家族按1到T依次编号.编号为i的家族里有Ni(1≤Ni≤100)只蚂蚁.同一个家族里的蚂蚁可以认为是完全相同的.
如果一共有S,S+1….,B(1≤S≤B≤A)只蚂蚁一起出去觅食,它们一共能组成多少种不同的队伍呢?注意:只要两支队伍中所包含某个家族的蚂蚁数不同,我们就认为这两支队伍不同.由于贝茜无法分辨出同一家族的蚂蚁,所以当两支队伍中所包含的所有家族的蚂蚁数都相同时,即使有某个家族换了几只蚂蚁出来,贝茜也会因为看不出不同而把它们认为是同一支队伍. 比如说,有个由3个家族组成的蚂蚁群里一共有5只蚂蚁,它们所属的家族分别为1,1,2,2,3.于是出去觅食时它们有以下几种组队方案:
·1只蚂蚁出去有三种组合:(1)(2)(3)
·2只蚂蚁出去有五种组合:(1,1)(1,2)(1,3)(2,2)(2,3)
·3只蚂蚁出去有五种组合:(1,1,2)(1,1,3)(1,2,2)(1,2,3)(2,2,3)
·4只蚂蚁出去有三种组合:(1,2,2,3)(1,1,2,2)(1,1,2,3)
·5只蚂蚁出去有一种组合:(1,1,2,2,3)
你的任务就是根据给出的数据,计算蚂蚁们组队方案的总数.
Input
第1行:4个用空格隔开的整数T,A,S,B.
第2到A+1行:每行是一个正整数,为某只蚂蚁所在的家族的编号.
Output
输出一个整数,表示当S到B(包括S和B)只蚂蚁出去觅食时,不同的组队方案数.
注意:组合是无序的,也就是说组合1,2和组合2,1是同一种组队方式.最后的答案可能很大,
你只需要输出答案的最后6位数字.注意不要输出前导0以及多余的空格.
Sample Input
3 5 2 3
1
2
2
1
3
Sample Output
10
经典题
题意:给你n个集合,第i个集合中有cnt[i]个完全相同的数,总共有p个数(p=∑cnt[i]),要从这p个数中取m个数,然后将这m个数排个序,问能得到多少种不同的序列
dp[i][j]表示前i个集合取j个数的种类数
可以得出转移方程
其中第一维可以滚动数组
如果直接暴力的话复杂度为O(p²)
如果对第二维求前缀和复杂度为O(np)
#include<stdio.h>
#include<algorithm>
using namespace std;
#define mod 1000000
int cnt[1005], sum[1005], dp[2][100005], sd[100005];
int main(void)
{
int ans, n, m, a, b, x, i, j, k, y;
scanf("%d%d%d%d", &n, &m, &a, &b);
for(i=1;i<=m;i++)
{
scanf("%d", &x);
cnt[x]++;
}
for(i=1;i<=n;i++)
sum[i] = sum[i-1]+cnt[i];
dp[0][0] = 1;
for(i=0;i<=m;i++)
sd[i] = 1;
for(i=1;i<=n;i++)
{
y = i&1;
for(j=0;j<=sum[i];j++)
{
dp[y][j] = ((sd[j]-sd[j-min(cnt[i],j)-1])%mod+mod)%mod;
/*for(k=min(cnt[i],j);k>=0;k--)
dp[y][j] = (dp[y][j]+dp[y^1][j-k])%mod;*/
}
sd[0] = dp[y][0];
for(j=1;j<=m;j++)
sd[j] = (sd[j-1]+dp[y][j])%mod;
}
ans = 0;
for(i=a;i<=b;i++)
ans = (ans+dp[n&1][i])%mod;
printf("%d\n", ans);
return 0;
}
/*
3 5 1 5
1
1
2
2
3
*/







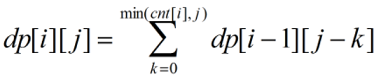














 616
616

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








