样本均值的分布及中心极限定理

样本均值的分布及中心极限定理

样本均值的分布：

设X1，X2，X3，....Xn为从某一总体中抽出的随机样本，因此X1，X2，X3，....Xn为互相独立且与总体有相同分布的随机变量。现在要知道样本均值的分布（反复抽样，样本均值当然会服从一定的分布），首先要知道总体的分布。

当总体分布服从正太分布N（μ，σ2），样本均值的分布将服从：

上面的公式表明，的期望值与总体均值相同，而方差则缩小为总体方差的1/n。这说明当用样本均值去估计总体均值时，平均来说没有偏差，当n越来越大时，的散布程度越来越小，即用估计μ越来越准确。然而实际情况是，总体的分布并不总是正太分布或近似正太分布，此时的的分布也将取决于总体分布的情况。值得庆幸的是，当抽样个数n比较大时，人们证明了中心极限定理：设从均值为μ，方差为σ2的任意一个总体中抽取样本量为n的样本，当n充分大时，样本均值的抽样分布近似服从均值为μ，方差为σ2/n的正太分布。

公式推导过程：

1. 的推导过程：

样本均值=平均值，因此可以将n提取出来：

样本均值的分布，由于是反复抽样，因此可以推导：

当n足够大时：

2. 的推导过程：

已经方差公式为：

样本均值方差公式：

将上一步获取的样本均值 带入：

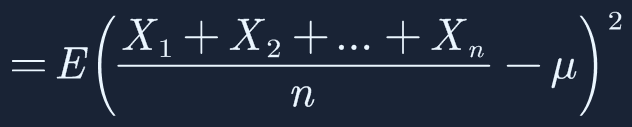
提取出n:

合并后：

因为抽样样本是独立同分布的，因此协方差=0：

化简后：

实际案例：

某台灯供应商声称其生产的台灯具有均值为60个月，标准差为6个月的寿命分布。现假设质检部门决定检验该厂的说法是否正确，为此随机抽取50个该厂生产的台灯进行寿命检验。

1. 假定厂商声称是正确的，试求出50个台灯的平均寿命的抽样分布。

2. 假定厂商声称是正确的，则50个样本组成的样本的平均寿命不超过57个月的概率为多少？

1.根据中心极限定理可以推出50个台灯的平均寿命近似服从正太分布，其均值μ=60，方差σ2=62/50=0.72，σ=0.85。

即：

2.假定厂商声称是正确的，则50个样本组成的样本的平均寿命不超过57个月的概率为：

假定厂商声称是正确的，则50个台灯的平均寿命不超过57个月的概率为0.0002。概率这么低，根据小概率事件原理，肯定不可能发生了。相反，如果真的观测到50个台灯的平均寿命低于57个月，则有理由怀疑厂方说法的正确性。