二维随机变量

最新推荐文章于 2023-09-25 16:36:38 发布

UserOrz

最新推荐文章于 2023-09-25 16:36:38 发布

阅读量5k

点赞数 3

分类专栏：概率论文章标签：概率论

本文链接：https://blog.csdn.net/jdsaiasodh/article/details/115427222

版权

13 篇文章 0 订阅

订阅专栏

设 $E$ 是一个随机试验，它的样本空间是 $S=\{e\}$ ，设 $X = X (e)$ 和 $Y = Y (e)$ 是定义在 $S$ 上的随机变量

由他们构成的一个向量 $(X, Y)$ 叫做二维随机向量或二维随机变量

设 $(X, Y)$ 是二维随机变量，对于任意实数 $x, y$ ，二元函数：

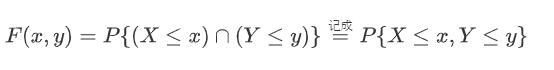
称为二维随机变量 $(X, Y)$ 的分布函数，或称为随机变量 $X$ 和 $Y$ 的联合分布函数

$F (x, y)$ 是变量 $x$ 和 $y$ 的不减函数，即对于任意固定的 $y$ ，当 $x_2>x_1$ 时 $F(x_2,y) \ge F(x_1,y)$ ，对固定的 $x$ 同理
$\le F(x,y) \le 1$ ， $F(-\infty,\infty) = 0$ ， $F(\infty,\infty) = 1$
对于任意固定的 $y$ ， $F(-\infty,y)=0$ ，对于任意固定的 $x$ ， $F(x,-\infty)=0$
$F (x + 0, y) = F (x, y)$ ， $F (x, y + 0) = F (x, y)$ ，即 $F (x, y)$ 关于 $x$ 和 $y$ 右连续
对于任意的 $x_1,y_1)$ ， $x_2,y+2)$ ， $x_1 < x_2$ ， $y_1 < y_2$ 有： $\\P\{x_1 < X \le x_2,y_1 < Y \le y_2\} = F(x_2,y_2) - F(x_2,y_1) - F(x_1,y_2) + F(x_1,y_1) \ge 0$

设二维随机变量 $(X, Y)$ 所有可能取的值为 $x_i,y_i)$ ， $1,2,\cdots$

我们称 $P(X=x_i,Y=y_i) = p_{ij}$ ， $i, j = 1, 2, . . .$ ，为二维离散型随机变量 $(X, Y)$ 的分布率

记 $P(X=x_i,Y=y_i) = p_{ij}$ ， $i, j = 1, 2, . . .$ ，则由概率的定义有 $p_{ij} \ge 0$ ， $\sum_{i=1}^{\infty} \sum_{j=1}^{\infty} p_{ij} = 1$

设二维随机变量 $(X, Y)$ 所有可能取的值为 $x_i,y_i)$ ， $1,2,\cdots$

$\sum_{i=1}^{x} \sum_{j=1}^{y} p_{xy}$

对于二维随机变量 $(X, Y)$ 的分布函数 $F (x, y)$ 如果存在非负可积函数 $f (x, y)$ 使得对于任意 $x, y$ 有

$\int_{-\infty}^y \int_{-\infty}^x f(u,v) dudv$

则称 $(X, Y)$ 是二维连续性随机变量，函数 $f (x, y)$ 称为二维连续性随机变量 $(X, Y)$ 的概率密度，或称为随机变量 $X$ 和 $Y$ 的联合概率密度

$\ge 0$
$\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} f(x,y) dxdy = F(\infty,\infty) = 1$
设 $G$ 是 $x O y$ 平面上的区域，点 $(X, Y)$ 落在 $G$ 内的概率为 $P\{(X,Y) \in G\} = \iint_G f(x,y)dxdy$
若 $f (x, y)$ 在点 $(x, y)$ 连续，则有 $\frac{\partial^2F(x,y)}{\partial x \partial y} = f(x,y)$

$\int_{-\infty}^y \int_{-\infty}^x f(u,v) dudv$

$\{(X,Y) \in G\} = \int\int_G(x,y)dxdy$

均匀分布 $\left\{\begin{aligned}& \frac{1}{S} ，(x,y) \in D \\&0 \qquad ,其他\end{aligned}\right.$

二维正态分布

在这里插入图片描述

关注