方程自己解（1）——物理信息神经网络（PINN）

最新推荐文章于 2025-03-11 16:15:42 发布

留小星

最新推荐文章于 2025-03-11 16:15:42 发布

阅读量5.7w

点赞数 128

分类专栏： PINN 文章标签：神经网络深度学习机器学习 PINN

本文链接：https://blog.csdn.net/jerry_liufeng/article/details/120727393

版权

PINN 专栏收录该内容

5 篇文章

订阅专栏

本文介绍了物理信息神经网络（PINN）的基本概念和工作原理，它结合了神经网络的自动微分特性与物理方程，用于解决偏微分方程的求解问题。PINN通过将物理方程的残差纳入损失函数，使模型训练兼顾物理规律。文章以连续时间模型和离散时间模型为例，展示了PINN在薛定谔方程、Allen-Cahn方程、Navier-Stokes方程和KdV方程等典型问题上的应用，验证了其准确性和有效性。PINN作为一种数据驱动的方法，为物理问题的数值模拟提供了新的思路。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

文章目录

（一）前言

最近正在看利用“深度学习”解方程（大概吧，其实只是利用了neural network的自动微分特性（AD）），在看一些文章的同时，将文章中提到的开源代码用起来和复现一些基本方程求解能够加快我学习的进度，这里将持续贴出一些方程和代码的求解过程。当然非常希望同学和朋友们可以给我指出错误，最后如果能够坚持下去，这个系列的工作会分享到github，同时如果对各个开源程序有所帮助那就更好了！
由于会参考到很多文章，所以将这个系列当作一个读文章的过程也很不错。

（二）物理神经网络（PINN）解读

1. PINN基本背景

2019年，布朗大学应用数学系研究团队提出了PINN，并发表在《计算物理学期刊》(Journal of Computational Physics)。自从发表，PINN成为了AI物理领域最常见的一个关键词。从下图可见，当前的引用量已经达到了1674。

在这里插入图片描述

figure cite：Google scholar

2. 算法描述

PINN，即物理信息神经网络，也就是将物理方程作为限制加入到神经网络之中使得拟合得到的结果更加满足物理规律。这个限制如何实现呢？也就是将物理方程迭代前后的差值就爱到Neural Network中的损失函数之中，让这个物理方程每次都能够得到训练。那么神经网络在训练迭代的过程之中优化的就不仅仅是网络自己的损失函数，还包括了物理方程每次迭代的差值，使得最后训练出来的模型满足某种设定的物理规律。

3. PINN文章解读

考虑下面的问题：
$u_t + N(u;\lambda) = 0 \tag{1}$
其中， $u (x, t)$ 是要求的解， $N(u;\lambda)$ 是关于这个解的非线性操作算子（比如偏导数）， $\lambda$ 是待定参数。
那么问题就来了：

Data-driven solutions of partial differential equations：参数 $\lambda$ 已知的时候，如何求的未知的解 $u (x, t)$
Data-driven discovery of partial differential equations：参数 $\lambda$ 未知的时候，如何求解 $u (x, t)$ 的同时确定参数 $\lambda$

3.1 连续时间模型

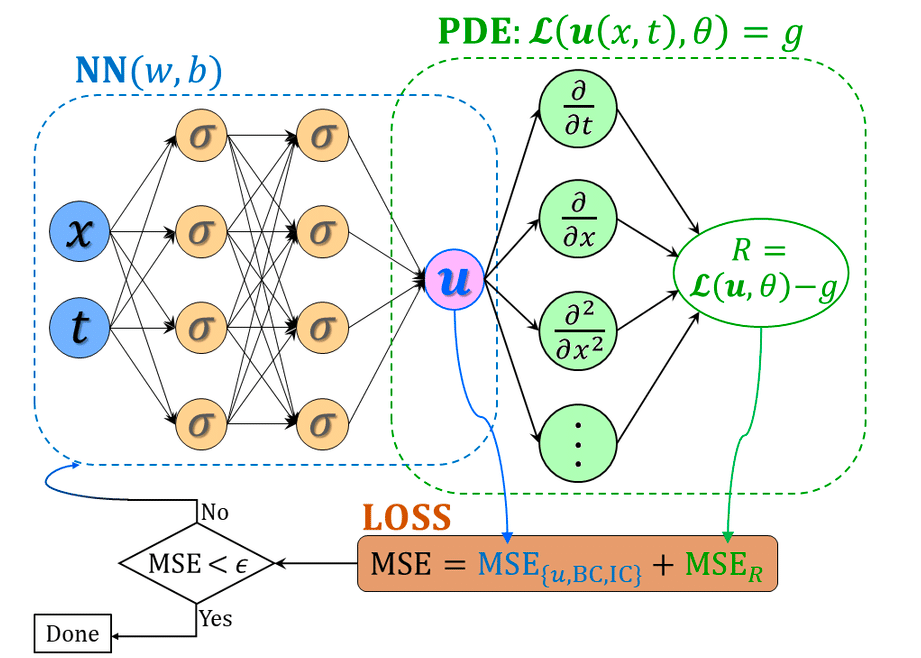
在这里插入图片描述

figure cite:https://bbs.huaweicloud.com/blogs/detail/263776
$u_t + N[u] \tag{2}$
使用神经网络来逼近 $u (x)$ 和 $f (x)$ ，且这两个网络共享参数，（基于神经网络自动微分的功能，链式法则）（这个点我在后面会用一个简单的例子来说明）

具体操作：首先定义一个网络来拟合u(x)，然后 $f (t, x)$ 可以接在 $u (x, t)$ 的后面再加上一些操作算子。为了优化网络我们定义一个均方损失函数：
$MSE_u + MSE_f \tag{3}$

其中
$MSE_u = \frac{1}{N_u}\sum_{i=1}^{N_u}\vert u(t_u^i,x_u^i) - u^i \vert ^2 \tag{4}$

$MSE_f = \frac{1}{N_f}\sum_{i=1}^{N_f}\vert u(t_f^i,x_f^i) \vert ^2 \tag{5}$

式子4表示在初始和边界条件处神经网络的拟合值 $u(t_u^i,x_u^i)$ 与真实值的均方误差；
式子5表示的是神经网络与真实物理规律的均方误差。

3.2 离散时间模型

=这个数学有些强硬，待到做到后面有机会回来补充！！！=
假设有一个q阶的龙格-库塔方程（百度百科-龙格库塔法）:
$u^{n+c_i} = u^n - \Delta \sum_{j=1}^{q}a_{ij}N[u^{n+c_j}] , \; i=1,....,q$ $u^{n+1} = u^n - \Delta \sum_{j=1}^{q}b_{j}N[u^{n+c_j}] \tag{6}$
这里 $u^{n+c_j}(x) = u(t^n +c_j\Delta t,x) , \; j = 1，2.,...,q$ .这个通用形式通过参数 ${a_{ij} , b_j,c_j\}$ 融合了显式和隐式的解，那么式7可以表示为下面简单的形式
$u^n = u_i^n , \; i = 1，...,q$ $u^n = u^{n}_{q+1} \tag{7}$

我们首先设计一个多输出的神经网络拟合
$u^{n+c_1}(x)，...,u^{n+c_q}(x),u^{n+1}(x)]$

然后这个先验假设结果和方程7就构成了一个物理信息神经网络：
$[u^{n}_1(x)，...,u^{n}_q(x),u^{n}_{q+1}(x)]$

3.3 论文结果展示

（1） Schrodinger equation：薛定谔方程
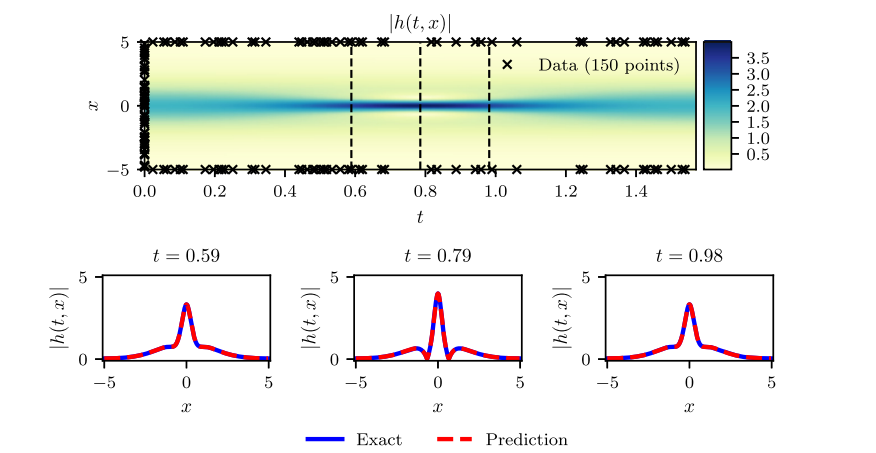
在这里插入图片描述
figure cite: (M.Raissi.etc,Journal of Computational Physics,2019)

顶部是 $∣ h (t, x) ∣$ 沿着初始和边界条件的训练数据份分布，以及随机生成的20000个采样点序列；下面是精确数值解和我们神经网络预测的结果的对比图，红色表示预测结果，蓝色是精确解。此处对应的L2误差（最小二乘误差）是 $1.97 . 10^{-3}$

（2） Allen-Cahn方程：
在这里插入图片描述

figure cite: (M.Raissi.etc,Journal of Computational Physics,2019)

（3） Navier-Stokes方程(什么是纳维-斯托克斯方程？)：
在这里插入图片描述

figure cite: (M.Raissi.etc,Journal of Computational Physics,2019)

(4) KdV 方程：
在这里插入图片描述

4. 总结

详细内容参考原文，因为我认为读这篇文章的关键是：

Why?
PINN:物理信息神经网络是在神经网络通用近似理论的基础上，通过加入偏导数等算子给数值模拟加上了物理约束，从而使得整个网络具有模拟物理规则的作用。关键点在于：通用近似理论 + 物理信息的传递（导数算子+残差构建）+NN的自动微分（AD）
How？
怎么构建网络去优化？简单的全连接神经网络甚至已经能很好地进行通用近似了！！！
What?
用PINN可以做什么？解偏微分方程，在各种不同的领域中都有涉及。对于我个人而言，我在读地球物理，其中的波动方程、程函方程、格林函数等等都是有待攻克的领域，当然也已经有很多人有了很多的发现，但是基于前人研究也会有更多的见解

参考：
【1】博客分析：物理神经网络（PINN）解读
【2】PINN论文：Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations
【3】当神经网络遇上物理: PINNs原理解析