感觉了解插值就像是打怪一样,现在终于打到这个终极大boss了。插值最后一篇。
上一篇我们讲了cubic interpolation(三次插值),这一篇我们来讲bicubic interpolation(双线性插值)
双三次插值:是二维空间中最常用的插值方法。在这种方法中,函数 f在点 (x,y) 的值可以通过矩形网格中最近的十六个采样点的加权平均得到,在这里需要使用两个多项式插值三次函数,每个方向使用一个。之前我们说cubic interpolation是求4n个未知数,两个cubic interpolation将会16n个未知数。
方法一
比如说我们的图片最开始是2*2的,我们如果要把图片放大2倍,变成4*4,那么放大后,有些像素肯定是没有,这就要借助于其他的已知的点。
它的计算公式为:
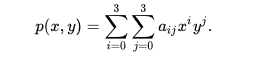
假设 fx.fy fxy是函数f的偏导和全导,并且知道了4个点的值(0,0),(0,1),(1,0),(1,1)。我们现在就是要求aij。一个16个系数。那和我们上一篇讲的cubic interpolation一样,我们几威要6个方程式。
1 点带入

2 偏导

3 全导

一共16个。
向量![]()
是我们要求的。
向量![]()
是我们已知的。
假设![]() A为已知矩阵
A为已知矩阵

方法二
还可以这样子求a向量,在叫做权重。
用公式计算
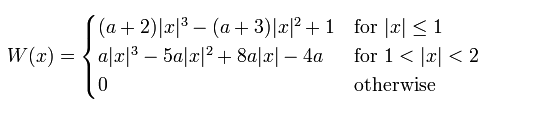
一般a取-0.5或者-0.75
我们要做的就是求出BiCubic函数中的参数x,从而获得上面所说的16个像素所对应的权重W(x)。BiCubic基函数是一维的,而像素是二维的,所以我们将像素点的行与列分开计算。f(X,Y)像素值为:

好,就此我就总结完我所有的学到插值。
下面是我参考和学习的一些网站,主要看的是第一个英文文档
https://en.wikipedia.org/wiki/Bicubic_interpolation
https://www.jianshu.com/p/055706fd32ee
https://zhuanlan.zhihu.com/p/62860859
























 227
227

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








