先做一个声明:文章是由我的个人公众号中的推送直接复制粘贴而来,因此对智能优化算法感兴趣的朋友,可关注我的个人公众号:启发式算法讨论。我会不定期在公众号里分享不同的智能优化算法,经典的,或者是近几年提出的新型智能优化算法,并附MATLAB代码。
蜣螂优化(DBO)算法:
“今天介绍的这个算法,应该是目前最新的一个群智能优化算法。实际上,一个周以前我就看到了,但是没有去深入了解和学习。昨天对它的原始参考文献进行了仔细阅读,并编码实现了这个算法,应该说,这个算法的收敛性能还是非常优越的!
这里再啰嗦一句,蜣螂,就是屎壳郎!翻译成蜣螂优化,会显得高大尚些,档次一下就有了,要是来个屎壳郎算法,就太不文雅了……”
蜣螂优化(Dung Beetle Optimizer, DBO)算法是2022年11月27日提出的,大家可以算算到今天才提出多久。它是由东华大学的沈波教授团队提出的一种全新的群智能优化算法。或许大家对这个团队不是很了解,但相信大家对麻雀搜索算法(Sparrow Search Algorithm, SSA)一定不陌生。著名的SSA就是由这个团队提出,感兴趣的同学可以进一步跟踪一下。
DBO算法的原始参考文献如下:
“Xue J, Shen B. Dung beetle optimizer: a new meta-heuristic algorithm for global optimization[J]. The Journal of Supercomputing, 2022: 1-32.”
01
灵感来源
蜣螂是自然界常见的昆虫,以动物的粪便为食。学过生物的同学都知道,它们在自然界中扮演着分解者的角色,这意味着它们在生态系统中至关重要。蜣螂有一个有趣的习惯,就是把粪便打成球状,然后滚出来,如图1所示。

图1 蜣螂的滚球行为
一方面,蜣螂会尽可能快速地移动它们的粪球,这样可防止被其他蜣螂竞争;另一方面,蜣螂会利用天体线索(特别是太阳、月亮和偏振光)来导航,使粪球沿直线滚动。然而,如果没有了光源(即完全黑暗),蜣螂的路径就不再是直线,而是弯曲的,有时甚至略圆。一些自然因素(如风和不平整的地面)也会导致蜣螂偏离原来的方向。此外,蜣螂在滚动粪球时很可能遇到障碍物,无法前进。此时,蜣螂会爬到粪球上跳舞(包括一系列的旋转和停顿),这也决定了它们新的运动方向。(这里我想好奇地问一下,你能想象一个东西站在粑粑上跳舞的画面吗)
蜣螂收获的粪球主要有两个目的:1) 一些粪球用来产卵和养育下一代;2) 其余的用作食物。具体来说,蜣螂把粪球埋起来,雌性蜣螂在这些粪球里产卵。粪球不仅是幼虫的发育场所,还为幼虫提供了生活所必需的食物。
另外,一些蜣螂会从其他蜣螂那里掠夺粪球,作者将它们称作小偷,如图2所示,这也是自然界中很常见的现象。

图2 蜣螂中的小偷掠夺粪球
基于蜣螂的这些行为,作者提出了DBO算法,主要灵感就来自于蜣螂的滚球、跳舞、觅食、偷窃和繁殖行为。准确来说,应该叫蜣螂优化器。
02
算法设计
如上所述,作者对蜣螂的滚球、跳舞、觅食、偷窃和繁殖行为进行数学建模。DBO算法主要包括四个过程:滚球、繁殖、觅食和偷窃。与前几期推送一样,目前我还不会在公众号里编辑数学公式。因此,这部分内容在Word文档里先写好,然后做成图片,最后导入。




由此,作者便提出了基于蜣螂滚球、跳舞、觅食、偷窃和繁殖行为的DBO算法。简单地说,DBO算法也是基于子种群的,每个子种群执行不同的搜索方式。与蛇优化(SO)和蜉蝣算法(MA)不同的是,DBO算法不是基于双种群的,而是基于多个子种群,作者划分了四个子种群。
03
计算流程
由于DBO算法将种群中的蜣螂划分成了四种不同的角色,因此它的计算流程会相对复杂一些,需要执行滚球、繁殖、觅食和偷窃四种算子。这里我用伪代码给出了它的计算流程,如图7所示。

图7 DBO算法计算流程
04
实验仿真
DBO算法到今天才提出两周不到,因此我非常好奇它的性能。这里对DBO算法的收敛性能进行了简单的测试。在编码中,所有参数按照它原始文献的取值进行设置,种群规模N为30,最大迭代次数T也与原文一致,等于500,问题维度D我选取的30。
这里以多峰函数Ackley、Levy和单峰函数Zakharov为例,展示DBO算法在30维环境下的收敛效果,如图8所示。这里就不再进一步做分析了。
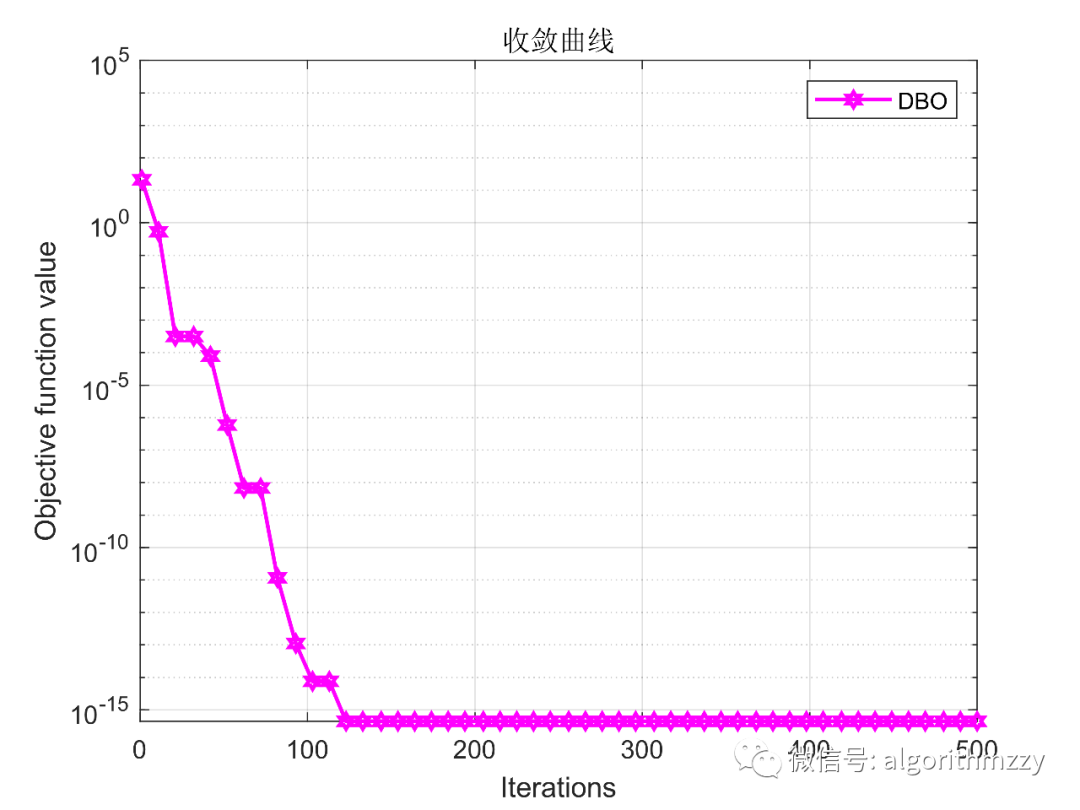
(a) Ackley

(b) Levy

(c) Zakharov
图8 DBO算法的收敛曲线
05
MATLAB代码
公众号:启发式算法讨论
























 921
921

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










