使用田口实验获取优化算法的参数最优组合

先做一个声明：文章是由我的个人公众号中的推送直接复制粘贴而来，因此对智能优化算法感兴趣的朋友，可关注我的个人公众号：启发式算法讨论。我会不定期在公众号里分享不同的智能优化算法，经典的，或者是近几年提出的新型智能优化算法，并附MATLAB代码。

停更了四个多月，愿大家一切安好！感谢老粉一直都在，我会努力抽空更新。

先说一下田口实验的目的：获得你所设计算法的参数的最优组合。比如，你设计了某某优化算法，包含四个需要初始化参数：α、β、γ、δ，每个参数都有几个不同的可选值，例如α是在[0.01, 0.02, 0.03, 0.04]中选一个带入算法。那么，这些参数值就有多种组合，具体哪个是最优的呢？这就可以使用田口实验来确定，然后将实验得到的参数最优组合设置进算法即可。

Part1 为什么叫“田口”

（这部分可以不用看，与具体的实验没啥关系。）

日本的田口玄一（Genichi Taguchi）博士在参数设计方法方面贡献非常突出，他在设计中引入了“信噪比”（Signal to Noise Ratio, SN Ratio）的概念，并以此作为评价参数组合优劣的一种测度，以至于很多文献和软件都把稳健参数设计方法称为田口设计（Taguchi Design）。

田口设计（Taguchi design)，或称稳健参数设计，是通过选择可控因子的水平组合来减少系统(或过程）对噪声变化的敏感性，从而减少系统性能波动的一种统计方法。所以，它最开始不是用来获得算法的参数设置的，但是我们可以采用它的原理来获取进化算法的最优参数。

Part2 田口实验的具体流程

这部分直接讲实验过程，可以只看这部分。

1 建立正交表

正交表是一组完整规则的设计表格，可以减少实验次数，提高测试效率。比方对于一个三因素三水平的实验来说，共需要进行3^3＝27种组合的全面实验，但是如果利用正交表，只需要进行3^2=９次实验就能反映出全面实验的情况。这里先解释什么叫“三因素三水平”，意思就是有三个参数，每个参数有三个可选取值，即每个参数有三种水平。例如，假设PSO算法有种群规模(NP)、个人学习因子(c1)和社会学习因子(c2)三个参数，每个参数有四个可选取值，则称为“三因素四水平”。然后，正交表可以使用Excel或者SPSS直接生成。SPSS在线免费网址：https://spssau.com/indexs.html。以“三因素三水平”为例，正交表生成过程如下：

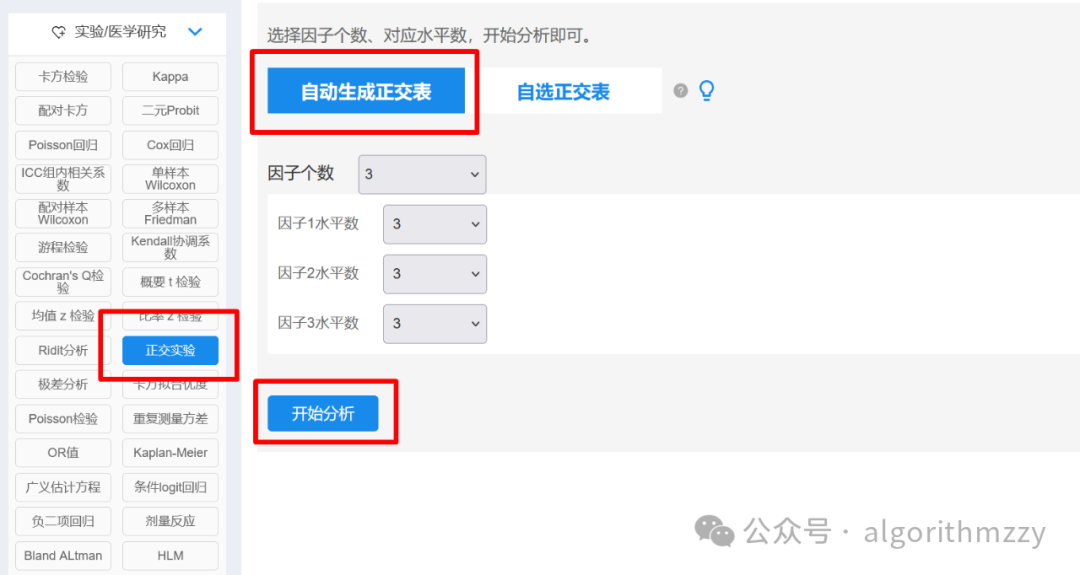
最终，得到正交表如下：

正交设计表
编号	因子1	因子2	因子3
1	1	1	1
2	1	2	3
3	1	3	2
4	2	1	3
5	2	2	2
6	2	3	1
7	3	1	2
8	3	2	1
9	3	3	3

将正交表里面的123转换成参数的具体取值，就得到9组不同的参数组合。例如，假设GA有种群规模(NP)、交叉率(Pc)和变异率(Pm)三个参数，每个参数有三个水平（即三个不同的取值），具体为：NP=[100, 150, 200]，Pc=[0.7, 0.8, 0.9]，Pm=[0.01, 0.02, 0.03]。则将参数对应的具体水平（取值）带入上表，得到9种不同的参数组合，如下表所示。

正交设计表
编号	种群规模（NP）	交叉因子（Pc）	变异因子（Pm）
1	100	0.7	0.01
2	100	0.8	0.03
3	100	0.9	0.02
4	150	0.7	0.03
5	150	0.8	0.02
6	150	0.9	0.01
7	200	0.7	0.02
8	200	0.8	0.01
9	200	0.9	0.03

因此，需要将这9种参数组合分别带入算法进行实验。换言之，就是让你将这“9种算法”进行对比实验。具体的实验设置可以和平时的对比实验一样，即设置算法最大迭代次数为多少多少，算法独立运行多少次啥的。这里只需要记录一个值就行，可以是多次运行的最优值，也可以是均值或者误差均值。记录一个就够了，不用记录多个。

2 计算响应值

（我看一些文献叫的响应值，这个不重要，不影响实验的）

我们假设：有10个Benchmark，然后每个算法（每组参数）在每个算例上独立运行20次，记录的是20次运行的均值。那么，就有10个均值，因为有10个Benchmark。进一步，一个算法（一组参数）对应的结果就应该是这10个均值的均值。如下表所示：

编号	因子1	因子2	因子3	响应值
1	1	1	1	197.6
2	1	2	3	198.8
3	1	3	2	199.5
4	2	1	3	199.3
5	2	2	2	200.3
6	2	3	1	198.8
7	3	1	2	200.6
8	3	2	1	199.6
9	3	3	3	200.6

当然，也不一定是均值，这里可以自己设计的。响应值可以自己看着选，只不过对于进化算法，均值用得更多而已。你也可以记录20次运行的最优值或中位数等等，然后再计算这10个结果的最优值作为响应值。只要言之有理即可。

得到每组参数的响应值后，接下来，就可以知道每个参数在每个水平下的响应度（为了与响应值区分，我这里叫的响应度）。因为每个参数的每个水平在表中都出现了3次，即每个水平都有三个算法采用。进一步计算每个水平的三组实验结果的均值就得到了该水平的响应情况。如下表所示（也就是将上表转换为下表）：

	因子1(NP)	因子2(Pc)	因子3(Pm)
水平 1	198.6	199.2	198.7
水平 2	199.5	199.7	200.1
水平 3	200.3	199.6	199.6
极差	1.7	0.5	1.4
重要水平	1	3	2

当然，也不一定算均值，也可使用最优值啥的。例如这篇文章“https://mi5g.com/article/1507264?q=s&t=52061”使用的是平均相对百分比偏差。然后，选择每个参数具有最小响应度的水平（取值）作为该参数值即可。如上表所示，种群规模(NP)设置为水平1，即100；交叉率(Pc)设置为水平1，即0.7；变异率(Pm)设置为水平1，即0.01。所以，最佳的参数组合就是[NP, Pc, Pm]=[100, 0.7, 0.01]。（注意，我这里的数据都是随便给的，恰好三个参数的最佳设置都是水平1而已）

最后，上面这张表不是后面还有两行吗。这是用来进一步确定参数的灵敏度或者重要性的。计算每个参数下，三个水平的响应度的极差，即最大值减去最小值，然后根据极差大小，确定参数的重要性。根据上表结果，三个参数在相比之下，种群规模(NP)对算法影响最大，交叉率(Pc)对算法影响最小。这两行是用来增加描述的，论文能多写几句话罢了，可以没有。

3 画图

（就是把上面那个表转化成图片，方便观察，这个是必须有的）

最后，画出每个参数的响应图，横坐标为参数的取值，纵坐标为响应值。类似于下图（我这里是举例子而已，与上面的表格数据不对应）：

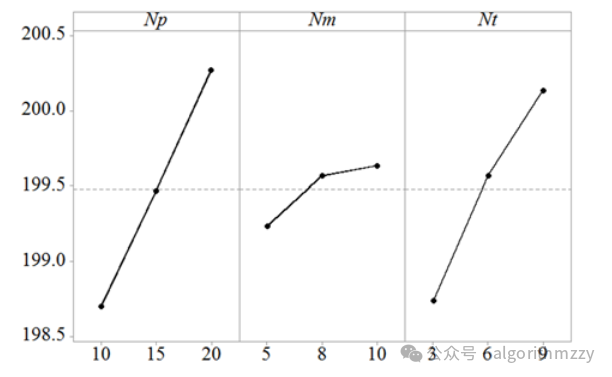
观察图片，就可以一眼看出参数的最佳取值。就上面这张图片来讲，Np最佳取值是10，Nm最佳取值是5，Nt最佳取值是3。所以，最佳的参数组合就是[Np, Nm, Nt]=[10, 5, 3]。将这组参数带入算法，就得到了最终的算法。

Part3 田口实验的几点说明

1.参数的数量和参数的水平数最好相同。即，三因素三水平，四因素四水平，以此类推。这样做的目的是方便建立正交表，以及后续的响应值计算。我很少看到参数数量和水平数不相等的文章。

当然，只要你能接受并且能操作，这个可以自己定。以“六因素三水平”为例，最后的参数响应图诸如下图：

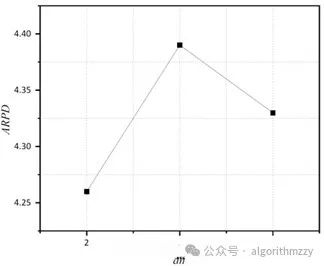
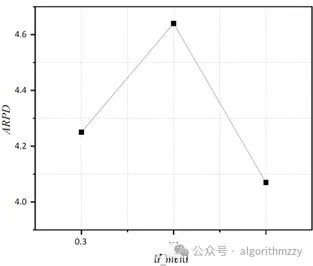
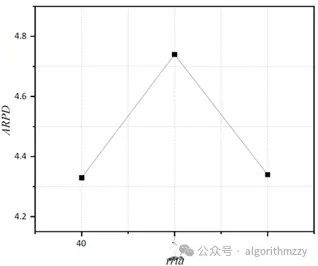
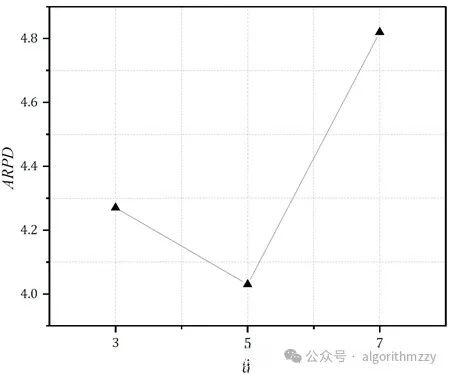
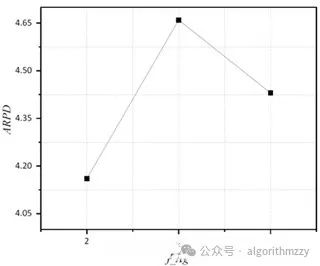
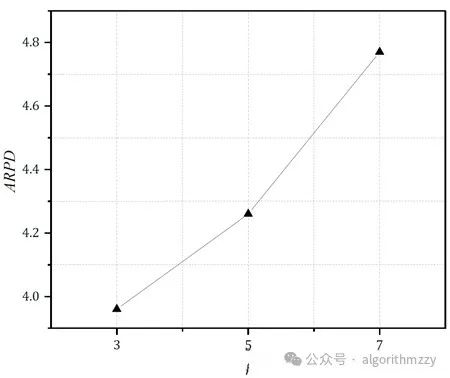
2.参数的几个候选值是自己给定的。相比于直接设置参数值而言，田口实验会相对更科学，毕竟是科学实验得出的参数最优组合。审稿人一般不会追着问你0.7和0.8之间还有没有更好的值。这样问属于抬杠。但是如果直接设置参数值的话，很可能被追问。所以，田口实验还是能做就做。

3.不用纠结一些具体的名称，诸如响应值、响应度啥的，只需要知道实验流程即可。不要因为个别不重要的名称来抬杠。

4.田口实验的算例不一定使用整个测试套件，你可以选择最复杂的一个或者具有代表性的某几个。另外，响应值可以自己设计，言之有理即可。但建议对看看文献，和其他文献保持一致，别整得不同不样，花里胡哨的。

5.图是必须有的，表是可以没有的。因为这个实验不是用来验证算法的有效性，只是确定参数的最优组合。因此不一定要把正交表这些列出来，可以叙述实验流程，最后把图片画出来，给出结论即可。