画线算法 - Bresenham原理及Java实现

Bresenham是绘制线段最有效率的算法之一,该算法仅仅使用整型加减及字节位操作运算 (省去了用于计算斜率的除法运算)，因而计算效率非常高。其实现也非常的简单明了。本文以Java代码为例，一步一步由浅而深的讲解了Bresenham算法的完整实现。

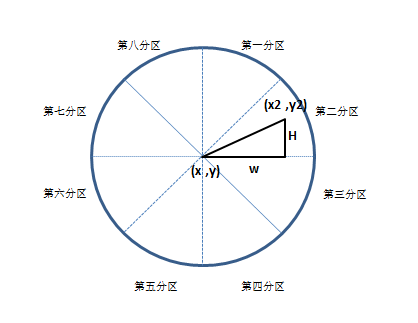
下图所示，二维坐标系统可均分为八个分区，作为本文例子的线段（x，y，x2，y2）位于第二分区。

在实现该算法之前，我们先看看最原始，最直观的做法。该原始算法可以帮助更好的阐述布氏算法，因为布氏算法本身就是该原始算法的扩展和优化。

    public void drawLineRaw(int x, int y, int x2, int y2, int color) {
        int w = x2 - x;
        int h = y2 - y;
        double m = h / (double) w;
        double j = y;
        for (int i = x; i <= x2; i++) {
            drawPixel(i, (int) j, color);
            j += m;
        }
    }

该实现尽管效率低，但实现了我们需要的功能。注意！上面代码实际只能画位于第二分区的线条，而不能画位于其它分区的线条。当耐心读完本文，在结尾部分我们会看到覆盖所有分区的完整的实现。

操作m = h / w，j + = m实际上是增加了分子，并保持分母不变。当分子h变得等于或大于分母w，分子减去分母并将j增加1（实现该操作对应的代码为(int) j）。 这阐述了Bresenham算法的基本原理，Bresenham算法用整数加法取代了除法和实数操作。如下代码为Bresenham算法在第二分区的实现。(该部分是理解全文的关键，请仔细体会)

      public void drawIn2ndOctant(int x,int y,int x2,int y2,int color) {
              int w = x2 - x;
              int h = y2 - y;
              int dy1 = -1;
              int fastStep = Math.abs(w);
              int slowStep =Math.abs(h);
              int numerator = fastStep>> 1;
              for (int i = 0; i <=fastStep; i++) {
                     drawPixel(x,y, color);
                     numerator+= slowStep;
                     if (!(numerator <fastStep)) {
                           numerator-= fastStep;
                           y+= dy1;
                     }
                     x++;
              }
       }

注意， int numerator = fastStep >> 1; 分子等于快速变量的一半，该步骤让y值的四舍五入在中间点而不是在整数点。

一个完整的画线功能将需要考虑所有的分区， 那我们是否需要8份如上所示的代码呢？答案是不，其它八个分区的实现都十分相似，并很容易通用化。首先，我们来看看在不同的八分区的相似之处。 在第三分区线段只是第二分区线段基于Y方向的镜像，因此只需设置dy1 = 1，而不是dy1=-1。请参见下面的第4行的区别。

       public void drawIn3rdOctant(int x,int y,int x2,int y2,int color) {
              int w = x2 - x;
              int h = y2 - y;
              int dy1 = 1;
              int fastStep = Math.abs(w);
              int slowStep = Math.abs(h);
              int numerator = fastStep>> 1;
              for (int i = 0; i <=fastStep; i++) {
                     drawPixel(x,y, color);
                     numerator+= slowStep;
                     if (!(numerator <fastStep)) {
                           numerator-= fastStep;
                           y+= dy1;
                     }
                     x++;
              }
       }

在第六分区和第三分区的实现是基本相同的，除了基于坐标轴的镜像。这可以通过改变代码 x++为x- - ​​来实现。 简单吧！

       public void drawIn6thOctant(int x,int y,int x2,int y2,int color) {
              int w = x2 - x;
              int h = y2 - y;
              int dy1 = 1;
              int fastStep = Math.abs(w);
              int slowStep = Math.abs(h);
              int numerator = fastStep>> 1;
              for (int i = 0; i <=fastStep; i++) {
                     drawPixel(x,y, color);
                     numerator+= slowStep;
                     if (!(numerator <fastStep)) {
                           numerator-= fastStep;
                           y+= dy1;
                     }
                     x--;
              }
       }

这同样适用于第七分区与第二分区。可以通过改变行x ++为x–​​来实现。

    public void drawIn7thOctant(int x,int y,int x2,int y2,int color) {
              int w = x2 - x;
              int h = y2 - y;
              int dy1 = -1;
              int fastStep = Math.abs(w);
              int slowStep = Math.abs(h);
              int numerator = fastStep>> 1;
              for (int i = 0; i <=fastStep; i++) {
                     drawPixel(x,y, color);
                     numerator+= slowStep;
                     if (!(numerator <fastStep)) {
                           numerator-= fastStep;
                           y+= dy1;
                     }
                     x--;
              }
        }

重复，重复… 重构！如下是一个通用于第二，第三，第六和第七分区的线段绘制功能。

    public void drawInEvenOctant(int x,int y,int x2,int y2,int color) {
              int w = x2 - x;
              int h = y2 - y;
              int dx1 = w < 0 ? -1: (w > 0 ? 1 : 0);
              int dy1 = h < 0 ? -1: (h > 0 ? 1 : 0);
              int dx2 = 0;
              int dy2 = dx2 = w < 0? -1 : (w > 0 ? 1 : 0);

              int fastStep = Math.abs(w);
              int slowStep = Math.abs(h);
              int numerator = fastStep>> 1;
              for (int i = 0; i <=fastStep; i++) {
                     drawPixel(x,y, color);
                     numerator+= slowStep;
                     if (!(numerator <fastStep)) {
                           numerator-= fastStep;
                           x+= dx1;
                           y+= dy1;
                     }else {
                           x+= dx2;
                           y+= dy2;
                     }
              }
       }

到目前为止，我们实现的第二，第三，第六,第七分区的画线功能。然而，这仍然不完整。我们发现位于第一，第四，第五，和第八分区具有一个共同的区别，其高度的变化快于宽度的变化，而在第二，第三，第六，和第七分区的线段，其宽度的变化快于高度的变化。综合该逻辑，如下是Bresenham算法的对所有的八分区画线的完整实现。

      public void drawLine(int x0,int y0,int x1,int y1,int color) {
              int x = x0;
              int y = y0;

              int w = x1 - x0;
              int h = y1 - y0;

              int dx1 = w < 0 ? -1: (w > 0 ? 1 : 0);
              int dy1 = h < 0 ? -1: (h > 0 ? 1 : 0);

              int dx2 = w < 0 ? -1: (w > 0 ? 1 : 0);
              int dy2 = 0;

              int fastStep = Math.abs(w);
              int slowStep = Math.abs(h);
              if (fastStep <=slowStep) {
                     fastStep= Math.abs(h);
                     slowStep= Math.abs(w);

                     dx2= 0;
                     dy2= h < 0 ? -1 : (h > 0 ? 1 : 0);
              } 
              int numerator = fastStep>> 1;

              for (int i = 0; i <=fastStep; i++) {
                     drawPixel(x,y, color);
                     numerator+= slowStep;
                     if (numerator >=fastStep) {
                           numerator-= fastStep;
                           x+= dx1;
                           y+= dy1;
                     }else {
                           x+= dx2;
                           y+= dy2;
                     }
              }
       }

本文主要参考自http://tech-algorithm.com/articles/drawing-line-using-bresenham-algorithm/， 并结合实际的游戏引擎，Java实现代码有一定优化。希望对你有所帮助！ 反馈请联系jinbing.peng@yahoo.com.