Sanders, O. (2021). Improving Revocation for Group Signature with Redactable Signature. In: Garay, J.A. (eds) Public-Key Cryptography – PKC 2021. PKC 2021. Lecture Notes in Computer Science(), vol 12710. Springer, Cham. https://doi.org/10.1007/978-3-030-75245-3_12
前置文献https://blog.csdn.net/jiongxv/article/details/125254302?spm=1001.2014.3001.5502
可撤销群签名
Introduction
文章的主要内容:
- 具有时间限制键的群签名的概念。首先,我们扩展了这个概念,以允许高粒度撤销:成员的签名密钥可以在某些时刻停用,然后自动恢复。
- 证明了使用可编校签名实际上很容易实现这个复杂的属性。
- 在此背景下考虑了PKC 20中最近的一种可编校签名方案,我们通过大幅减少公钥的大小来改进该方案
Redactable Signatures with Linear Size Public Key
前置文献效率上的问题:将redacted messages 聚合在一个元素中(即Derive中的
σ
1
′
\sigma_1'
σ1′),通过附加元素(Derive中的
σ
2
′
\sigma_2'
σ2′)这个过程是诚实的。
不幸的是,在前置文献中,这是通过在公钥中添加一个二次数(以n为单位)的元素(即
Z
i
,
j
Z_{i,j}
Zi,j)来实现的,这很快就会变得低效
构造:使用PS-签名的一个特例:
-
s
k
:
=
(
x
,
y
)
sk:=(x,y)
sk:=(x,y),对消息
{
m
i
}
i
=
1
n
\{m_i\}_{i=1}^n
{mi}i=1n的签名
(
σ
1
,
σ
2
)
=
(
h
,
h
x
+
∑
i
=
1
n
y
i
⋅
m
i
)
∈
G
1
2
(\sigma_1,\sigma_2)=(h,h^{x+\sum_{i=1}^ny^i\cdot m_i})\in\mathbb{G}_1^2
(σ1,σ2)=(h,hx+∑i=1nyi⋅mi)∈G12。对应原始PS签名的验证变成:
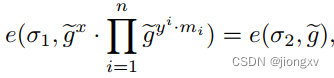
相应地,改进的Redactable签名的Derive σ 1 ′ \sigma_1' σ1′定义变为 σ ~ ← ∏ i ∈ I ˉ g ~ y i ⋅ m i \widetilde{\sigma}\leftarrow\prod_{i\in\bar{\mathcal{I}}}\widetilde{g}^{y^i\cdot m_i} σ ←∏i∈Iˉg yi⋅mi,verify的条件1变为:
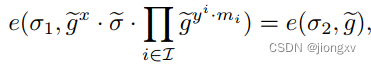
新的安全性保证:
类似地需要考虑安全性,确保
σ
~
\widetilde{\sigma}
σ
没有被用来聚合非法的元素。改进的Redactable签名中的解决方法在这里的特例中是不管用的,因为使用了特殊的
p
s
k
psk
psk,并且它包含了一个
O
(
n
2
)
O(n^2)
O(n2)元素的公钥造成了效率问题。
原本的解决方法:
σ
2
=
∏
i
∈
I
,
j
∈
I
ˉ
Z
i
,
j
m
j
=
(
g
∑
j
∈
I
ˉ
y
j
⋅
m
j
)
∑
i
∈
I
y
i
\sigma_2=\prod_{i\in\mathcal{I},j\in\bar{\mathcal{I}}}Z_{i,j}^{m_j}=(g^{\sum_{j\in \bar{\mathcal{I}}}y_j\cdot m_j})^{\sum_{i\in\mathcal{I}} y_i}
σ2=∏i∈I,j∈IˉZi,jmj=(g∑j∈Iˉyj⋅mj)∑i∈Iyi
e
(
g
∑
j
∈
I
ˉ
y
j
⋅
m
j
,
g
~
∑
i
∈
I
y
i
)
=
e
(
(
g
∑
j
∈
I
ˉ
y
j
⋅
m
j
)
∑
i
∈
I
y
i
,
g
~
)
=
e
(
σ
2
,
g
~
)
e(g^{\sum_{j\in\bar{\mathcal{I}}}y_j\cdot m_j},\widetilde{g}^{\sum_{i\in\mathcal{I}}y_i})=e((g^{\sum_{j\in\bar{\mathcal{I}}}y_j\cdot m_j})^{\sum_{i\in\mathcal{I}}y_i},\widetilde{g})=e(\sigma_2,\widetilde{g})
e(g∑j∈Iˉyj⋅mj,g
∑i∈Iyi)=e((g∑j∈Iˉyj⋅mj)∑i∈Iyi,g
)=e(σ2,g
)
新的解决办法:
- 注意:对于一个诚实的
σ
~
\widetilde{\sigma}
σ
,有:
G = e ( ∏ i ∈ I g y n + 1 − i , σ ~ ) = e ( ∏ i ∈ I g y n + 1 − i , ∏ j ∈ I ˉ g ~ y j ⋅ m j ) = e ( g ∑ i ∈ I , j ∈ I ˉ y n + 1 − i + j ⋅ m j , g ~ ) \begin{aligned} G&=e(\prod_{i\in\mathcal{I}}g^{y^{n+1-i}},\widetilde{\sigma})\\ &=e(\prod_{i\in\mathcal{I}}g^{y^{n+1-i}},\prod_{j\in\bar{\mathcal{I}}}\widetilde{g}^{y^j\cdot m_j})\\ &=e(g^{\sum_{i\in\mathcal{I},j\in\bar{\mathcal{I}}}y^{n+1-i+j} \cdot m_j},\widetilde{g}) \end{aligned} G=e(i∈I∏gyn+1−i,σ )=e(i∈I∏gyn+1−i,j∈Iˉ∏g yj⋅mj)=e(g∑i∈I,j∈Iˉyn+1−i+j⋅mj,g )
中间可以看做 2 n − 1 2n-1 2n−1个元素 g y i , i ∈ [ 1 , n ] ∪ [ n + 2 , 2 n ] g^{y^i},i\in[1,n]\cup[n+2,2n] gyi,i∈[1,n]∪[n+2,2n](中间没有 n + 1 n+1 n+1是因为 i ≠ j i\neq j i=j,没有 2 n + 1 2n+1 2n+1是因为此时 I = ϕ \mathcal{I}=\phi I=ϕ,那就不需要derive了),添加到公钥中。 - 根据改进的Redactable签名可以试图总结出一个理论:即一个不规范的
σ
~
\widetilde{\sigma}
σ
必然导致一个(公共密钥中没有提供的)包含
g
y
n
+
1
g^{y^{n+1}}
gyn+1或
g
x
⋅
y
u
,
u
>
0
g^{x·y^u},u>0
gx⋅yu,u>0形式的元素的配对
G
G
G。(
g
y
n
+
1
g^{y^{n+1}}
gyn+1出现表示
I
ˉ
\bar{\mathcal{I}}
Iˉ和
I
\mathcal{I}
I有重合,
x
x
x表示其他不合法的项)
不幸的是,这是不正确的。当 G G G是由不规范的 σ ~ ← ∏ i ∈ [ 1 , n ] g ~ y i ⋅ m i ′ \widetilde{\sigma}\leftarrow\prod_{i\in[1,n]}\widetilde{g}^{y^i\cdot m_i'} σ ←∏i∈[1,n]g yi⋅mi′计算而来(比如存在 i ∈ I , m i ′ ≠ 0 i\in\mathcal{I},m_i'\neq 0 i∈I,mi′=0:
G = e ( g ∑ u = 1 2 n y u ⋅ a u , g ~ ) , a n + 1 = ∑ i ∈ I m i ′ \begin{aligned} G &=e(g^{\sum_{u=1}^{2n}y^u \cdot a_u},\widetilde{g}),a_{n+1}=\sum_{i\in\mathcal{I}}m_i' \end{aligned} G=e(g∑u=12nyu⋅au,g ),an+1=i∈I∑mi′
敌手选择 m i ′ m_i' mi′值是容易的,使抵消 y n + 1 y^{n+1} yn+1的系数 a n + 1 a_{n+1} an+1。在这种情况下,可以只使用公钥中给出的元素 g y i , i ∈ [ 1 , n ] ∪ [ n + 2 , 2 n ] g^{y^i},i\in[1,n]\cup[n+2,2n] gyi,i∈[1,n]∪[n+2,2n]创建伪造 - 在系数
a
n
+
1
a_{n+1}
an+1中添加一些不可预测性,以阻止这个攻击:生成hash输出
c
i
←
H
(
σ
1
∣
∣
σ
2
∣
∣
σ
~
∣
∣
I
∣
∣
i
)
,
i
∈
I
c_i\leftarrow {\rm H}(\sigma_1||\sigma_2||\widetilde{\sigma}||\mathcal{I}||i),i\in\mathcal{I}
ci←H(σ1∣∣σ2∣∣σ
∣∣I∣∣i),i∈I,计算另一种配对:
G = e ( ∏ i ∈ I g y n + 1 − i ⋅ c i , σ ~ ) = e ( g ∑ i ∈ I , j ∈ I ˉ y n + 1 − i + j ⋅ c i ⋅ m j , g ~ ) \begin{aligned} G&=e(\prod_{i\in\mathcal{I}}g^{y^{n+1-i}\cdot c_i},\widetilde{\sigma})\\ &=e(g^{\sum_{i\in\mathcal{I},j\in\bar{\mathcal{I}}}y^{n+1-i+j} \cdot c_i\cdot m_j},\widetilde{g}) \end{aligned} G=e(i∈I∏gyn+1−i⋅ci,σ )=e(g∑i∈I,j∈Iˉyn+1−i+j⋅ci⋅mj,g )
①不存在 y n + 1 y^{n+1} yn+1,保证了 I ∩ I ˉ = ϕ \mathcal{I\cap\bar{I}}=\phi I∩Iˉ=ϕ;
②如果存在不规范的 σ ~ \widetilde{\sigma} σ ,那么 y n + 1 y^{n+1} yn+1的系数是 ∑ i ∈ I c i ⋅ m i ′ \sum_{i\in\mathcal{I}}c_i\cdot m_i' ∑i∈Ici⋅mi′;由于 c i c_i ci依赖于 σ ~ \widetilde{\sigma} σ (包含 m i ′ m_i' mi′),任何选择标量的 m i ′ m_i' mi′使 a n + 1 = 0 a_{n+1}=0 an+1=0的策略都不太可能成功,因为 m i ′ m_i' mi′的任何变化都会造成 { m i } i ∈ I \{m_i\}_{i\in\mathcal{I}} {mi}i∈I的变化
注意:不能直接从消息 m i m_i mi中派生出 c i c_i ci,因为这样会妨碍对 m i m_i mi知识的有效证明,而只能从签名的第一个元素 ( σ 1 , σ 2 , σ ~ ) (\sigma_1,\sigma_2,\widetilde{\sigma}) (σ1,σ2,σ )中得出 c i c_i ci。
scheme
一种不可链接的,Redactable 签名,其中公钥是线性的。

注意
Y
i
Y_i
Yi中
i
i
i的范围,这么定义是为了
公钥中不再有二次项
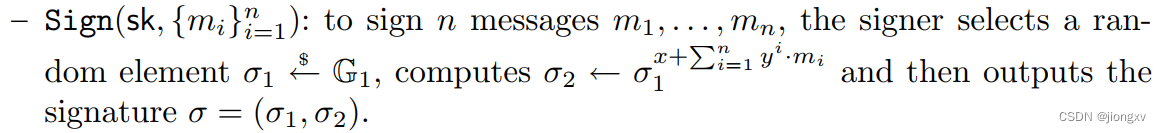
除了对应公私钥的变化,签名方式和改进的Redactable签名方案中一致

σ
1
′
,
σ
2
′
,
σ
~
′
\sigma_1',\sigma_2',\widetilde{\sigma}'
σ1′,σ2′,σ
′与原方案的前三条一致。
然后对所有的
i
∈
I
i\in\mathcal{I}
i∈I,计算
c
i
←
H
(
σ
1
∣
∣
σ
2
∣
∣
σ
~
∣
∣
I
∣
∣
i
)
c_i\leftarrow {\rm H}(\sigma_1||\sigma_2||\widetilde{\sigma}||\mathcal{I}||i)
ci←H(σ1∣∣σ2∣∣σ
∣∣I∣∣i),并生成:
σ
3
′
←
∏
i
∈
I
[
Y
n
+
1
−
i
t
⋅
∏
j
∈
I
‾
Y
n
+
1
−
i
+
j
m
j
]
c
i
\sigma_{3}^{\prime} \leftarrow \prod_{i \in \mathcal{I}}\left[Y_{n+1-i}^{t} \cdot \prod_{j \in \overline{\mathcal{I}}} Y_{n+1-i+j}^{m_{j}}\right]^{c_{i}}
σ3′←∏i∈I[Yn+1−it⋅∏j∈IYn+1−i+jmj]ci
返回
{
m
i
}
i
∈
I
\{m_i\}_{i\in\mathcal{I}}
{mi}i∈I的签名
σ
=
(
σ
1
′
,
σ
2
′
,
σ
3
′
,
σ
~
′
)
\sigma=(\sigma_1',\sigma_2',\sigma_3',\widetilde{\sigma}')
σ=(σ1′,σ2′,σ3′,σ
′)

分析:条件1与原方案相同,是具有不可链接性的,验证了签名
{
m
i
}
i
∈
I
\{m_i\}_{i\in\mathcal{I}}
{mi}i∈I
e
(
σ
1
,
X
~
⋅
σ
~
⋅
∏
i
∈
I
Y
~
i
m
i
)
=
e
(
σ
1
r
,
g
~
x
⋅
g
~
t
⋅
∏
j
∈
I
ˉ
Y
~
j
m
j
⋅
∏
i
∈
I
Y
~
i
m
i
)
=
e
(
σ
1
r
,
g
~
x
⋅
g
~
t
⋅
∏
i
∈
[
1
,
n
]
g
~
y
i
⋅
m
i
)
=
e
(
σ
1
r
,
g
~
t
+
x
+
∑
i
=
1
n
y
i
⋅
m
i
)
=
e
(
σ
2
,
g
~
)
\begin{aligned} e(\sigma_1,\widetilde{X}\cdot\widetilde{\sigma}\cdot\prod_{i\in\mathcal{I}}\widetilde{Y}_i^{m_i})&=e(\sigma_1^r,\widetilde{g}^x\cdot\widetilde{g}^t\cdot\prod_{j\in\bar{\mathcal{I}}}\widetilde{Y}_j^{m_j}\cdot\prod_{i\in\mathcal{I}}\widetilde{Y}_i^{m_i})\\ &=e(\sigma_1^r,\widetilde{g}^x\cdot\widetilde{g}^t\cdot\prod_{i\in[1,n]}\widetilde{g}^{y^i\cdot m_i})\\ &=e(\sigma_1^r,\widetilde{g}^{t+x+\sum_{i=1}^ny^i\cdot m_i})=e(\sigma_2,\widetilde{g})\\ \end{aligned}
e(σ1,X
⋅σ
⋅i∈I∏Y
imi)=e(σ1r,g
x⋅g
t⋅j∈Iˉ∏Y
jmj⋅i∈I∏Y
imi)=e(σ1r,g
x⋅g
t⋅i∈[1,n]∏g
yi⋅mi)=e(σ1r,g
t+x+∑i=1nyi⋅mi)=e(σ2,g
)
条件2:
e
(
σ
3
,
g
~
)
=
e
(
∏
i
∈
I
[
Y
n
+
1
−
i
t
⋅
∏
j
∈
I
‾
Y
n
+
1
−
i
+
j
m
j
]
c
i
,
g
~
)
=
e
(
∏
i
∈
I
[
Y
n
+
1
−
i
t
⋅
∏
j
∈
I
‾
Y
n
+
1
−
i
y
j
⋅
m
j
]
c
i
,
g
~
)
=
e
(
∏
i
∈
I
[
Y
n
+
1
−
i
t
+
∑
j
∈
I
ˉ
y
j
⋅
m
j
]
c
i
,
g
~
)
=
e
(
∏
i
∈
I
Y
n
+
1
−
i
c
i
,
g
~
t
+
∑
j
∈
I
ˉ
y
j
⋅
m
j
)
=
e
(
∏
i
∈
I
Y
n
+
1
−
i
c
i
,
σ
~
)
\begin{aligned} e(\sigma_3,\widetilde{g})&=e(\prod_{i \in \mathcal{I}}\left[Y_{n+1-i}^{t} \cdot \prod_{j \in \overline{\mathcal{I}}} Y_{n+1-i+j}^{m_{j}}\right]^{c_{i}},\widetilde{g})\\ &=e(\prod_{i \in \mathcal{I}}\left[Y_{n+1-i}^{t} \cdot \prod_{j \in \overline{\mathcal{I}}} Y_{n+1-i}^{y^j\cdot m_{j}}\right]^{c_{i}},\widetilde{g})\\ &=e(\prod_{i \in \mathcal{I}}\left[ Y_{n+1-i}^{t+\sum_{j \in \bar{\mathcal{I}}}y^j\cdot m_{j}}\right]^{c_{i}},\widetilde{g})\\ &=e(\prod_{i \in \mathcal{I}}Y_{n+1-i}^{c_{i}},\widetilde{g}^{t+\sum_{j \in \bar{\mathcal{I}}}y^j\cdot m_{j}})=e(\prod_{i \in \mathcal{I}}Y_{n+1-i}^{c_{i}},\widetilde{\sigma})\\ \end{aligned}
e(σ3,g
)=e(i∈I∏⎣⎡Yn+1−it⋅j∈I∏Yn+1−i+jmj⎦⎤ci,g
)=e(i∈I∏⎣⎡Yn+1−it⋅j∈I∏Yn+1−iyj⋅mj⎦⎤ci,g
)=e(i∈I∏[Yn+1−it+∑j∈Iˉyj⋅mj]ci,g
)=e(i∈I∏Yn+1−ici,g
t+∑j∈Iˉyj⋅mj)=e(i∈I∏Yn+1−ici,σ
)
如果
I
∩
I
ˉ
≠
ϕ
\mathcal{I\cap\bar{I}}\neq\phi
I∩Iˉ=ϕ,即存在不规范的
σ
3
\sigma_3
σ3使得
i
=
j
i=j
i=j,等式不成立(因为
c
i
c_i
ci保证了发送方无法谨慎地选择
m
j
≠
0
,
j
∈
I
ˉ
m_j\neq0,j\in\bar{\mathcal{I}}
mj=0,j∈Iˉ使
y
j
y^j
yj的系数抵消);
t
t
t是不可链接性所使用的一个dummy sk。
注意:1)公钥中提供的元素足以计算派生签名,尤其是元素
σ
3
\sigma_3
σ3,因为对于所有
i
∈
I
,
j
∈
I
ˉ
i\in\mathcal{I},j\in\bar{\mathcal{I}}
i∈I,j∈Iˉ,有
n
+
1
−
i
∈
[
1
,
n
]
n+1-i\in[1,n]
n+1−i∈[1,n],
n
+
1
−
i
+
j
∈
[
1
,
n
]
∪
[
n
+
2
,
2
n
]
n+1-i+j\in[1,n]\cup[n+2,2n]
n+1−i+j∈[1,n]∪[n+2,2n]
2)为了便于说明,把
σ
3
\sigma_3
σ3的定义为
∏
i
∈
I
[
Y
n
+
1
−
i
t
⋅
∏
j
∈
I
‾
Y
n
+
1
−
i
+
j
m
j
]
c
i
\prod_{i \in \mathcal{I}}\left[Y_{n+1-i}^{t} \cdot \prod_{j \in \overline{\mathcal{I}}} Y_{n+1-i+j}^{m_{j}}\right]^{c_{i}}
∏i∈I[Yn+1−it⋅∏j∈IYn+1−i+jmj]ci,但发现在大多数情况下直接套用这个公式计算是相当低效的,因为它需要
∣
I
∣
(
n
−
∣
I
∣
+
1
)
|\mathcal{I}|(n-|\mathcal{I}|+1)
∣I∣(n−∣I∣+1)次幂计算。
对于所有的
u
∈
[
1
,
n
]
∪
[
n
+
2
,
2
n
]
u\in[1,n]\cup[n+2,2n]
u∈[1,n]∪[n+2,2n],定义
t
u
=
t
⋅
c
i
t_u=t\cdot c_i
tu=t⋅ci,当
u
=
n
+
1
−
i
,
i
∈
I
u=n+1-i,i\in\mathcal{I}
u=n+1−i,i∈I,其他情况下
t
u
=
0
t_u=0
tu=0。这种情况下
σ
3
′
\sigma_3'
σ3′可写成:
σ
3
′
=
∏
u
∈
[
1
,
n
]
∪
[
n
+
2
,
2
n
]
Y
u
t
u
+
s
u
,
s
u
=
∑
i
∈
I
,
j
∈
I
ˉ
,
j
−
i
=
u
−
n
−
1
c
i
⋅
m
j
\sigma_{3}^{\prime}=\prod_{u \in[1, n] \cup[n+2,2 n]} Y_{u}^{t_{u}+s_{u}},s_u=\sum_{i\in\mathcal{I},j\in\bar{\mathcal{I}},j-i=u-n-1}c_i\cdot m_j
σ3′=u∈[1,n]∪[n+2,2n]∏Yutu+su,su=i∈I,j∈Iˉ,j−i=u−n−1∑ci⋅mj
这样只需要
2
n
−
1
2n-1
2n−1次幂计算。
Group Signature with Time-Bound Keys
具有时间限制密钥的群签名
- G K e y G e n ( 1 λ , n ) → ( g s k , g p k ) {\rm GKeyGen}(1^\lambda,n)\rightarrow(gsk,gpk) GKeyGen(1λ,n)→(gsk,gpk). n n n是时间周期数的一个上界,并初始化一个寄存器 R e g {\rm Reg} Reg
-
J
o
i
n
{\rm Join}
Join.群管理员和一个新的群成员
k
k
k的两方交互协议。
Manager输入: ( g p k , T k , g s k , R e g ) → ( r t k , T k ) (gpk,\mathcal{T}_k,gsk,{\rm Reg})\rightarrow({\rm rt}_k,\mathcal{T}_k) (gpk,Tk,gsk,Reg)→(rtk,Tk),manager在寄存器 R e g [ k ] {\rm Reg}[k] Reg[k]中存储一个revocation token和用户的活动时间段。
user输入: ( g p k , T k ) → u s k k (gpk,\mathcal{T}_k)\rightarrow usk_k (gpk,Tk)→uskk,user获得群签名密钥 u s k k = ( s k k , T k ) usk_k=(sk_k,\mathcal{T}_k) uskk=(skk,Tk)。 - S i g n ( u s k k , g p k , t , m ) → σ {\rm Sign}(usk_k,gpk,t,m)\rightarrow \sigma Sign(uskk,gpk,t,m)→σ,现在的时间周期 t t t。
- R e v o k e ( ( g s k , g p k ) , R e g , t , R ) → R L t {\rm Revoke}((gsk,gpk),{\rm Reg},t,\mathcal{R})\rightarrow {\rm RL}_t Revoke((gsk,gpk),Reg,t,R)→RLt。一组要撤销的用户 R \mathcal{R} R,撤销列表 R L t {\rm RL}_t RLt.
- V e r i f y ( g p k , t , R L t , σ , m ) → 1 / 0 {\rm Verify}(gpk,t,{\rm RL}_t,\sigma,m)\rightarrow 1/0 Verify(gpk,t,RLt,σ,m)→1/0
- O p e n ( g s k , R e g , σ , m , t ) → k / ⊥ {\rm Open}(gsk,{\rm Reg},\sigma,m,t)\rightarrow k/\perp Open(gsk,Reg,σ,m,t)→k/⊥该算法要么返回用户标识符 k k k,要么返回失败消息
Intuition
用前面的Redactable Signature构建具有时间限制密钥的群签名:想在一段时间 T k \mathcal{T}_k Tk内加入加入群的任何用户 k k k收到一个消息 { m i } i = 1 n \{m_i\}_{i=1}^n {mi}i=1n上的redactable 签名(如果 i ≠ T k , m i = 0 i\neq\mathcal{T}_k,m_i=0 i=Tk,mi=0),这就产生了一个非常紧凑的组签名密钥,它基本上由这个签名组成。要在时间段 i i i发布组签名,成员只需在子集 I = i \mathcal{I}= {i} I=i上运行Derive算法,就可以得到修订后的签名 σ ′ \sigma' σ′.验证者可以直接使用后者来检查这个成员在这个时间段是否活跃,因为否则这个签名在0的时候是有效的。
scheme
将上文构建的redactable签名方案记为
Σ
\Sigma
Σ
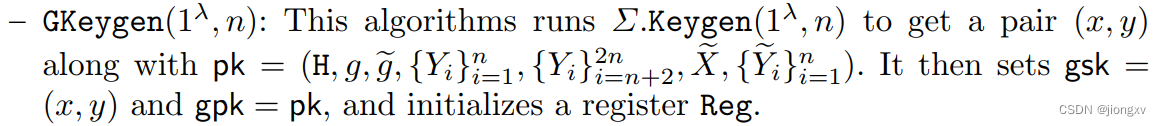
sk,pk是
Σ
\Sigma
Σ签名中的公私钥
−
J
o
i
n
- {\rm Join}
−Join向群管理员登记在
T
k
\mathcal{T}_k
Tk时间内有效的新用户
k
k
k,并返回可验证的签名作为其用户私钥。
\qquad\qquad
新用户
k
(
g
p
k
,
T
k
,
)
k(gpk,\mathcal{T}_k,)
k(gpk,Tk,)
\qquad\qquad\qquad\qquad\qquad
群管理员
(
g
p
k
,
T
k
,
g
s
k
,
R
e
g
)
(gpk,\mathcal{T}_k,gsk,{\rm Reg})
(gpk,Tk,gsk,Reg)
-
新用户 k k k随机选择私钥 s k k ← Z p sk_k\leftarrow\mathbb{Z}_p skk←Zp ———————————— → ( g s k k , g ~ s k k ) \rightarrow(g^{sk_k},\widetilde{g}^{sk_k}) →(gskk,g skk)给群管理员
-
用诸如Schnorr算法证明 s k k sk_k skk的知识———————————— → \rightarrow →如果证明有效,且 e ( g s k k , g ~ ) = e ( g , g ~ s k k ) e(g^{sk_k},\widetilde{g})=e(g,\widetilde{g}^{sk_k}) e(gskk,g )=e(g,g skk),随机选择r
-
\qquad\qquad ( σ 1 , σ 2 ) ← (\sigma_1,\sigma_2) \qquad \leftarrow (σ1,σ2)←—————————————— ( g r , [ g x ⋅ ( g s k k ) ∑ j ∈ T k y j ] r ) (g^r,[g^x\cdot(g^{sk_k})^{\sum_{j\in\mathcal{T}_k}y^j}]^r) (gr,[gx⋅(gskk)∑j∈Tkyj]r)
(注意这是一组 { m i } i = 1 n \{m_i\}_{i=1}^n {mi}i=1n上的有效redacable签名,其中当 i ∈ T k , m i = s k k i\in\mathcal{T}_k,m_i=sk_k i∈Tk,mi=skk,否则等于0) -
用户运行 Σ . V e r i f y \Sigma.Verify Σ.Verify验证签名,
设 u s k k : = { s k k , ( σ 1 , σ 2 ) , T k } usk_k:=\{sk_k,(\sigma_1,\sigma_2),\mathcal{T}_k\} uskk:={skk,(σ1,σ2),Tk}-------------------------------------同时,管理员存储 ( g ~ s k k , T k ) → R e g [ k ] (\widetilde{g}^{sk_k},\mathcal{T}_k)\rightarrow{\rm Reg}[k] (g skk,Tk)→Reg[k]u s k k usk_k uskk中含有, s k k sk_k skk(相当于message m i m_i mi),范围 T k \mathcal{T}_k Tk(相当于 I \mathcal{I} I)和相应的签名。
− S i g n - {\rm Sign} −Sign:生成当前时间段内消息 m m m对应的签名
- 用户运行 Σ . D e r i v e ( p k , ( σ 1 , σ 2 ) , { m i } i = 1 n , { t } ) → σ I = ( σ 1 ′ , σ 2 ′ , σ 3 ′ , σ ~ ′ ) , I = { t } \Sigma.Derive(pk,(\sigma_1,\sigma_2),\{m_i\}_{i=1}^n,\{t\})\rightarrow \sigma_{\mathcal{I}}=(\sigma_1',\sigma_2',\sigma_3',\widetilde{\sigma}'),\mathcal{I}=\{t\} Σ.Derive(pk,(σ1,σ2),{mi}i=1n,{t})→σI=(σ1′,σ2′,σ3′,σ ′),I={t}, { m i } i = 1 n \{m_i\}_{i=1}^n {mi}i=1n定义同上
- 必须证明在message
m
t
=
s
k
k
≠
0
m_t=sk_k\neq 0
mt=skk=0上签名
σ
I
\sigma_{\mathcal{I}}
σI有效,由于
Σ
.
V
e
r
i
f
y
\Sigma.Verify
Σ.Verify的第二个等式只用
σ
I
\sigma_{\mathcal{I}}
σI的知识即可验证所以不用管;而第一个等式的验证需要
m
t
=
s
k
k
m_t=sk_k
mt=skk,(在redacable签名中验证知道需要的message,但在这里不能直接把私钥
s
k
k
sk_k
skk发给验证方),这意味着需要证明
s
k
k
sk_k
skk的知识:
e ( σ 1 , X ~ ⋅ σ ~ ⋅ Y ~ t s k k ) = e ( σ 2 , g ~ ) e(\sigma_1,\widetilde{X}\cdot\widetilde{\sigma}\cdot\widetilde{Y}_t^{sk_k})=e(\sigma_2,\widetilde{g})\\ e(σ1,X ⋅σ ⋅Y tskk)=e(σ2,g )
具体地,生成 a ← Z p a\leftarrow\mathbb{Z}_p a←Zp,计算 K = e ( σ 1 , Y ~ t ) a , c ← H ( K , σ I , m ) , s = a + c ⋅ s k k K=e(\sigma_1,\widetilde{Y}_t)^a,c\leftarrow H(K,\sigma_{\mathcal{I}},m),s=a+c\cdot sk_k K=e(σ1,Y t)a,c←H(K,σI,m),s=a+c⋅skk - 输出群签名 σ ← ( σ I , c , s ) \sigma\leftarrow(\sigma_{\mathcal{I}},c,s) σ←(σI,c,s)
−
R
e
v
o
k
e
- {\rm Revoke}
−Revoke.对每个用户
k
k
k在时间段
t
t
t上撤销,群管理员从
R
e
g
[
k
]
{\rm Reg}[k]
Reg[k]中恢复
g
~
s
k
k
\widetilde{g}^{sk_k}
g
skk,并将
(
g
~
s
k
k
)
y
t
(\widetilde{g}^{sk_k})^{y^t}
(g
skk)yt加入
R
L
t
{\rm RL}_t
RLt
−
V
e
r
i
f
y
(
g
p
k
,
t
,
R
L
t
,
σ
,
m
)
- {\rm Verify}(gpk,t,{\rm RL}_t,\sigma,m)
−Verify(gpk,t,RLt,σ,m).验证消息
m
m
m在时间段
t
t
t上的签名
σ
\sigma
σ
- 是否
Σ
.
V
e
r
i
f
y
\Sigma.Verify
Σ.Verify的第二个等式成立,即:
e ( σ 3 , g ~ ) = e ( Y n + 1 − t c t , σ ~ ) \begin{aligned} e(\sigma_3,\widetilde{g})&=e(Y_{n+1-t}^{c_t},\widetilde{\sigma})\\ \end{aligned} e(σ3,g )=e(Yn+1−tct,σ )
其中 c t ← H ( σ 1 ∣ ∣ σ 2 ∣ ∣ σ ~ ∣ ∣ { t } ∣ ∣ t ) c_t\leftarrow {\rm H}(\sigma_1||\sigma_2||\widetilde{\sigma}||\{t\}||t) ct←H(σ1∣∣σ2∣∣σ ∣∣{t}∣∣t) - 检查是否
m
t
=
0
m_t=0
mt=0,通过等式
e ( σ 1 , X ~ ⋅ σ ~ ) = e ( σ 2 , g ~ ) \begin{aligned} e(\sigma_1,\widetilde{X}\cdot \widetilde{\sigma})&=e(\sigma_2,\widetilde{g}) \end{aligned} e(σ1,X ⋅σ )=e(σ2,g )
等式成立,说明 m t = 0 m_t=0 mt=0,则返回0(推导如下)
e ( σ 2 , g ~ ) = e ( σ 1 , g ~ t + x + ∑ i = 1 n y i ⋅ m i ) = e ( σ 1 , g ~ x ⋅ g ~ t ⋅ ∏ j ∈ I ˉ Y ~ j m j ⋅ Y ~ t m t ) = e ( σ 1 , X ~ ⋅ σ ~ ⋅ Y ~ t m t ) \begin{aligned} e(\sigma_2,\widetilde{g})&=e(\sigma_1,\widetilde{g}^{t+x+\sum_{i=1}^ny^i\cdot m_i})\\ &=e(\sigma_1,\widetilde{g}^x\cdot\widetilde{g}^t\cdot\prod_{j\in\bar{\mathcal{I}}}\widetilde{Y}_j^{m_j}\cdot\widetilde{Y}_t^{m_t})\\ &=e(\sigma_1,\widetilde{X}\cdot\widetilde{\sigma}\cdot\widetilde{Y}_t^{m_t}) \end{aligned} e(σ2,g )=e(σ1,g t+x+∑i=1nyi⋅mi)=e(σ1,g x⋅g t⋅j∈Iˉ∏Y jmj⋅Y tmt)=e(σ1,X ⋅σ ⋅Y tmt) - 否则验证证明的知识:计算
K
′
K'
K′并验证
c
=
H
(
K
′
,
σ
I
,
m
)
c=H(K',\sigma_{\mathcal{I}},m)
c=H(K′,σI,m)
K ′ = e ( σ 1 , Y ~ t ) s ⋅ [ e ( σ 2 , g ~ ) ⋅ e ( σ 1 − 1 , X ~ ⋅ σ ~ ) ] − c = e ( σ 1 , Y ~ t ) a + c ⋅ s k k ⋅ [ e ( σ 1 , X ~ ⋅ σ ~ ⋅ Y ~ t s k k ) ⋅ e ( σ 1 − 1 , X ~ ⋅ σ ~ ) ] − c = e ( σ 1 , Y ~ t ) a + c ⋅ s k k ⋅ [ e ( σ 1 , X ~ ⋅ σ ~ ) ⋅ e ( σ 1 , Y ~ t s k k ) ⋅ e ( σ 1 − 1 , X ~ ⋅ σ ~ ) ] − c = e ( σ 1 , Y ~ t ) a = K \begin{aligned} K'&=e(\sigma_1,\widetilde{Y}_t)^s\cdot[e(\sigma_2,\widetilde{g})\cdot e(\sigma_1^{-1},\widetilde{X}\cdot\widetilde{\sigma})]^{-c}\\ &=e(\sigma_1,\widetilde{Y}_t)^{a+c\cdot sk_k}\cdot[e(\sigma_1,\widetilde{X}\cdot\widetilde{\sigma}\cdot\widetilde{Y}_t^{sk_k})\cdot e(\sigma_1^{-1},\widetilde{X}\cdot\widetilde{\sigma})]^{-c}\\ &=e(\sigma_1,\widetilde{Y}_t)^{a+c\cdot sk_k}\cdot[e(\sigma_1,\widetilde{X}\cdot\widetilde{\sigma})\cdot e(\sigma_1,\widetilde{Y}_t^{sk_k})\cdot e(\sigma_1^{-1},\widetilde{X}\cdot\widetilde{\sigma})]^{-c}\\ &=e(\sigma_1,\widetilde{Y}_t)^{a}=K \end{aligned} K′=e(σ1,Y t)s⋅[e(σ2,g )⋅e(σ1−1,X ⋅σ )]−c=e(σ1,Y t)a+c⋅skk⋅[e(σ1,X ⋅σ ⋅Y tskk)⋅e(σ1−1,X ⋅σ )]−c=e(σ1,Y t)a+c⋅skk⋅[e(σ1,X ⋅σ )⋅e(σ1,Y tskk)⋅e(σ1−1,X ⋅σ )]−c=e(σ1,Y t)a=K
以上推导成立的前提是 Σ . V e r i f y \Sigma.Verify Σ.Verify算法的第一项等式成立. - 以上验证通过说明
σ
\sigma
σ是一个有效的签名,但它有可能是由已经撤销的密钥签署的。对于每个
h
~
k
∈
R
L
t
\widetilde{h}_k\in{\rm RL}_t
h
k∈RLt,算法检查是否
e
(
σ
1
,
h
~
k
)
=
e
(
σ
2
,
g
~
)
⋅
e
(
σ
1
−
1
,
X
~
⋅
σ
~
)
e(\sigma_1,\widetilde{h}_k)=e(\sigma_2,\widetilde{g})\cdot e(\sigma_1^{-1},\widetilde{X}\cdot \widetilde{\sigma})
e(σ1,h
k)=e(σ2,g
)⋅e(σ1−1,X
⋅σ
)
已知
e ( σ 1 , h ~ k ) = e ( σ 1 , ( g ~ s k k ) y t ) e(\sigma_1,\widetilde{h}_k)=e(\sigma_1,(\widetilde{g}^{sk_k})^{y^t}) e(σ1,h k)=e(σ1,(g skk)yt)
检查:
e ( σ 2 , g ~ ) ⋅ e ( σ 1 − 1 , X ~ ⋅ σ ~ ) = e ( σ 1 , X ~ ⋅ σ ~ ⋅ Y ~ t s k k ) ⋅ e ( σ 1 − 1 , X ~ ⋅ σ ~ ) = e ( σ 1 , Y ~ t s k k ) ⋅ e ( σ 1 , X ~ ⋅ σ ~ ) ⋅ e ( σ 1 − 1 , X ~ ⋅ σ ~ ) = e ( σ 1 , Y ~ t s k k ) = e ( σ 1 , h ~ k ) \begin{aligned} e(\sigma_2,\widetilde{g})\cdot e(\sigma_1^{-1},\widetilde{X}\cdot \widetilde{\sigma})&=e(\sigma_1,\widetilde{X}\cdot\widetilde{\sigma}\cdot\widetilde{Y}_t^{sk_k})\cdot e(\sigma_1^{-1},\widetilde{X}\cdot \widetilde{\sigma})\\ &=e(\sigma_1,\widetilde{Y}_t^{sk_k})\cdot e(\sigma_1,\widetilde{X}\cdot\widetilde{\sigma})\cdot e(\sigma_1^{-1},\widetilde{X}\cdot \widetilde{\sigma})\\ &=e(\sigma_1,\widetilde{Y}_t^{sk_k})=e(\sigma_1,\widetilde{h}_k) \end{aligned} e(σ2,g )⋅e(σ1−1,X ⋅σ )=e(σ1,X ⋅σ ⋅Y tskk)⋅e(σ1−1,X ⋅σ )=e(σ1,Y tskk)⋅e(σ1,X ⋅σ )⋅e(σ1−1,X ⋅σ )=e(σ1,Y tskk)=e(σ1,h k)
成立的前提还是 Σ . V e r i f y \Sigma.Verify Σ.Verify算法的第一项等式成立,且对应的 s k k sk_k skk在时间段 t t t已被撤销。成立则返回0,否则返回1.
− O p e n ( g s k , R e g , σ , m , t ) → k / ⊥ - {\rm Open}(gsk,{\rm Reg},\sigma,m,t)\rightarrow k/\perp −Open(gsk,Reg,σ,m,t)→k/⊥对于每个在时间 t t t内活跃的用户 k k k,这个算法从 R e g [ k ] {\rm Reg}[k] Reg[k]中恢复 g ~ s k k \widetilde{g}^{sk_k} g skk,并测试: e ( σ 1 , g ~ s k k ) = [ e ( σ 2 , g ~ ) ⋅ e ( σ 1 − 1 , X ~ ⋅ σ ~ ) ] y − t e\left(\sigma_{1}, \widetilde{g}^{\mathbf{s k}_{k}}\right)=\left[e\left(\sigma_{2}, \widetilde{g}\right) \cdot e\left(\sigma_{1}^{-1}, \widetilde{X} \cdot \widetilde{\sigma}\right)\right]^{y^{-t}} e(σ1,g skk)=[e(σ2,g )⋅e(σ1−1,X ⋅σ )]y−t
可看出这个条件与Verify中验证撤销密钥的条件几乎相同(仅将 y t y^t yt消去),通过遍历 R e g {\rm Reg} Reg中的元素,测试直到找到符合这个签名的 g ~ s k k \widetilde{g}^{sk_k} g skk对应的index k k k(注意只有拥有 g s k : y gsk:y gsk:y的人才能打开签名)
Efficiency
Redactable Signature
(
G
1
:
382
b
i
t
s
G
2
:
763
b
i
t
s
≈
2
G
1
\mathbb{G}_1:382{\rm bits}~\mathbb{G}_2:763{\rm bits}\approx2\mathbb{G}_1
G1:382bits G2:763bits≈2G1,
r
i
r_i
ri表示
G
i
\mathbb{G}_i
Gi中随机元素的生成,
e
i
e_i
ei表示
G
i
\mathbb{G}_i
Gi上的指数计算)

p
k
:
(
H
,
g
∈
G
1
∗
,
g
~
∈
G
2
∗
,
{
Y
i
}
i
=
1
n
,
{
Y
i
}
i
=
n
+
2
2
n
,
X
~
,
{
Y
~
i
}
i
=
1
n
)
:
(
1
+
2
n
−
1
)
G
1
+
(
n
+
2
)
G
2
=
382
(
4
n
+
4
)
b
i
t
s
pk:(H,g\in\mathbb{G}_1^*,\widetilde{g}\in\mathbb{G}_2^*,\{Y_i\}_{i=1}^n,\{Y_i\}_{i=n+2}^{2n},\widetilde{X},\{\widetilde{Y}_i\}_{i=1}^n):(1+2n-1)\mathbb{G}_1+(n+2)\mathbb{G}_2=382(4n+4){\rm bits}
pk:(H,g∈G1∗,g
∈G2∗,{Yi}i=1n,{Yi}i=n+22n,X
,{Y
i}i=1n):(1+2n−1)G1+(n+2)G2=382(4n+4)bits
σ
:
(
σ
1
∈
G
1
,
σ
2
∈
G
1
,
σ
3
∈
G
1
,
σ
~
∈
G
2
)
:
3
G
1
+
1
G
2
=
382
×
3
+
763
=
1909
b
i
t
s
\sigma:(\sigma_1\in\mathbb{G}_1,\sigma_2\in\mathbb{G}_1,\sigma_3\in\mathbb{G}_1,\widetilde{\sigma}\in\mathbb{G}_2):3\mathbb{G}_1+1\mathbb{G}_2=382\times3+763=1909{\rm bits}
σ:(σ1∈G1,σ2∈G1,σ3∈G1,σ
∈G2):3G1+1G2=382×3+763=1909bits
S
i
g
n
Sign
Sign:1个随机元素
σ
1
∈
G
1
\sigma_1\in\mathbb{G}_1
σ1∈G1,1次
∈
G
1
\in\mathbb{G}_1
∈G1上的指数计算
D
e
r
i
v
e
Derive
Derive:
3
+
(
2
n
−
1
)
3+(2n-1)
3+(2n−1)次
G
1
\mathbb{G}_1
G1指数计算(
σ
3
\sigma_3
σ3用改进的方法生成),
1
+
(
n
−
k
)
1+(n-k)
1+(n−k)次
G
2
\mathbb{G}_2
G2指数计算,
k
k
k次hash
V
e
r
i
f
y
Verify
Verify:
k
k
k次
G
2
\mathbb{G}_2
G2指数计算,
k
k
k次
G
1
\mathbb{G}_1
G1指数计算,
k
k
k次hash,
2
2
2个包含
2
2
2个双线性对计算的等式。
Group Signature with Time-Bound Keys

p
k
pk
pk与Redactable Signature相同
u
s
k
k
=
{
s
k
k
∈
Z
p
,
(
σ
1
,
σ
2
)
∈
G
1
2
,
T
k
}
:
2
G
1
+
1
Z
p
=
382
×
2
+
256
usk_k=\{sk_k\in\mathbb{Z}_p,(\sigma_1,\sigma_2)\in\mathbb{G}_1^2,\mathcal{T}_k\}:2\mathbb{G}_1+1\mathbb{Z}_p=382\times 2+256
uskk={skk∈Zp,(σ1,σ2)∈G12,Tk}:2G1+1Zp=382×2+256
R
L
{\rm RL}
RL中的元素形式:
(
g
~
s
k
k
)
y
t
(\widetilde{g}^{sk_k})^{y^t}
(g
skk)yt:
R
G
2
=
763
R
b
i
t
s
R\mathbb{G}_2=763R~{\rm bits}
RG2=763R bits
σ
←
(
σ
I
,
c
,
s
)
=
(
3
G
1
+
1
G
2
,
Z
p
,
Z
p
)
:
382
×
3
+
763
+
256
×
2
=
2421
b
i
t
s
\sigma\leftarrow(\sigma_{\mathcal{I}},c,s)=(3\mathbb{G}_1+1\mathbb{G}_2,\mathbb{Z}_p,\mathbb{Z}_p):382\times 3+763+256\times 2=2421{\rm bits}
σ←(σI,c,s)=(3G1+1G2,Zp,Zp):382×3+763+256×2=2421bits
计算复杂度

S
i
g
n
:
n
=
2
,
k
=
1
Sign:n=2,k=1
Sign:n=2,k=1,原本
Σ
.
D
e
r
i
v
e
\Sigma.Derive
Σ.Derive的复杂度为:
6
e
1
+
H
+
2
e
2
6e_1+H+2e_2
6e1+H+2e2,签名引入:
p
1
+
H
p_1+H
p1+H
V
e
r
i
f
y
:
Verify:
Verify:算不对…
总结
redactable 签名:
- 使用原签名的一个特例 y i → y i y_i\rightarrow y^i yi→yi,私钥简化
- 提出新的安全性验证条件,所需公钥由二次简化为一次。
- 保持了原签名中的不可链接性原理
用redactable 签名实现的满足时间限制密钥的群签名:
- 用redactable 签名生成一个总签名,这里总集是 T k \mathcal{T}_k Tk, s k k sk_k skk在签名中作为message,私钥和总签名共同作为用户签名私钥
- 签名生成时,运行 D e r i v e Derive Derive派生出 T k \mathcal{T}_k Tk的子集 { t } \{t\} {t}上的签名, c c c是非交互挑战, s s s是返回值,构造这个的目的是证明向验证方证明 s k k sk_k skk的知识(因为作为message的 s k k sk_k skk不能被直接发给验证方)。
- 撤销设置:将与 s k k sk_k skk和 t t t有关的一个计算结果提交到撤销集合,表示撤销 k k k在 t t t上的权限
- 验证redactable 签名的验证条件2通过; m t ≠ 0 m_t\neq 0 mt=0即对应的 s k k sk_k skk不是0;验证redactable 签名的验证条件1通过; t t t未被撤销
- 从签名和 t t t中返回 k k k






















 1786
1786











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








