非线性系统学习笔记：2，向量场、相图以及向量场箭头大小一致的实现。

最新推荐文章于 2024-02-05 18:45:00 发布

风起岭之南

最新推荐文章于 2024-02-05 18:45:00 发布

阅读量789

点赞数 3

文章标签：学习 matlab

本文链接：https://blog.csdn.net/jiu_zuo_jiu_die/article/details/134693443

版权

一个由两个常微分方程表示的二阶自洽系统：

$\dot{x_{1}} =f_{1}(x_{1},x_{2})\\ \dot{x_{2}} =f_{2}(x_{1},x_{2})$

设 $x(t) = (x_{1}(t),x_{2}(t))$ 是系统的解函数。

初始条件：

$x(0) = x_{0}=(x_{10},x_{20})$

平面 $x_{1}-x_{2}$ 被称为相平面。

可以使用向量的形式表示该二阶自洽系统：

$\dot{x}=f(x)$

为了可视化方便，在相平面上，画出f(x)，形成的图像叫做该系统的向量场。

以下是一个点的向量画法：

以点x=(1,1)为例，

假设:

$f(x)=(2x_{1}^{2},x_{2})$

则有：

x+f(x)=(1,1)+(2,1)=(3,2)

用箭头从(1,1)指向(3,2)，表示该点的向量。

向量的长度

$\sqrt{f_{1}^{2}(x)+f_{2}^{2}(x)}$

不断重复以上操作，对所有的点，都画出其向量。

构造轨迹线：

从初始点x0开始，沿着与x0向量相切的方向到达下一个点，一直重复这个操作，如果这些点是连续的点（或者是点与点之间离的足够近），那么行进的轨迹就是一条曲线，如果其终点还是x0，说明这是一条闭合的曲线，闭合的曲线说明了该系统存在周期解，也就是说该系统会有一个持续的振荡（如果轨迹线是螺旋收缩的，那么系统会有一个衰减的振荡）。

不同的初始点，就会得到不同的轨迹线。在x1-x2相平面上，画出所有的初始条件下的轨迹线，这些轨迹线构成了系统的相图。相图是变量与变量导数的轨迹图（横轴为变量，纵轴为该变量的导数）。

相图中，没有体现时间，因此通过相图是不能够定量的体现轨迹线对应的解（x1(t)，x2(t)），只能进行定性分析。

例子：以书中隧道二极管电路为例。

$\dot{x_{1}}=0.5[-h(x)+x_{2}]\\\dot{x_{2}}=0.2(-x_{1}-1.5x_{2}+1.2)\\ h(x_{1})=17.76x_{1}-103.79x_{1}^{2}+229.62x_{1}^{3}-226.31x_{1}^{4}+83.72x_{1}^{5}$

代码：

figure("name", "轨迹图")
[y,dy]=meshgrid(-0.5:0.02:1.5,-0.5:0.02:1.5);%初始化网格
u=0.5.*(-17.76.*y+103.79.*y.^2-229.62.*y.^3+226.31.*y.^4-83.72.*y.^5+dy);
v=0.2.*(-y-1.5.*dy+1.2);
streamslice(y,dy,u,v, 1)
xlabel('x1')
ylabel('x2')
hold on;
figure("name", "向量场")
[y,dy]=meshgrid(-0.5:0.05:1.5,-0.5:0.05:1.5);%初始化网格
u=0.5.*(-17.76.*y+103.79.*y.^2-229.62.*y.^3+226.31.*y.^4-83.72.*y.^5+dy);
v=0.2.*(-y-1.5.*dy+1.2);
q=quiver(y,dy,u,v);
xlabel('x1')
ylabel('x2')
hold on

结果：

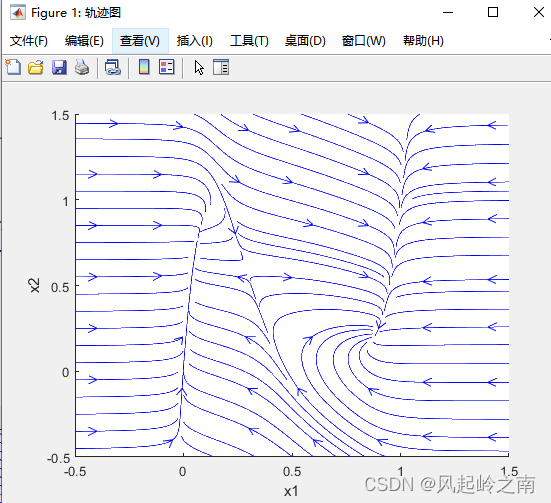
发现使用Matlab画向量场时，其箭头的大小是会自动缩放的，在视觉上，是不够清晰的。当然，quiver函数是提供一些参数，对箭头进行调整的，但是想要箭头的大小一致的话，是无法通过调整参数去实现的。

那么如何实现箭头大小一致的向量场呢？

matlab绘制用颜色表示模值大小的箭头图

需要自己定义自己的自适应缩放系数。

代码接上：

%求模：向量长度。
M = sqrt(u.^2 + v.^2);
%求最大的长度，作为标准。
up = max(M(:));
%自适应缩放因子
scaler1 = up./M;
%分别对水平分量和垂直分量进行缩放。
%a为各自系统的调整因子，不同系统，调整因子不一样；
%可以通过不断的尝试，找出比较适合的调整因子。
a = 0.0011;
u = u.*scaler1.*a;
v = v.*scaler1.*a;
figure("name", "箭头一致的向量场")
[m,n] = size(y);
for i=1:m
    for j=1:n
        %MaxHeadSize为箭头头部的最大大小。默认值为0.5.
        quiver(y(i,j),dy(i,j),u(i,j),v(i,j),"MaxHeadSize", 10);
        hold on
    end 
end
hold on

结果：

视觉效果很不错。